【论文分享】MAD-GAN :基于生成对抗网络的时间序列数据多元异常检测
2019年ICANN文章
MAD-GAN: Multivariate Anomaly Detection for Time Series Data
with Generative Adversarial Networks
Dan Li1, Dacheng Chen1, Lei Shi1, Baihong Jin2, Jonathan Goh3, and See-Kiong Ng1
- 无监督学习
这GAN网络的一次全新的尝试,无论是检测模块还是训练模块中,GAN网络的基础框架都是用LSTM-RNN来捕获时间序列分布的时间相关性,原文中提出了一个新的异常评分——DR评分并贡献了两个数据集
摘要
网络化传感器和执行器在许多现实系统中的普及,例如智能系统建筑物、工厂、发电厂和数据中心这些系统生成大量的多元时间序列数据。许多这样的网络物理系统(cps)是为关键任务而设计的,因此是网络攻击的目标。丰富的传感器数据可以通过异常检测持续监控入侵事件。然而,由于这些系统的动态复杂性,传统的基于阈值的异常检测方法是不够的,而有监督的机器学习方法由于缺乏标记数据而无法利用大量的数据。另一方面,目前的无监督机器学习方法还没有充分利用系统中多变量(传感器/执行器)之间的时空相关性和其他依赖性来检测异常。目前的大多数技术还采用简单的比较当前状态和预测的正常范围来进行异常检测,考虑到系统的高度动态行为,这是不够的。
在这项工作中,我们提出了一种基于生成性对抗网络(GANs)的无监督多元异常检测方法,在GAN框架中使用长-短期记忆递归神经网络(LSTM-RNN)作为基本模型(即生成器和鉴别器)来捕获时间序列分布的时间相关性。我们提出的多元异常检测框架(MAD-GAN)没有独立地处理每个数据流,而是同时考虑整个变量集,以捕捉变量之间潜在的相互作用。我们还充分利用了GAN产生的生成器和判别器,使用了一种新的异常评分DR-score,通过判别和分析来检测异常重建。我们已经使用从真实世界CPS收集的两个最新数据集测试了我们提出的MAD-GAN:安全水处理(SWaT)和水分配(WADI)数据集。我们的实验结果表明,与这些复杂的现实系统相比,MAD-GAN在报告各种网络入侵引起的异常方面是有效的。
关键词:异常检测,多元时间序列,网络入侵,生成对抗网络(GAN)。
引言
当今的网络物理系统(CPS),如智能建筑、工厂、发电厂和数据中心,都是大型的、复杂的,并配有网络传感器和执行器,这些传感器和执行器产生大量的多元时间序列数据,可用于连续监测CPS的工作状况,及时发现异常情况,以便操作员采取行动调查和解决根本问题。随着物联网(IoT)的出现,网络化传感器和执行器在CPS和其他系统(如自动车辆)中的普遍使用将变得更加普遍,导致多个系统和设备通过网络进行通信,并可能自主地操作大量任务。由于许多CPS是为关键任务设计的,它们是网络攻击的主要目标。因此,利用这些系统产生的多变量时间序列数据,通过异常检测来密切监视这些系统的行为,以防止入侵事件的发生,显得尤为重要。
异常通常被定义为在某些时间步长中系统的行为与之前的正常状态显着不同的点 [2]。 因此,异常检测的基本任务是识别异常可能发生的时间步长。 传统上,统计过程控制 (SPC) 方法(例如 CUSUM、EWMA 和休哈特图)是用于监控工业过程质量以找出超出范围的工作状态的流行解决方案 [3]。这些传统的检测技术无法处理由现代 CPS 日益动态和复杂的性质产生的多变量数据流。 因此,研究人员已经超越了基于规范或签名的技术,并开始利用机器学习技术来利用系统生成的大量数据[4]。由于标记数据的固有缺乏,异常检测通常被视为无监督的机器学习任务。 然而,大多数现有的无监督方法是通过线性投影和变换构建的,无法处理多元时间序列隐藏的固有相关性中的非线性。 此外,大多数当前技术采用当前状态和预测的正常范围之间的简单比较来检测异常情况,鉴于系统的高度动态特性,这可能是不够的。
最近,已经提出了生成对抗网络 (GAN) 框架通过对抗训练来构建生成深度学习模型 [5]。 虽然 GAN 已被证明在图像处理任务(例如生成逼真的图像)方面取得了巨大成功,但迄今为止在将 GAN 框架用于时间序列数据方面的工作还很有限。 据我们所知,文献中使用 GAN 生成连续值序列的初步工作很少。然而,在这些早期工作中,GAN 框架已被证明在生成时间序列序列方面是有效的,要么使用循环神经网络作为生成器和鉴别器生成复调音乐 [6],要么使用条件生成实值医学时间序列 循环 GAN [7] 的版本。 GAN 在生成逼真的复杂数据集方面的这些早期成功,以及以对抗方式同时训练生成器和判别器,高度暗示使用 GAN 框架进行异常检测。
在这项工作中,我们提出了一种新的带有 GAN 的多元异常检测策略(MAD-GAN)来模拟多个数据流之间复杂的多元相关性,以使用 GAN 训练的生成器和鉴别器来检测异常。 与传统的分类方法不同,GAN 训练的鉴别器学习以无监督的方式从真实数据中检测假数据,使其成为一种有吸引力的异常检测无监督机器学习技术 [8]。 受 [9] 和 [10] 的启发,更新从实时空间到某个潜在空间的映射以增强生成器和鉴别器的训练,研究人员最近提出训练一个潜在空间可理解的 GAN 并将其应用于任意数据分布的丰富特征表示的无监督学习。[11] 和 [12] 展示了使用来自潜在空间的重建测试样本识别异常的可能性,并成功地应用了所提出的基于 GAN 的检测策略来发现图像的意外标记。 在这项工作中,我们将利用这些以前的工作,利用 GAN 训练的生成器和鉴别器来检测基于重建和鉴别损失的异常。
本文的其余部分安排如下。 第 2 节概述了相关工作。 第 3 节介绍了我们提出的 MAD-GAN 框架和异常评分函数。 在第 6 节中,我们介绍了经过测试的 CPS 和数据集。 在第 5 节中,我们展示了我们提出的 MAD-GAN 在两个真实 CPS 数据集上的实验结果。 最后,第 6 节总结了整篇论文并提出了未来可能的工作。
2 相关工作
鉴于用于训练监督算法的标记异常数据的固有缺乏,异常检测方法主要基于无监督方法。 我们可以将无监督检测方法分为四类:i)基于线性模型的方法,ii)基于距离的方法,iii)基于概率和密度估计的方法,以及 vi)最近非常流行的基于深度学习的方法 。
对于基于线性模型的无监督异常检测方法,一种流行的方法是主成分分析 (PCA) [13]。 PCA 基本上是一种多元数据分析方法,它保留了从过程测量中提取的显着可变性信息,并减少了大量相关数据的维度 [14]。 PLS 是另一种多元数据分析方法,已广泛用于模型构建和异常检测 [15]。 然而,它们只对高度相关的数据有效,并且要求数据遵循多元高斯分布[16]。
对于基于距离的方法,一种流行的方法是 K-最近邻 (KNN) 算法,该算法计算与其 k 个最近邻的平均距离,并基于该距离获得异常分数 [17]。 基于聚类的局部异常值因子 (CBLOF) 方法是基于距离的方法的另一个示例。 它使用预定义的异常评分函数来识别基于聚类的异常,这是局部异常因子 (LOF) 方法的增强版本 [18]。 尽管在某些情况下有效,但这些基于距离的方法在异常持续时间和异常数量的先验知识下表现更好。
通过更加关注数据分布,提出了基于概率模型和基于密度估计的方法作为基于距离方法的改进。 例如,基于角度的异常值检测 (ABOD) 方法 [19] 和特征装袋 (FB) 方法 [20] 通过考虑变量相关性来处理数据。 然而,这些方法无法考虑时间步长的时间相关性,因此不适用于多元时间序列数据。
基于深度学习的无监督异常检测方法最近因其良好的性能而广受欢迎。 例如,自动编码器 (AE) [21] 是一种流行的深度学习模型,通过检查其重建错误来进行异常检测。 其他如深度自动编码高斯混合模型 (DAGMM) [22] 和 LSTM 编码器-解码器 [23] 也报告了多变量异常检测的良好性能。 在这项工作中,我们遵循基于深度学习的无监督异常检测方法的成功,并提出了一种基于生成对抗网络 (GAN) 的新型基于深度学习的无监督异常检测策略。
我们对本文的贡献总结如下:(i)我们提出了 MAD-GAN,一种基于 GAN 的无监督异常检测方法,用于检测多元时间序列的异常; (ii) MAD-GAN 架构采用之前为图像相关应用开发的 GAN 框架,通过采用长短期循环神经网络 (LSTM-RNN) 作为 GAN 学习的基础模型来分析多元时间序列数据 时间依赖性; (iii) 我们使用 GAN 的鉴别器和生成器来检测异常,使用新的异常分数来检测异常,该分数结合了每个测试样本的鉴别结果和重建残差。 所提出的 MAD-GAN 在检测由两个 CPS 数据集的网络攻击引起的异常方面优于现有方法。
3 使用生成对抗训练进行异常检测
时间序列异常检测的基本任务是识别测试数据是否符合正态数据分布; 不合格点在各种应用领域被称为异常、异常值、入侵、故障或污染物 [4]。 图 1 描绘了所提出的 MAD-GAN 的整体架构。
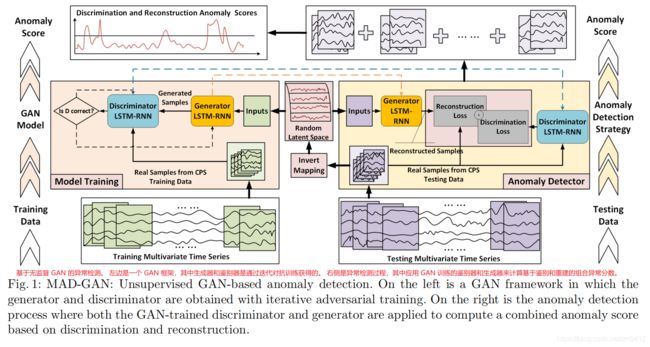
3.1 MAD-GAN架构
首先,为了处理时间序列数据,我们将 GAN 的生成器和鉴别器构建为两个长短期循环神经网络 (LSTM-RNN),如图 1 左中部分所示。遵循典型的 GAN 框架 , 生成器 (G) 以来自随机潜在空间的序列作为其输入生成假时间序列,并将生成的序列样本传递给鉴别器 (D),后者将尝试区分生成的(即“假”)数据序列与 实际(即“真实”)正常训练数据序列。
MAD-GAN 框架不是独立处理每个数据流,而是同时考虑整个变量集,以便将变量之间的潜在交互捕获到模型中。 在区分之前,我们将多元时间序列划分为带有滑动窗口的子序列。 为了凭经验确定子序列表示的最佳窗口长度,我们使用不同的窗口大小来捕获不同分辨率下的系统状态,即 sw = 30 × i, i = 1, 2, …, 10。
与标准 GAN 框架一样,D 和 G 的参数根据 D 的输出进行更新,因此可以训练鉴别器尽可能灵敏地为真实和虚假序列分配正确的标签,而生成器将 经过足够轮次的迭代后,训练为尽可能聪明地欺骗鉴别器(即误导 D 将真实标签分配给假序列)。通过能够生成真实样本,生成器 G 将捕获训练序列的隐藏多元分布,并且可以将其视为系统在正常状态下的隐式模型。 同时,由此产生的鉴别器 D 也经过训练,能够以高灵敏度区分虚假(即异常)数据和真实(即正常)数据。 在这项工作中,我们建议通过(i)重建利用 G 和 D 进行异常检测任务:基于从实时空间到 GAN 潜在的映射,利用 G 的实时测试样本和重建样本之间的残差 空间; (ii) 判别:使用判别器 D 对时间序列进行分类。 这在图 1 的右中间部分进行了描述。如图所示,测试样本被映射回潜在空间,以根据重建的测试样本(由生成器 G)和实际测试样本之间的差异计算相应的重建损失。 同时,测试样本也被馈送到训练好的判别器 D 来计算判别损失。 请注意,测试多元时间序列类似地通过滑动窗口划分为一组子序列,然后再输入检测模型。 我们使用一种新颖的判别和重建异常分数(DR-Score)来结合这两种损失来检测数据中的潜在异常(更多细节在第 3.3 节中描述)。
3.2 基于 GAN 的异常检测
现在让我们用 GAN 来表述异常检测问题。 给定一个训练数据集 X ⊆ R M × T X ⊆ R^{M×T} X⊆RM×T,每个流有 T 个流和 M 个测量值,以及一个测试数据集 X t e s t ⊆ R N × T X^{test} ⊆ R^{N×T} Xtest⊆RN×T,每个流有 T 个流和 N 个测量值,任务是分配二进制(0 表示正常和 1 表示异常) 标签到测试数据集的测量值。 请注意,我们在这里假设训练数据集中的所有点都是正常的。
为了有效地从 X 中学习,我们应用了一个窗口大小为 s w s_w sw 和步长为 s s s_s ss 的滑动窗口来将多元时间序列划分为一组多元子序列 X = { x i x_i xi , i = 1, 2, …, m} ⊆ R^{s_w×T},其中 m = ( M − s w ) / s s m =(M−s_w) /s_s m=(M−sw)/ss 是子序列的数量。 类似地,Z = { z i z_i zi , i = 1, 2, …, m} 是一组从随机空间中提取的多元子序列。 通过将 X 和 Z 提供给 GAN 模型,我们使用以下两人极小极大博弈训练生成器和鉴别器:
![]()
在这项工作中,GAN 的生成器 (G) 和鉴别器 (D) 都是长短期循环神经网络 (LSTM-RNN)。 经过足够轮次的训练迭代后,可以使用经过训练的判别器 D r n n D_{rnn} Drnn 和生成器 G r n n G_{rnn} Grnn 使用组合的判别和重建异常分数(DR-Score)来检测 X t e s t X^{test} Xtest中的异常,这将在第 3.3 节中介绍。
对于检测,测试数据集 X t e s t ⊆ R N × T X^{test} ⊆ R^{N×T} Xtest⊆RN×T 类似地划分为具有滑动窗口的多元子序列 X t e s = x j t e s X^{tes} = x^{tes}_j Xtes=xjtes ,j = 1, 2, …, n ,其中 n = ( N − s w ) / s s n = (N−s_w)/s_s n=(N−sw)/ss 。 使用测试数据集的计算出的 DR-Score (DRS),我们将测试数据集中的每个子序列标记如下:
![]()
其中 A t t e s ⊆ R N × 1 A^{tes}_t ⊆ R^{N×1} Attes⊆RN×1 是测试数据集的标签向量,其中非零值表示检测到异常,即异常分数的交叉熵误差 H (., .) 高于预定义值 τ \tau τ。
3.3 DR-Score:使用判别和重建进行异常检测
使用 GAN 的一个优势是我们将同时训练一个鉴别器和一个生成器。 我们建议利用经过联合训练的鉴别器和生成器来表示正常的解剖变异,以识别异常。 遵循 [11] 中的公式,基于 GAN 的异常检测由以下两部分组成:
1. 基于判别的异常检测
鉴于训练有素的鉴别器 D 可以高灵敏度地将虚假数据(即异常)与真实数据区分开来,它可以作为异常检测的直接工具。
2. 基于重构的异常检测
经过训练的生成器 G,能够生成真实样本,实际上是一个从隐空间到真实数据空间的映射:G(Z) : Z → X,可以看作是一个反映正态分布的隐式系统模型数据的分布。 由于 [24] 中提到的潜在空间的平滑过渡,如果潜在空间中的输入接近,生成器会输出相似的样本。因此,如果有可能在潜在空间中为测试数据 X t e s X^{tes} Xtes 找到对应的 Z k Z^k Zk,则 X t e s X^{tes} Xtes 与 G ( Z k ) G(Z^k) G(Zk)(即重构的测试样本)之间的相似性可以解释 X t e s X^{tes} Xtes 在多大程度上遵循由下式反映的分布 G. 换句话说,我们还可以使用 X t e s X^{tes} Xtes 和 G ( Z k ) G(Z^k) G(Zk) 之间的残差来识别测试数据中的异常。
为了找到与测试样本相对应的最优 Z k Z^k Zk,我们首先从潜在空间中采样一个随机集 Z 1 Z^1 Z1,并通过将其馈送到生成器来获得重建的原始样本 G ( Z 1 ) G(Z^1) G(Z1)(如图 1 的右侧部分所示)。然后,我们使用从 X t e s X^{tes} Xtes 和 G ( Z ) G(Z) G(Z) 定义的误差函数获得的梯度更新潜在空间中的样本。为简单起见,序列之间的相似性可以定义为协方差。
![]()
经过足够多的迭代轮次使得误差足够小,样本 Z k Z^k Zk 被记录为相应的测试样本的潜在空间中的映射。 测试样本在时间 t 的残差计算为
![]()
其中 X t t e s ⊆ R n X_t^{tes} ⊆ R^n Xttes⊆Rn 是 n 个变量在时间步长 t 的测量值。 换句话说,异常检测损失为
![]()
基于以上描述,GAN 训练的判别器和生成器对于每个测试数据子序列会输出一组异常检测损失 { L = L j , s , j = 1 , 2 , . . . , n ; s = 1 , 2 , . . . , s w L = L_{j,s}, j = 1, 2, ..., n; s = 1, 2, ..., s_w L=Lj,s,j=1,2,...,n;s=1,2,...,sw} ⊆ R n × s w ⊆ R^{n×s_w} ⊆Rn×sw。 我们通过将子序列的异常检测损失映射回原始时间序列来计算称为 DR-Score (DRS) 的组合歧视和重建异常分数:
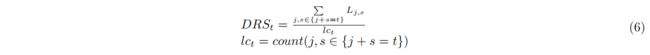
其中 t t t ∈ {1, 2, …, N N N}, j j j ∈ {1, 2, …, n n n}, and s s s ∈ {1, 2, …, s w s_w sw}
提出的 MAD-GAN 在 Algo1 中进行了总结。 我们使用基于 Adam Optimizer 和 Gradient Descent Optimizer 的小批量随机优化来更新这项工作中的模型参数。

4 CPSs and Cyber-attacks(CPS 和网络攻击)
4.1 水处理和分配系统
4.1.1 SWaT
安全水处理 (SWaT) 系统是水处理的操作试验台,它代表了大城市中大型现代水处理厂的小规模版本 [25]。 整体试验台设计与新加坡公共事业委员会(全国性的水务公司)协调,以确保整个物理过程和控制系统与现场的真实系统非常相似。 SWaT 数据集收集过程持续了 11 天,系统每天 24 小时运行。 在 2016 年 SWaT 数据收集过程的最后 4 天,总共发起了 36 次攻击 [26]。通常,攻击点包括传感器(如水位传感器、流量计等)和执行器(如阀门、泵等)。 在最后四天,这些攻击以不同的意图和不同的持续时间(从几分钟到一个小时)在测试台上发起。 系统要么被允许在发起另一次攻击之前达到其正常运行状态,要么连续发起攻击。 有关 SWaT 数据集的更多详细信息,请参阅 SWat 网站4。
SWaT 中的水净化过程由六个子过程组成,称为 P1 到 P6 [26]。 第一个过程是原水的供应和储存,P2 是用于评估水质的预处理。 不需要的材料在 P3 中通过超滤 (UF) 反洗去除。 剩余的氯在脱氯过程 (P4) 中被破坏。 随后,来自 P4 的水被泵入反渗透 (RO) 系统 (P5) 以减少无机杂质。 最后,P6 存储准备分配的水。
4.1.2 WADI
与通常包含在安全位置的水处理系统工厂不同,分配系统包括跨越大面积的众多管道。 这极大地增加了对配电网络进行物理攻击的风险。 配水 (WADI) 试验台是 SWaT 系统的扩展,通过吸收部分 SWaT 反渗透渗透水和原水,形成完整且真实的水处理、储存和分配网络。配水系统共有三个控制过程。 第一个过程是从 SWaT、公共事业委员会 (PUB) 入口或 WADI 的回水取水,并将原水储存在两个水箱中。 P2 根据预设的需求模式分配来自两个高架蓄水池和六个消费者水箱的水。 水在第三道工序中被回收并送回 P1。
WADI 试验台同样配备了化学计量系统、增压泵和阀门、仪器仪表和分析仪 [27]。 除了通过网络模拟对 PLC 进行的攻击和防御之外,WADI 还能够模拟物理攻击的影响,例如漏水和恶意化学品注入。 WADI 数据采集过程包括 16 天的连续运行,其中 14 天是在正常运行情况下采集的数据,2 天是在攻击场景下采集的。 在数据收集期间,收集了所有网络流量、传感器和执行器数据。 有关 WADI 数据集的更多详细信息,请参阅 WADI 网站 5。
4.2 Cyber-Attacks(网络攻击)
攻击者的目标是操纵工厂的正常运行。 假设攻击者可以远程访问 SWaT 和 WADI 的 SCADA 系统,并了解系统如何工作的一般知识。 已经在 SWaT 和 WADI 系统上进行了各种实验,以研究网络攻击和相应的系统响应。 总共有 36 次攻击和 15 次攻击分别插入到 SWaT 和 WADI [25,28]。 为了说明,让我们解释每个系统的一个示例性攻击。
– SWaT
一个攻击目标是将 SWaT 的性能从标称水平(例如,5 加仑/分钟)降低到较低的值。 这种攻击可以通过破坏传感器 LIT401 来发起,该传感器测量 P4 中反渗透 (RO) 进料罐的水位。 通过攻击 LIT401,攻击者将 RO 进水罐的水位从 800 毫米降低到 200 毫米,这将导致 PLC-4 停止泵 P401,减少泵入 P5 的水。 最后,攻击传感器 LIT401 的负面影响反映在 RO 单元的输出水流量上(P5 中 FIT501 测量的值)。 根据系统规格,该流速必须保持在大约 1.2 厘米/小时,这导致处理水接近 5 加仑/分钟。 因此,在观察期间减少了处理水的量。
–WADI
一个攻击目标是篡改 P1 中水位传感器的读数。 攻击者将传感器读数从油箱容量的 76% 更改为 10%,这表示“低状态”。 因此,PLC-1(P1 的控制器)发出命令打开进水泵,从 WADI 回水、SWaT 输出或 PUB 入口吸入更多的水。 同时,由于原水箱出现虚假的低水位状态,P1至P2的供水被切断,而P2继续向消费者水箱供水。 因此,P2 中水箱的水位下降。 一旦高架水箱 (P2) 中的水位达到低水位,消费者水箱 (P2) 的供水就会被切断。 因此,通过将P1中水位传感器的读数篡改到低位,P1中的水箱就会溢出,而P2中没有水流。
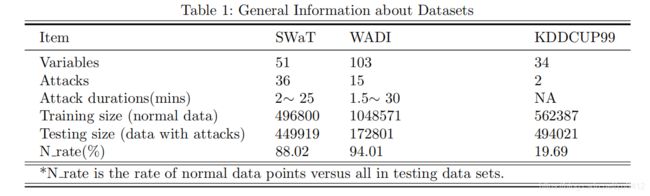
4.3 SWaT 和 WADI 数据集
SWaT/WADI 数据收集过程持续了 11/16 天,系统每天 24 小时运行。 在最后的 4/2 天内,在测试台上执行了各种网络攻击,目的不同,持续时间不同(从几分钟到一个小时)。 在发起另一次攻击或连续发起攻击之前,允许系统达到其正常运行状态。 关于这两个数据集的一些一般信息总结在表 1 中。 为了更好地理解检测任务的复杂性,值得注意的是,这两个数据集及其相关的正常条件和攻击具有以下特征:
- 由于场景不同,不同的攻击可能会持续不同的持续时间。 有些攻击甚至没有立即生效。 系统稳定持续时间也因攻击而异。 更简单的攻击,例如那些旨在改变流速的攻击,需要更少的时间来稳定系统,而对系统动态造成更大影响的攻击将需要更多的时间来稳定。
- 对一个传感器/执行器的攻击可能会影响其他传感器/执行器或整个系统的性能(这一点可以从第 4.2 节的两个示例中看出),通常是在一定的时间延迟之后。
- 此外,类似类型的传感器/执行器倾向于以类似的方式响应攻击。 例如,对 LIT101 传感器(SWaT 的 P1 中的水位传感器)的攻击导致 LIT101 和 LIT301(SWaT 的 P3 中的另一个水位传感器)出现明显异常尖峰,但会影响其他传感器和执行器(如 流量传感器和功率计)相对较小。
上述观察表明,在异常检测系统的建模中采用多变量方法很重要,因为不同子过程的整体性能变化可以共同帮助更好地识别攻击。 换句话说,传感器和执行器之间的潜在相关性可能有助于检测由攻击引起的系统行为异常。
5 实验
5.1 数据准备和系统架构
在 SWaT 数据集中,51 个变量(传感器读数和执行器状态)被测量了 11 天。 在原始数据中,在正常工作条件下(前 7 天收集的数据)收集了 496, 800 个样本,随后在系统中插入各种网络攻击时收集了 449, 919 个样本。 同样,对于 WADI 数据集,前 14 天在正常工作条件下收集了 103 个变量的 789371 个样本,在最后 2 天向系统插入各种网络攻击时收集了 172801 个样本。 对于这两个数据集,我们从训练数据(正常数据)中删除了前 21、600 个样本,因为根据 [26] 首次打开系统时需要 5-6 小时才能达到稳定状态。
在异常检测过程中,我们通过跨越原始流的滑动窗口将原始的长序列细分为更小的时间序列。 由于确定子序列表示的最佳窗口长度是时间序列研究中的一个重要课题,我们尝试了一组不同的窗口大小来捕捉不同分辨率下的系统状态,即 s w = 30 × i , i = 1 , 2 , . . . , 10 s_w = 30 × i, i = 1, 2, ..., 10 sw=30×i,i=1,2,...,10. 为了捕捉 SWaT 数据的相关动态,该窗口应用于正常数据集和测试数据集,移位长度 s s = 10 s_s=10 ss=10。
在本研究中,我们使用深度为 3 的 LSTM 网络和 100 个隐藏(内部)单元作为生成器。 用于鉴别器的 LSTM 网络相对简单,有 100 个隐藏单元,深度为 1。 受到 [7] 中关于潜在空间维度的讨论的启发,我们还尝试了不同的维度,发现更高的潜在空间维度通常会生成更好的样本,尤其是在生成多变量时序列。 在本研究中,我们将潜在空间的维度设置为 15。
5.2 评价指标
我们使用标准指标,即 Precision (Pre)、Recall (Rec) 和 F 1 分数来评估 MAD-GAN 的异常检测性能:

其中 TP 是正确检测到的异常(真阳性: A t = 1 A_t = 1 At=1 而真实标签 L t = 1 L_t = 1 Lt=1),FP 是错误检测的异常(假阳性: A t = 1 A_t = 1 At=1 而真实标签 L t = 0 L_t = 0 Lt=0),TN 是正确分配的正常( 真负例: A t A_t At = 0,而真实标签 L t = 0 L_t = 0 Lt=0),FN 是错误分配的法线(假负例: A t = 0 A_t = 0 At=0 而真实标签 L t = 1 L_t = 1 Lt=1)。
鉴于我们在这项工作中的应用是检测入侵(网络攻击),即使系统需要容忍一些误报,检测所有攻击也很重要。 因此,重点是正确检测实际阳性,而假阳性并不那么重要,只要它们不过量即可。 因此,我们使用召回率作为衡量本研究异常检测性能的主要指标。
5.3 结果
我们评估了 MAD-GAN 在上述两个数据集 SWaT 和 WADI 上的异常检测性能。 如前所述,子序列被输入到 MAD-GAN 模型中。 请注意,为了减少计算负载,我们通过 PCA 减少原始维度,根据 PC 方差率选择 PC 维度。 为了比较异常检测性能,我们还在数据集上应用了 PCA、K-最近邻 (KNN)、特征装袋 (FB) 和自动编码器 (AE),这些都是流行的无监督异常检测方法。 为了与基于 GA 的方法进行比较,我们将 MAD-GAN 与 [12] 的基于高效 GAN(EGAN)的方法进行了比较,后者的鉴别器和生成器是作为全连接神经网络实现的。
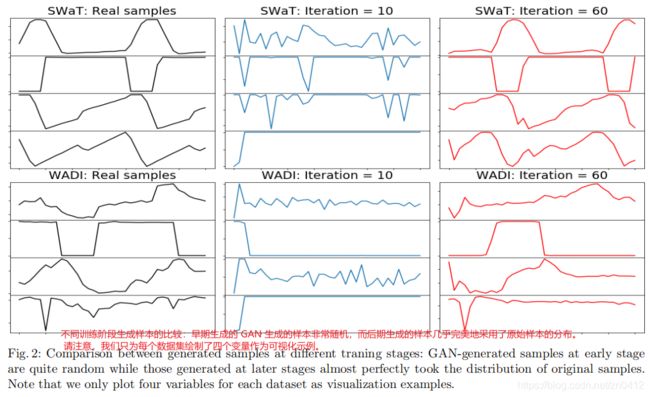
5.3.1 多元生成
首先,我们将 MAD-GAN 生成的多元数据样本与来自 CPS 的实际样本进行可视化。 从图 2 中可以看出,我们的 GAN 生成的样本与早期学习阶段(迭代 = 10)的训练数据明显不同。 然而,经过足够次数的迭代后,生成器能够为系统的各种传感器和执行器输出真实的多变量样本。 请注意,在此可视化示例中,没有将 PCA 投影应用于训练样本(真实样本)。
此外,我们使用最大平均差异 (MMD) [29] 来评估 GAN 模型是否已经学习了训练数据的分布。 MMD 是矩匹配网络的训练目标之一 [30,31]。
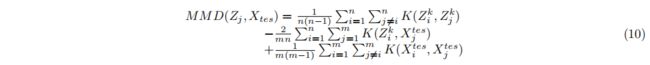
我们绘制了 GAN 训练迭代中的 MMD 值,用于为图 3 中的两个数据集生成多变量样本。我们可以观察到,两个数据集的 MMD 值在 30-50 次迭代后趋于收敛到小值。 我们还比较了单变量样本生成的 MMD 值。 有趣的是,多元样本的早期 MMD 值低于单变量样本,多元样本的 MMD 也比单变量情况收敛得更快。 这表明使用多个数据流有助于 GAN 模型的训练。

5.3.2 异常检测性能
在表 2 中,我们用下划线显示了流行的无监督方法(PCA、KNN、FB 和 AE)的最佳性能,并用粗体显示了整体最佳性能。 如第 5.1 节所述,MAD-GAN 使用多个子序列长度分辨率进行了测试。

从表 2 中,我们观察到以下情况:
- 对于 SWaT 数据集,由于 F 1 平衡精度和召回率,专注于最佳 F 1 选择的结果,MAD-GAN 的性能优于 AE 给出的四种流行方法的最佳性能,其精度和召回率分别为 26.34% 和 11.11%。 事实上,MAD-GAN 在这里实现了接近 100% 的准确率和召回率,为 SWaT 正确检测了所有匿名点而没有误报。
- 对于 WADI 数据集,同样关注最佳 F 1 选择的结果,MAD-GAN 的召回率略低于 AE(低 3.02%)。 然而,对于最好的召回情况,基于召回值,MAD-GAN 的表现比其他人高 65.64 94.36%。 尽管 MAD-GAN 的精度看起来很差,但它可以实现接近 100% 的召回值。 这在网络攻击设置中是可以接受的,因为检测所有入侵的误报成本是可以容忍的(如第 5.2 节所述)。 相比之下,没有一种流行的检测方法可以达到令人满意的召回率。
- 在两个数据集之间,MAD-GAN 对于 SWaT 的表现明显更好。 如表 1 的“N rate”所示,WADI 数据集比 SWaT 更不平衡(即更多的实际负数),这导致更多的误报正数。 此外,我们还注意到,如表 1 所示,WADI 数据集具有比 SWaT 更大的特征维度(WADI 有 103 个变量,而 SWaT 只有 51 个变量。)。
- 在这里,我们还将 MAD-GAN 应用于更平衡的数据集 KDDCUP99 数据集。 在这个数据集上,MAD GAN 可以达到 0.90 F 1 分数,精度大于 85%,召回率大于 94%。 尽管 KDDCUP99 数据集(由 [12] 报告)上的 EGAN 结果比 MAD-GAN 更好(但并非绝对好),但 MAD-GAN 在 SWaT 和 WADI 数据集(不平衡数据集)上的表现都优于 EGAN。 这是因为 MAD-GAN 中使用的 LSTM-RNN 能够比 EGAN 中使用的 CNN 更好地学习复杂的时间序列。 事实上,看看 EGAN 与其他非 GAN 方法的相对性能,我们可以看到,如果我们不对时间相关性进行适当建模,基于 GAN 的异常检测无法与其他传统方法竞争。
总体而言,MAD-GAN 始终优于流行的无监督检测方法。 唯一的缺点是LSTM-RNN需要更多的时间来处理更长的子序列(具体来说,当子序列长度sw大于200时,模型会变慢)。 探索使用其他神经网络来合并时间相关性并考虑未来工作的子序列长度选择是值得的。
5.3.3 降维
如前所述,为了最小化 LSTM-RNN 的计算负载,我们使用 PCA 将原始数据投影到低维主空间,而不是直接将高维数据馈送到 MAD-GAN 模型。 我们在下面的图 4 中绘制了两个数据集的前 10 个主成分 (PC) 的方差率。

该图显示,一台主 PC 解释了 SWaT (WADI) 数据超过 50% (30%) 的方差。 此外,第 5 个(第 8 个)之后的 PC 对整体方差的贡献很小(接近 0)。 因此,我们将 SWaT (WADI) 数据投影到前 5 (8) 个,然后应用 MAD-GAN 检测投影数据的异常。
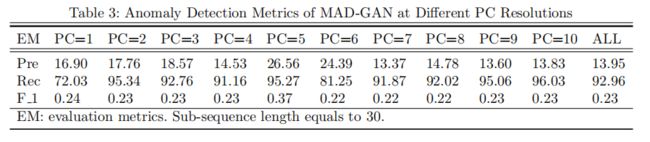
虽然通过降维(减少超过 1/3 的整体训练测试时间)大大减少了计算负载,但可能会丢失信息,这可能会影响真实时间序列数据的生成。 为了表明移除不太重要的变量不会影响异常检测性能,在表 3 中,我们列出了 MAD-GAN 在不同 PC 分辨率(从 PC=1 到 PC=10)以及所有 子序列长度 sw = 30 的 SWaT 数据集的原始变量空间。
从表 3 中,我们观察到以下情况:
- 尽管第一个主成分贡献了 SWaT 数据集方差的 50% 以上(如图 4 所示),但只有这个成分的 MAD-GAN 性能并不令人满意(召回率小于 75%)。 通过添加第二个主成分(前两个主成分共同解释了 SWaT 80% 以上的方差),MAD-GAN 的性能得到了很大的提升,性能(主要通过召回值来评估)普遍收敛在较高的水平 通过添加更多可变维度来提高水平(大于 90%)。
- 通过使用前五个主成分(解释了超过 99.5% 的方差),我们可以实现高于 95% 的召回率。 虽然它比 PC=2,10 报告的召回率差,但 PC=5 获得的精度高于其他人。 这表明合适的特征子集/子组合选择对于减少误报很重要。
- 有趣的是,不同主空间下的 F 1 分数都处于相似的低水平(约 0.22 0.24)。 这是由于精度低造成的,因为 MAD-GAN 报告了不平衡 SWaT 数据集的大量误报。 我们将在下一小节中更多地讨论精度问题。
5.3.4 后续解析
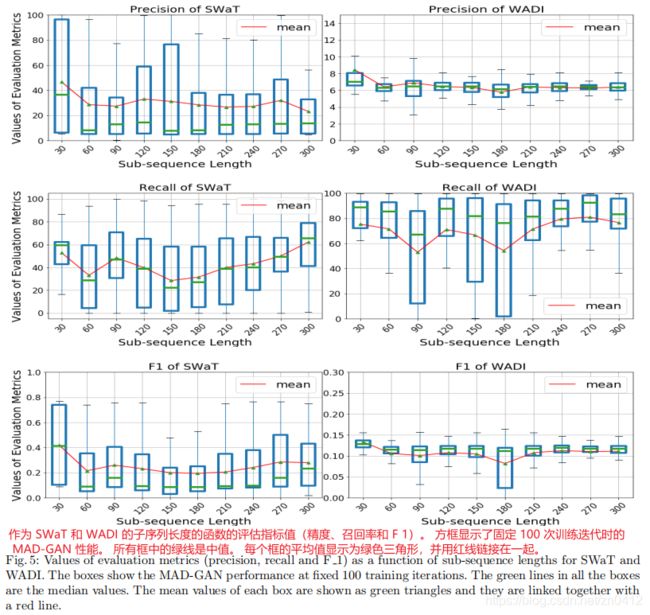
选择合适的子序列分辨率(即子序列长度)对于 RNN 和时间序列相关研究至关重要。 在这项工作中,我们通过尝试一系列不同的子序列长度(即窗口大小)sw = 30 × i, i = 1, 2, …, 10 来凭经验确定最佳子序列分辨率。 对于每个子序列长度 ,GAN 模型递归训练 100 次迭代(即 epochs)。 我们在图 5 中描绘了在不同子序列长度上的每次训练迭代中 MAD-GAN 的召回率和 F 1 值的箱线图。
从图 5 我们可以观察到以下差异:
- SWat 数据集:一般来说,当使用的子序列长度仅为 3 时,MAD-GAN 使用 SWaT 数据集获得更好的度量值(精度、召回率和 F 1)。使用子序列长度 300 时的精度值明显低于使用子序列长度的精度值 较小的子序列长度,而召回值优于 SWaT 数据集不同子序列长度的平均水平。 这表明 SWaT 数据集的子序列长度越大,误报越多(精度差)。
- WADI 数据集:WADI 数据集的整体 F 1 水平较差(小于 0.2),而平均召回值令人满意。 这与我们在 5.3 节中提到的一致。 较差的 F 1(以及精度)是由针对高度不平衡数据报告的大量误报造成的。 然而,鉴于误报对于入侵检测应用来说是相对可以容忍的,这是可以接受的。
虽然性能(特别是召回率)存在波动,并且在测试的子序列长度范围内没有收敛,但我们可以看到,两个数据集的召回率值大致在相对可接受的范围内(50 100%)波动。 因此,相对较小的子序列长度(例如 s w = 30 s_w = 30 sw=30)可能是 SWaT 和 WADI 等 CPS 数据集的安全选择,其中每秒记录一次数据,并且系统具有相对快速的响应 6 ^6 6。 这种选择小的子序列长度可以节省大量时间,同时可以保证性能(如第 5.3.2 节所述,使用超过 200 个子序列的 GAN 模型训练测试需要更多时间)。 对我们来说,研究和开发一种有原则的方法来确定使用 GAN 进行时间序列分析的最佳子序列分辨率,将是一项有价值的进一步工作。
5.3.5 跨多个迭代时期的稳定性
如上所述,MAD-GAN 的稳定性是另一个需要进一步探索的有趣问题。 为了观察训练时期的稳定性,我们将召回值绘制为图 6 中子序列长度 s w = 180 s_w = 180 sw=180 的 SWaT 和 WADI 数据集的迭代时期的函数。 请注意,显示了 100 次迭代的性能,因为我们已将本工作中的实验的训练 epoch 数固定为 100。
从图中,我们可以观察到两个数据集的迭代时期之间的性能(召回值)存在很大差异。 仔细观察可以看出,在最初的几个 epoch 中,性能得到了快速提升,然后开始在相对较高的水平(大于 60%)振荡。 我们在测试 EGAN 时也观察到了类似的波动(它的性能也没有通过增加更多的训练迭代来提高)。 虽然这可能表明少量的训练时期就足以让 MAD-GAN 快速获得令人满意的结果,但随后的振荡表明基于 GAN 的异常检测方法的不稳定性。 作为进一步的工作,值得考虑用于异常检测的 GAN 训练生成器和鉴别器的稳定性。
6 结论
当今的网络物理系统配有联网的传感器和执行器,可生成大量数据流,可用于监控系统行为以检测异常情况,例如由网络攻击引起的异常情况。 在本文中,我们探讨了使用 GAN 对 CPS 生成的时间序列数据进行多变量异常检测。 我们提出了一种新颖的 MAD-GAN(带 GAN 的多元异常检测)框架来在多元时间序列数据上训练 LSTM-RNN,然后利用鉴别器和生成器使用新颖的鉴别和重建异常分数(DR- 分数)。 我们在来自安全水处理试验台 (SWaT) 和配水系统 (WADI) 的两个复杂网络攻击 CPS 数据集上测试了 MAD-GAN,并显示出优于现有无监督检测方法的性能,包括基于 GAN 的方法。
鉴于这是使用 GAN 对时间序列数据进行多变量异常检测的早期尝试,还有一些有趣的问题有待进一步调查。 例如,我们已经注意到确定最佳子序列长度的问题以及 GAN 方法的潜在模型不稳定性。 对于未来的工作,我们计划进一步研究多元异常检测的特征选择,并研究在理论保证下选择潜在维度和 PC 维度的原则方法。 我们也希望对检测模型的稳定性进行详细研究。 在应用方面,我们计划探索将 MAD-GAN 用于其他异常检测应用,例如智能建筑和机械的预测性维护和故障诊断。
