论文笔记： 对抗样本 CVPR2021 Enhance Transferability of Adversarial Attacks through Variance Tuning

论文作者： Xiaosen Wang    Kun He
作者单位： School of Computer Science and Technology, Huazhong University of Science and Technology
作者邮箱： {xiaosen,brooklet60}@hust.edu.cn
源代码： https://github.com/JHL-HUST/VT.

Abstract 摘要

  作者提出一种方法——varirance tuning,其增强了基于梯度迭代攻击方法，提高了攻击的迁移性。
  效果:基于梯度迭代攻击方法加入variance tuning在输入变换以及多模型的设置下，面对9种防御方法可以达到90.1%的平均攻击成功率，将当下最好攻击效果提高了85.1%。

1. Introduction 引言

1.1 背景

  近年来，对抗样本激起广泛的兴趣，一方面其可以检验模型的脆弱性，另一方面可以提供模型的鲁棒性。
  基于白盒攻击生成的对抗样本展现出很好的有效性，但是迁移性低，尤其是攻击使用了防御机制的模型。为解决此问题，当下研究聚焦于提高对抗样本的迁移性，如优化的梯度计算（Momentum，Nesterov’s accelerated gradient 等），攻击多种模型，采用各种输入变换（random resizing and padding, tranalstion, scale, admix, etc.)。然而，白盒攻击与基于迁移黑盒攻击仍有较大差距。

1.2 引入

  作者提出了一种新颖的方法——variance tuning。相较于已有的基于梯度的方法，该方法使用临近过去数据点的梯度变化来额外调节当下梯度。主要思想是在每次迭代时减少梯度的变化，从而在搜素过程中稳定更新方向并摆脱局部最优解。

2. 相关工作 Related Work

1. 符号定义

符号	含义
x	原始图片
y	图片对应的标签
$J(x,y;\theta )$	分类器的损失函数
$x^{adv}$	对抗样本
||$\cdot$||${}_p$	p-范数距离

2.1 对抗样本攻击

1. 对抗样本攻击包括基于梯度的方法(gradient-based methods)、 基于优化的方法(optimization-based methods)，基于分数的方法(score-based methods)，基于决策的方法(decision-based methods)。
2. 聚焦于攻击迁移性，作者简述了基于迁移攻击的两个分支：

• 基于梯度的攻击(Gradient-based Methods)： 应用高级的梯度计算来提高迁移性。如：
  • Fast Gradient Sign Method (FGSM)
    $x^{adv}=x+ϵ\cdot sign({\nabla }_{x}J(x,y;\theta ))$
  • Iterative Fast Gradient Sign Method (I-FGSM)
    $$\begin{gathered} x_{t+1}^{adv}=x_t^{adv}+\alpha \cdot sign({\nabla }_{x_t^{adv}}J(x_t^{adv},y;\theta )) \\ {x}_0^{adv}=x \end{gathered}$$
  • Momentum Iterative Fast Gradient Sign Method (MI-FGSM)
    $$\begin{gathered} g_{t+1}=\mu {\cdot }_t+\frac{{\nabla }_{x_t^{adv}}J(x_t^{adv},y;\theta )}{||{\nabla }_{x_t^{adv}}J(x_t^{adv},y;\theta )|{|}_1} \\ {x}_{t+1}^{adv}=x_t^{adv}+\alpha \cdot sign(g_{t+1}) \end{gathered}$$
    $where{g}_0=0and\mu isthedecayfactor$
  • Nesterov Iterative Fast Gradient Sign Method (NI-FGSM)
• 输入变换(Input Transformations):
  • Diverse Input Method (DIM) : 随机变化大小和填充输入图片
  • Translation-Invariant Method (TIM) : 输入一组图片来计算梯度。为了减少梯度计算，Dong等人在小范围内移动图像，并通过将未变换图像（untranslated images）的梯度与核矩阵进行卷积来近似计算梯度。
  • Scale-Invariant Method (SIM) : 将一张图片缩放$1/2^i$倍数，从而得到一组图片，并计算其梯度（i为超参数）

2.2 对抗样本防御 Adversarial Defenses

  对抗训练(adversarial training) 是一种防御方法——其将对抗样本放入训练数据，从而提高训练出模型的鲁棒性。然而，该方法的缺点在于往往需要高计算代价，并且难以扩展到大规模数据集和复杂的神经网络。
相关研究:

• Guo等人[9] 在将数据输入到模型前，对于输入进行了一系列的图像变换，用以消除对抗扰动的影响。
• Xie等人[34] 对输入进行了随机调整大小和填充(random resizing and padding R&P) 来缓和对抗扰动的影响。
• Liao等人[17] 提出训练一个高级表示降噪器（ high-level representation denoiser HGD来净化输入图像。
• Xu等人[36] 提出两种特征压缩方法: bit reduction(Bit-Red) 和 spatial smoothing，用以检测对抗样本。
• 特征提取(Feature distillation FD)[20] 是防御对抗样本的一种基于JPEG的防御压缩框架。
• ComDefend[12] 是一种防御对抗样本的端到端的图像压缩模型。
• Cohen等人[5] 采用随机平滑(randomized smoothing RS) 来训练可靠的ImageNet 分类器。
• Nasser 等人设计了一个神经表示净化器(neural representation purifier NRP) 模型 ，该模型基于自动获取监督(automatically derived supervision)来净化对抗样本。
• Lin等人[18]融合了DIM，TIM，SIM等方法——Composite Transformation Method(CTM)，是当下最强的基于迁移(transfer-based)的黑盒攻击方法。

3. 方法论 Methdology

3.1 动机 Motivation

  给定目标分类器$f$和原始图片$x$, 对抗样本攻击寻找对抗样本满足：
$$f(x;\theta )\ne f(x^{adv};\theta )s.t.\parallel x-x^{adv}\parallel <ϵ$$
  对于白盒攻击，将其看做一个优化问题——即在$x$周围寻找一个样本，使之能最大化目标分类器的损失函数:
$$x^{adv}=argma{x}_{\parallel x^{\prime }-x{\parallel }_p<ϵ}J(x^{\prime },y;\theta )$$
  Lin等人[18]将对抗样本生成过程类比为标准神经网络的训练过程，即输入图像$x$作为参数被训练，目标模型最为训练集。由此看，对抗样本的迁移性可以等价于正常训练模型的泛化能力。因而，已有的一些方法聚焦于更好的优化算法（如MI-FGSM, NI-FGSM），或数据增强（整合多种模型进行攻击，或输入变换）。
  作者将基于梯度迭代的对抗攻击算法看作一个随机梯度下降（SGD）的优化过程。作者指出SGD由于随机性致使方差较大，进而导致了慢收敛。对此，已经有多种方差降低技术（variance reduction）如SAG(stochastic average gradient), SDCA(stochastic dual coordinate ascent), SVRG(stochastic variance reduced gradient)，此外， Nesterov’s accelerated gradient 可以加速收敛，提高攻击迁移性。
 
  作者方法variace tuning与SGD with variance reduction methods(SGDVRMS)的不同：

• variance tuning致力于生成高迁移性的对抗样本，而SGAVRMS目的在于加速收敛
• variance tuning方法的gradient variance来自于输入x的近邻（neighborhood)，而SGDVRMS使用的是训练集中的variance
• variance tuning 更具泛化性，能用于提高MI-FGSM和NI-FGSM的性能。

3.2 Variance Tuning Gradient-based Attacks

  典型的基于梯度迭代的攻击(如I-FGSM) 在每次迭代过程中根据梯度的符号方向搜寻对抗样本，但容易陷入局部最优，或过拟合。MI-FGSM加入了动量，以稳定更新方向，逃离局部最优。NI-FGSM进一步采用了Netserov’s accelerated gradient 来迁移性。
  作者在上面基础上，提出利用之前数据的临近数据的梯度信息来调节当下数据的梯度。

梯度变化(Gradient Variance)的定义：
  给定分类器f，参数$\theta$, 损失函数$J(x,y;\theta )$, x 为图像，${ϵ}^{\prime }$为近邻范围的上限, 则梯度变化可定义为：
$$V_{{ϵ}^{\prime }}^g(x)={\mathbb{E}}_{\parallel x^{\prime }-x{\parallel }_p<{ϵ}^{\prime }}[{\nabla }_{x^{\prime }}J(x^{\prime },y;\theta )]-{\nabla }_{x}J(x,y;\theta )$$
  其中, ${ϵ}^{\prime }=\beta \cdot ϵ$, $\beta$是一个超参数，而$ϵ$是扰动数量级的上限。
  实际过程中，由于输入空间的连续性，上式无法计算。因而，作者通过采样的方式近似得到结果：
$$V(x)=\frac{1}{N}\sum _{i=1}^N{\nabla }_{x^i}J(x^i,y,\theta )-{\nabla }_{x}J(x,y;\theta )(7)$$
  上式中，V(x)为$V_{{ϵ}^{\prime }}^g(x)$ 简写，$x^i=x+r_i$, $r_i\sim U[-(\beta \cdot ϵ{)}^d,(\beta \cdot epsilon{)}^d]$。

3.3 各种攻击之前的关系

  使用了variance tuning方法的攻击，在方法名前面加入了"V",如VMI-FGSM。

• 当$\beta =0$时，VMI-FGSM和VNI-FGSM就退化为了MI-FGSM和NI-FGSM。
• 如果衰减因子$\mu =0$,那么MI-FGSM和NI-FGSM就退化为了I-FGSM。
• 如果迭代次数为1，那么I-FGSM就退化为lGSM。

4. 实验

4.1 实验准备

• 数据集：从ILSVRC2012验证集中1000个类别随机挑选1000张图片。
• 模型： Inception-v3 (Inc-v3) , Inception-v4 (Inc-v4), Inception-Resnet-v2 (IncRes-v2), Resnet-v2-101 (Res-101) 以及三个对抗训练的模型：$Inc-v{3}_{ens3}$, $Inc-v{3}_{ens4}$ 和 $IncRes-v{2}_{ens}$。 此外，作者还是用了九种先进的防御模型：HGD, R&P, NIPS-r3, Bit-Red, JPEG, FD, ComDefend, RS, NRP等。
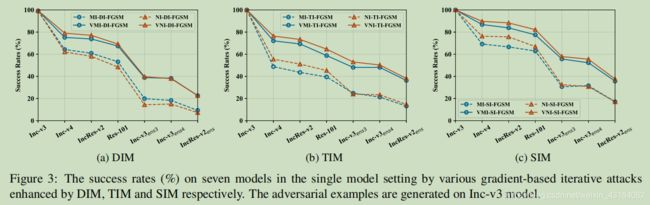
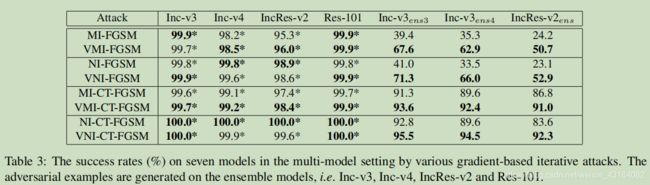
• 基准(Baselines): 作者采用MI-FGSM 和NI-FGSM，此外作者还将这两种方法整合了各种输入转换方法（DIM, TIM, SIM和CTM），表示为VM(N)I-DI-FGSM, VM(N)I-TI-FGSM, VM(N)I-SI-FGSM 和 VM(N)I-CT-FGSM。
• 超参： 最大扰动$ϵ=16$，迭代轮数T=10，则 每次迭代的大小$\alpha =1.6$。 对于MI-FGSM和NI-FGSM，衰减因子$\mu =1.0$。 对于DIM，变换概率设为0.5。对于TIM，采用$7\ast 7$的高斯核。对于SIM，图像张数为5。 对于本方法，$N=20,\beta =1.5$。

4.2 攻击一个模型

4.3 带有输入变换的攻击

4.4 攻击一组模型

4.5 攻击高级防御模型(Attack advanced defense models)

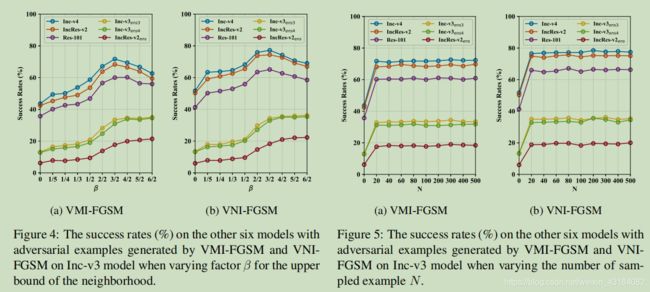
4.6 超参消融实验

  对于近邻范围的上限$\beta$,$\beta =3/2$时攻击正常训练模型，迁移性能达到最高。
  对于近邻范围的采样数量N, N取20时，迁移性获得显著提升。再增大N，其增长缓慢。

5. 总结

  Variance tuning可以显著提高已有攻击方法（如MI-FGSM, NI-FGSM等）的迁移性。它可以应用于任何基于梯度的迭代攻击。