机器学习：绪论及模型评估与选择

引言：

本篇笔记是已周志华老师写的《机器学习》前两章进行概述的，这次笔记仅仅只是带表了我个人的看法，其中有写的不好的地方还希望大家能够指出，以后会多多改正，争取日益进步。

第一章：绪论

1.1基本术语：

以西瓜为例，收集了一些有关西瓜的数据。（色泽=青绿；根蒂=蜷缩；敲声=浊响……）我们把色泽，根蒂，敲声称之为属性，属性的取值例如青绿，蜷缩，浊响称之为属性值。属性张成的空间我们就称为：“属性空间”，“样本空间”或“输入空间”。

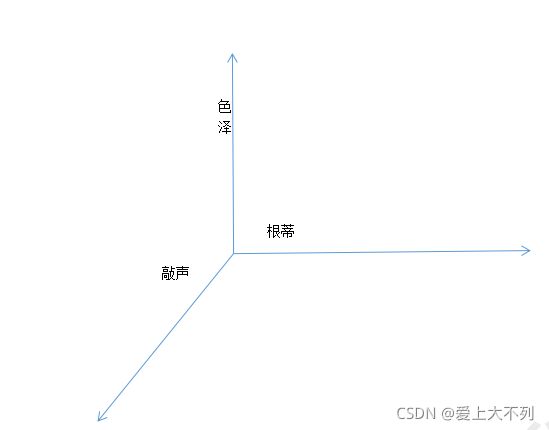
如图，这就是一个属性空间。

一般，另D={X1，X2，X3……，Xm}包含了m个数据集，。每个数据集又能包含d个属性描述，Xi就是d维样本空间中的X的一个向量了，如Xij是X在第i个上的j的属性向量，d就称为样本Xi的维数。

从数据中学得模型过程称为“学习”或者“训练”，这个过程一般需要算法来进行实现。如我们需要一个模型来判断是否是一个好瓜，我们则需要得到训练样本的很多“结果”信息（色泽=“青绿”，根蒂=“蜷缩”，敲声=“浊响”，好瓜！）。称为标记，让机器来进行辨别是否是好瓜。

模型之后，使用模型进行预测的过程称为“测试”（testing),被预测的样本称为“测试样本”。

我们对西瓜进行“聚类”，即将训练集中的西瓜分为若干类，每组称为一个“簇”，每组簇能对应一些潜在的概念划分，如：“浅色瓜”，“深色瓜”。
注意：浅色瓜和深色瓜这些概念我们本来是不知道的，是系统自己归纳出来的

我们根据训练数据是否有标记信息，可以分为两类：“监督学习”和“无监督学习”，分类和回归是前者的代表，聚类则是后者的代表。

我们的目标是使学得的模型能很好的适用于“新样本”，这种能力叫“泛华能力”。即使只有一小块样本空间，但只要有很强的泛华能力，自然也可适应样本空间的特性。

1.2假设空间：

归纳和演绎是科学推理的两大基本手段。“从样例中学习”显然是一个归纳学习的过程。

概念学习最基本的是布尔概念学习，即是与不是，表示为0/1的布尔值的概念目标学习。如：

编号	色泽	根蒂	敲声	好瓜
1	青绿	蜷缩	浊响	是
2	乌黑	蜷缩	浊响	是
3	青绿	硬挺	清脆	否
4	乌黑	蜷缩	沉闷	否

此处要学习的目标是“好瓜”，我们需要判断“色泽”“根蒂”“敲声”这三个因素。来确定他是不是好瓜，也就是说好瓜等价于（色泽=？） ^ (根蒂=？） ^(敲声=？），我们就是通过学习将？的值来进行确定下来。

但是，我们仅仅是“记住”这个是“达媚”的，如果出现了一个未曾见过的，那就宣告寄了。如：色泽=纯黑。

我们把学习的过程中看做事一个在假设空间进行搜索的过程，进行匹配找到正确的假设，这就是学习。假设的表示一旦确定，那么他的规模也就确定了，如，此处我们假设空间由（色泽=？） ^ (根蒂=？） ^(敲声=？）三部分来确定。如果色泽取什么值都合适，我们就将他记做“*”。如：（色泽= *） ^ (根蒂=？） ^(敲声=？）。如果世界上没有好瓜，我们就用∅来表示它。如：西瓜问题的假设空间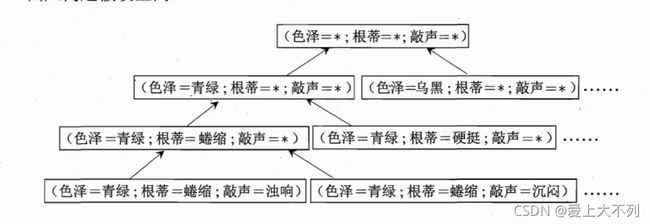

1.3假设空间

当“好瓜”的标准再次上升了，如：（色泽=青绿） ^ (根蒂=蜷缩） ^(敲声=沉闷），如果采用好瓜等价于（色泽= *） ^ (根蒂=蜷缩） ^(敲声= *）我们会把他判断成好瓜，如果采用其他两个方案选择，则为烂瓜。那么该采用哪个模型呢？
接下来让我举个栗子：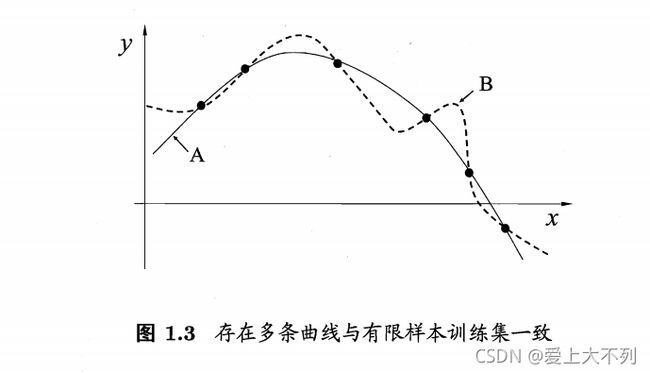
如，A,B都是两个瓜，认为相似的样本应有相似的输出，我们则认为A是比B好的瓜。有没有一般性的原则来引导什么是好瓜呢？自然是有的啊

“奥卡姆剃刀” 原则 ：若有多个假设与观察一致，我们选择最简单的那个

A和B 比较，自然是A简单。

但是，“奥卡姆剃刀”并非唯一可行原则，他自己也是有矛盾的，如：（色泽= *） ^ (根蒂=？） ^(敲声= *） 和 （色泽= ？） ^ (根蒂= *） ^(敲声= *），这两个哪个更简单呢？哎，这就是矛盾了，所以说这个问题并不简单，我们借助其他机制。

如这个算法，显示A和B的期望值是相同的。也就是说A和B一样。即“天下没有免费的午餐”道理。简称NFL定理了。（好吧，说实话，到这我也是一头雾水，看不明白的，雀氏难啊，我想啸啊！！#狗头保命）

第二章：评估模型与选择

2.1经验误差与过拟合：

通常我们把分类错误占样本总数的比例称为”错误率“，如果m个样本中有a个错误，那么错误率 E= a/m，精度 = 1-E.学习器在训练集上的误差称为“训练误差”或者“经验误差”。显然，我们希望误差是不是越小越好呢？但是，非常遗憾，事实总是事与愿违。

我们所希望的，是在新样本上表现的很好的学习器。当我们把学习器训练的太好的时候，它就会把训练器本身的一些特点当做所有潜在样本都具有的一般性质，我们称之为“过拟合”，相反则是“欠拟合”。
如图：

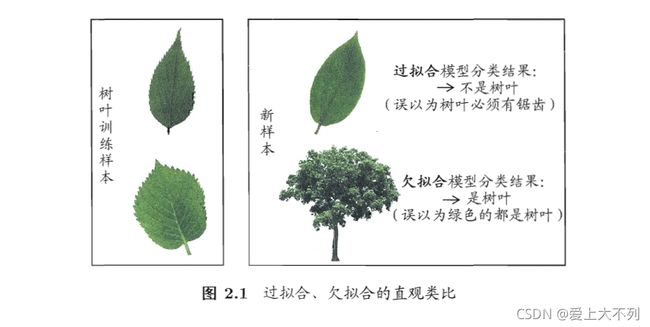
2.2评估方法

通常，我们可通过实验测试来对学习器的泛华误差进行评估并作出选择。为此，我们需要“测试集”来进行评定，此外我们也需要“训练集’进行学习器的训练，要注意的是测试样本尽量不要在训练集中出现。

当我们只有一个包含m个样例的数据集 D={(x1,y1),(x2,y2)……(Xm,Ym)}既要训练，又要测试时，我们究竟该如何是好？以下有几种常见的方法：

2.2.1留出法

留出法是将数据D划分为两个互斥的集合，训练集S与测试集T，即 D = S∪T,S∩T=∅。

假设D 包含1000个样本，S=700，T=300，S训练之后，T出现90个错误，错误率E = 90 / 300 = 30%。精度则为70%。

但是此处有一窘境：若令S包含绝大多数样本，那么T就较少，测试的结果可能不够准确。若T包含大多数样本，则S训练的过少，被评估的模型与D有较大的差距，我们最好的做法是将大约2 / 3 —— 4/5的样本用于训练，其余测试。

2.2.2交叉验证法

“交叉验证法”将数据分为k个大小相似的互斥子集，即D = D1∪D2∪D3……∪Dk，Di∩Dj = ∅。用k个子集作为训练集，余下的作为测试集。
如图：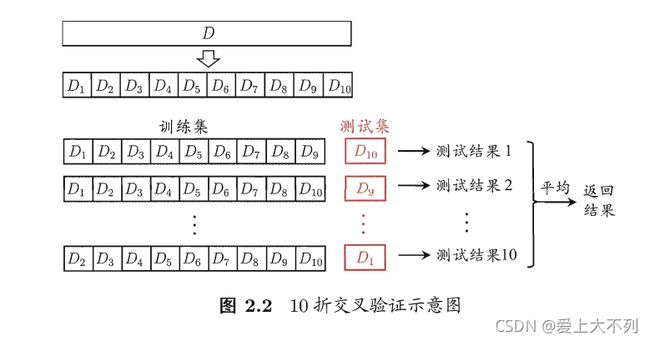

假定数据集D包含m个样本，令k=m，则得到了交叉验证法的特例：留一法。可见，留一法不受随机样本划分的影响，但是留一法的弊端也显而易见了，那就是太花钱了，呜呜呜。如数据包含100w个模型，则需要训练100个w（你缺w吗？水太深，你把握不住，叔来帮你把握 #狗头）。

2.2.3自助法

自助法以自助采样为基础，如D有m个数据，我们采样数据为D‘，随机採一个放入D’中，在将其放入D中。我们重复执行m次。显然D中样本一部分会在D’中出现，另一部分则不会。样本m次采样中不被採到的概率为（1-1/m)^m，取极限得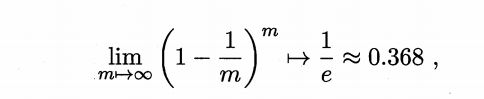
也就是说我们有0.368的数据不会被采到。

自助法适用于数据集较小，数据集较大则使用留出法和交叉验证法。

2.2.4调参与最终模型

大多数算法都有参数需要设定，配置不同，学得的模型性能就会有差异。因此我们需要参数调节，就是：“调参”。

如在[0,0.2]的过程中已0.05为步长，则实际有5个参数，从5个中选定最终值。此外，我们通常把学得的模型在实际使用中遇到的数据成为“测试数据”，为了区分，模型评估与选择中用于评估测试的数据集常成为“验证集”。

2.3性能度量

对学习器的泛化性能进行评估，不仅要有实验估计方法，也要有衡量泛华模型的评价标准，这就是性能度量。

在预测任务中， D={(x1,y1),(x2,y2)……(Xm,Ym)}其中，Yi是Xi的真实标记。
我们最常用的是均方误差。

此外，对于数据分布D和概率密度函数p，均方误差描述为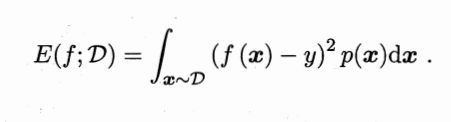
以下为介绍分类任务中常用的性能度量

2.3.1错误率与精度

错误率的定义为：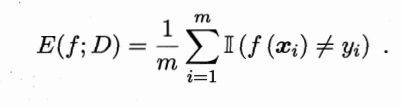
精度则定义为：
对于数据分布D和概率密度函数p，错误率与精度描述为：

2.3.2查准率、查全率与F1

错误率与精度虽常用，但不能满足所有问题。需要其他性能度量。
对二分类问题，可划分为，假正例，真正例，真反例，假反例。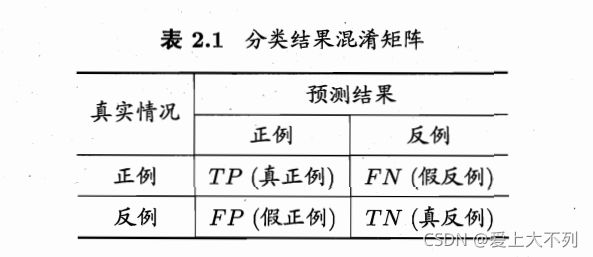
查准率P与查全率R的定义为：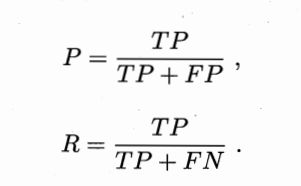
查准率与查全率一般是矛盾变量，当前者高时，后者自然低。

很多情况下，我们会已查准率和查全率进行做曲线，称P-R曲线。
如图：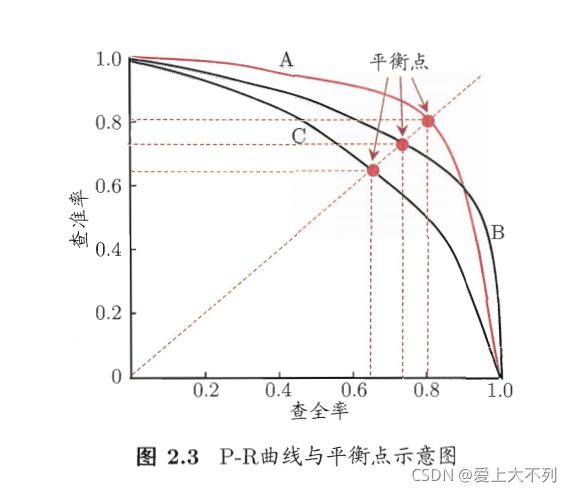
平衡点是人们综合考虑查准率，查全率的一个性能度量，简称BEP。
但是BEP还是达咩的，一般都用F1度量。（F1=(B+R)/2)