ResNet 论文阅读笔记
ResNet 论文阅读笔记
#机器学习/深度学习
文章介绍
论文地址:https://arxiv.org/pdf/1512.03385.pdf
原文题目:Deep Residual Learning for Image Recognition
作者: Kaiming He 团队 (微软亚洲研究院)
该文是2016年CVPR 最佳论文,拿下来当年 ImageNet 等数据集以及各项比赛第一名。提出的 ResNet 是基于残差学习,让神经网络训练起来更加容易。直观上来说,神经网络可以越做越深、准确度也可以越来越高。 ResNet 也揭开了卷积神经网络的新篇章。
研究现状
随着之前 12年 AlexNet 的提出,在 imageNet 上取得了惊人表现,卷积神经网络在计算机视觉领域变得一发不可收拾。而在该 ResNet 发布之前,普遍的、主流的卷积神经网络主要是越做越深,但实际效果上,并不是卷积层的越深越好,(这与 AlexNet 作者提出越深越好不符合,受限于当时的GPU发展,AlexNet 只提出了 五层的卷积层、三层的全连接层)。
作者指出当前神经网络现状,更深的神经网络非常难于训练。
提出了一种基于残差学习的框架,简化了对神经网络的训练,使得神经网络可以比之前的深得多。
重新定义了一种残差学习层,通过拟合残差而不是去拟合期望的潜在映射。
卷积神经网络似乎并不是越深越好 (Is learning better networks as easy as stacking more layers?)
当你的网络特别深的时候:网络的梯度很容易要么消失、要么爆炸。导致训练失败,无法得到一个有效的模型。
解决它的一个办法是,在初始化的时候,权重要初始化合适一点,不能太大不能太小( normalized initial-
ization)。或者在中间加入 normalization layers。
而采取上面两种举措来使得模型可以在训练下收敛后,暴露了一个新的问题:
“with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly.”
作者提出,这并不是由于模型复杂导致的过拟合产生的。如下:
ResNet 论文中展示出下图说明:
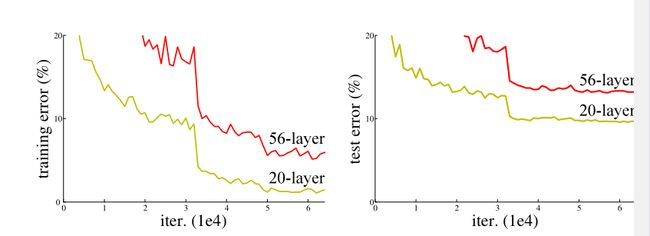
从上图看出,在CIFAR-10 的数据集上,20层和56层的神经网络相比,56层的神经网络表现还比不上20层的神经网络。且56层的神经网络不论是在训练集上还是在验证集上,其表现都是不如20层的,即56层的效果差并不因为模型太复杂导致的过拟合现象。(即似乎、层数越深、网络反而退化了)。
如何避免且构造更深的网络
作者提出一个解决方案。对于一个较浅的神经网络模型上进行改造,在这个常规的较浅的模型上添加新的层,而新的层是原模型的 identity mapping,即恒等映射。即输入和输出是相同,可以看作新加的层是简单的恒等映射,输入什么输出什么。
那么按照这种假设,新的模型与原较浅模型相比较,理论上新模型至少不应该比原较浅模型差。因为在恒等映射下,新加的层可以让它的贡献为0,这样新模型其实和原模型是一样的。这个假设即 ResNet 的出发点。
但在实践表明,增加网络的层数之后,训练误差实际上不降反升(如上图)。
提出 deep residual learning framework
为了解决以上假设的问题(跟深的层并没有得到更好的结果),作者提出了一种深度残差学习框架,而不是直接拟合出一个期望的潜在映射。
常规的神经网络可以看成卷积层的堆叠,也可称为卷积栈,在文中作者称其为 plain network,也就是简单堆叠层的网络。 输入的数据经过每个卷积层都会发生变化,产生新的特征图,可以看作数据在输入和输出间发生了映射。 ResNet 思想即与其让卷积栈直接训练拟合 这种潜在的期望的映射,不如让他去拟合 residual mapping,而这里的 残差映射(residual mapping) 与 潜在映射(underlying mapping)是有关联的。如下图(图片来着作者何凯明在做现在演讲报告时的PPT,从视频中截图)
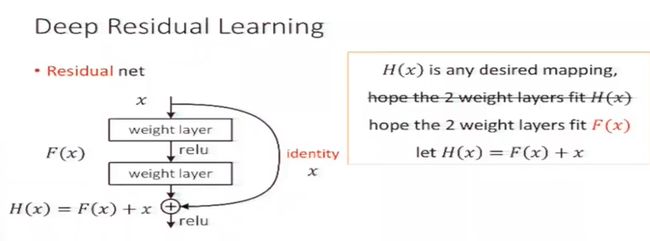
若设原本两层神经网络拟合到的输出为 H ( x ) H(x) H(x) ,也为我们传统神经网络要拟合的输出,我们以前不适用残差网络即直接拟合得到一个期望的映射 H ( s ) H(s) H(s)
现在将两层网络的直接输出表示改为 F ( x ) F(x) F(x),而残差网络拟合的为 F ( x ) + x = H ( x ) F(x) + x = H(x) F(x)+x=H(x),即不再是单纯的神经网络输出,而是再加上了原本的输入 x x x。
从图中看出,最后这一部分残差网络的输出 H ( x ) H(x) H(x) 变为了 F ( x ) + x F(x) + x F(x)+x,而按照上面作者提出的假设,要让其变为恒等映射即
x = H ( x ) = F ( x ) + x x = H(x) = F(x) +x x=H(x)=F(x)+x
只需要将F(x) 的参数全设为 0 ,即等式成立,残差网络完成了恒等映射。 F ( x ) = y − x F(x) = y -x F(x)=y−x 也叫做残差项,要让 x − > y x -> y x−>y 的映射接近恒等映射(identity mapping),即通过学习残差项 F ( x ) F(x) F(x) 到零比直接在神经网络层的堆叠上更加容易。
We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.
原文:我们假设优化残差映射比优化原始的未参考映射更容易。极端情况下,如果恒等映射是最优的,将残差优化到零比用一堆非线性层来拟合一个恒等映射要容易得多。
上图这种结构也叫残差块(residual block)。 输入x 通过跨层链接,更快的前向传播,或者后向传播梯度。这种 x x x 跨层链接称为 “shortcut connections” ,翻译过来也为 捷径连接。在这残差网络结构(残差快)中,shortcut connections执行得即恒等映射的作用,直接将这个 x x x 的恒等输出加在了堆叠层的输出上。(如上图)
捷径连接不会添加额外的参数或者计算复杂度,所以不会提高训练难度,整个模型仍然可以通过随机梯度下降SGD和反向传播来完成端到端的训练。
这种深度残差学习网络,在各项数据集上都有很好的表现,且大大超过第二名。作者通过这些数据集证明:
- 哪怕他们很深的残差网络模型,都很容易去优化、训练,但对应的简单的层堆叠网络却展现出,随着深度越高、训练误差验证误差也在增加。(这个在第一部分即提到)
- 作者提出的深度残差网络,可以从越来越深的网络模型中得到越来越高的准确度收益。
Deep Residual Learning
Residual Learning
这部分详细说明了残差学习,以及为什么采用它。
作者假设:加入多层的非线性层可以渐进的逼近一个复杂函数 ,那么等同于它可以渐进的逼近残差函数 H ( x ) − x H(x) - x H(x)−x。(假设输入和输出维度相同)
So rather than expect stacked layers to approximate H(x), we explicitly let these layers approximate a residual function F(x) :=H(x)−x.Although both forms should be able to asymptotically approximate the desired functions (as hypothesized), the ease of learning might be different.
因此,与其期望堆叠层去拟合(渐进逼近)得到 h (x) ,我们不如让这些层接近残差函数 f ( x ) : = h ( x ) − x f (x) : = h (x)-x f(x):=h(x)−x,原函数因此变成 f ( x ) + x f(x)+x f(x)+x。虽然两种形式应该都可以渐近地接近期望的函数(如同上面的假设),但两者的学习难度程度是不同的。(多层网络为什么难以拟合恒等映射问题,涉及到了信号与系统的知识)
这里这个假设仍然是一个悬而未决的问题。
这个重建或者说深度残差网络的提出的动机即是上面第二节的违反直接的现象:
- 如果新增加的层可以被构造为恒等映射,一个更深模型的训练误差不应该比原本的浅的模型更大。(即表明新增加的多层非线性层难以逼近恒等映射)
构建残差学习网络后,如果恒等映射是最优的,那么学习器会简单的使多层非线性层的权值趋近于 0 来使整个非线性层逼近恒等映射。
注意,上面阐述的都是在恒等映射为最优的情况下,但在大多数情况下,恒等映射并不是一个最优的情况,(即便为恒等映射,也只是让加深后的模型于原本的浅层模型等效一样而已)。我们需要得到一个最优,而这重构的残差学习会帮助预测问题。
残差结构为什么有效?:(这部分内容参考自:ResNet论文笔记及代码剖析 - 知乎)
- 自适应深度: 网络退化问题就体现了多层网络难以拟合恒等映射这种情况,也就是说 H ( x ) H(x) H(x) 难以拟合 x x x 。但使用了残差结构之后,拟合恒等映射变得很容易,直接把网络参数全学习到为0,只留下那个恒等映射的跨层连接即可。于是当网络不需要这么深时,中间的恒等映射就可以多一点,反之就可以少一点。体现了自适应深度的特点。
- 差分放大:假设最优的映射 H ( x ) H(x) H(x) 更接近与恒等映射,那么网络更容易发现除恒等映射之外的微小波动。
- 缓解梯度消失 :对于一个残差块求对输入 x x x 求导即可发现,对于跨层连接的 x x x ,总梯度在 F ( x ) F(x) F(x) 对 x x x 的导数的基础上还要加1。有效缓解了在很深的网络模型中,由于模型深度导致的梯度消失。
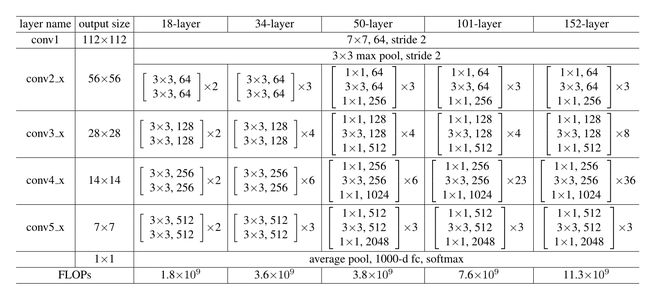
ResNet 网络结构
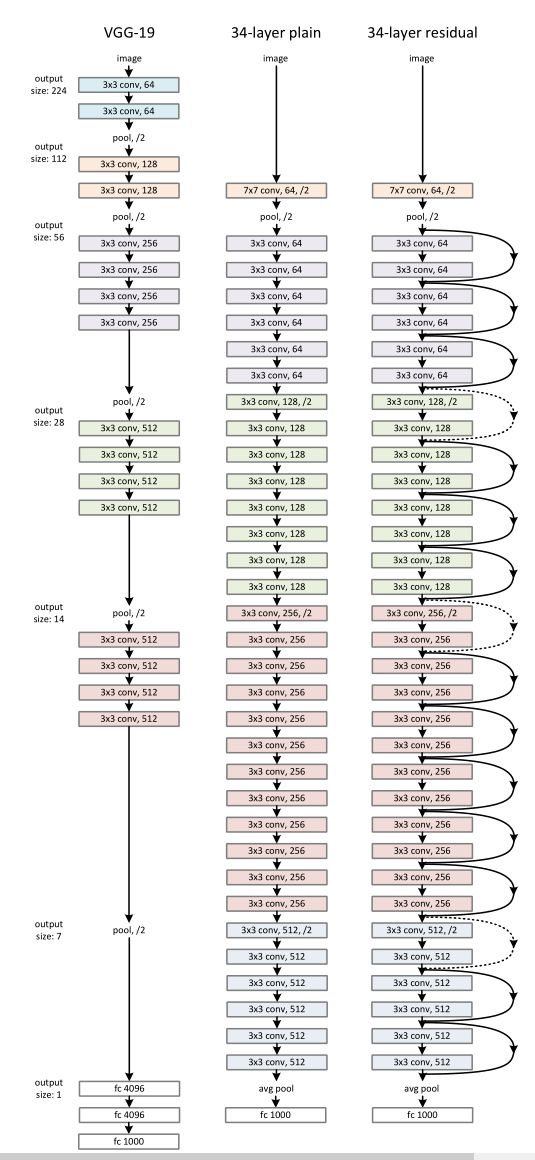
上图为作者为 ImageNet 设计的网络模型,从左到右分别为 VGG-19、作者自己仿照 VGG-19设计的 34层堆叠层、ResNet-34。
每一层都给出了卷积核的大小,卷积核的数目,输出的大小。图中不同的颜色代表不同的输出尺寸、卷积核的数目。
作者提到,每经过一次下采样(池化)将输入尺寸、维度减半后,都将卷积核的数目翻倍,保证每层相同的时间复杂度。(图中虚线的 shortcut connections 代表对 x x x 进行一次降维,以匹配和 f ( x ) f(x) f(x) 相加)
最后倒数第二层采用的全局平均池化(global average pooling,对每个特征图求平均值),最后再接上一个1000个神经元的全连接层和一个Softmax。(因为这里的 ImageNet 输出的1000个类别)。
其他层数的ResNet
FLOPs代表计算复杂度。
34层的构造如下,其他层同理:
首先一共有(3+4+6+3)= 16个残差块,每个残差块有2两层卷积层,一共16x2 = 32层卷积层,加上一层输入卷积层和输出全连接层,一共32+2=34层。
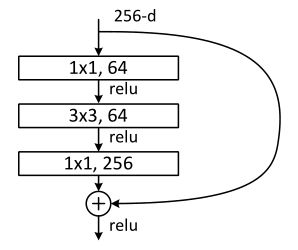
对于50层以上的 ResNet ,采用了这种名为 “bottleneck” 的结构(如上图)。比如上图即先用64个尺寸为1x1的卷积核将输入降维为64,最后再经过一个256个尺寸1x1的卷积核升维。注意bottleneck中3 x 3的卷积层只有一个,而不是普通结构的两个
总结:
作者在 ImageNet 验证集上的表现证明了 ResNet 比当时其他网络模型要强很多,且 ResNet 本身深度越高准确率越高。
作者在除了在 ImageNet ,也在 CIFAR-10 数据集上进行了分析和测试,其表现也远远比其他的要强。且由于CIFAR-10数据集较小,作者在CIFAR-10数据集上做到了1000层以上的 ResNet。
基于残差学习的 ResNet,其思想可以让神经网络越做越深,同时更好拟合。深度越深准确度越高,且相比于之前读过的 AlexNet ,作者在 ResNet 上的论述更加充分,令人信服。且 ResNet 没有如同 AlexNet一般采用好几层的全连接层,只采用了一层全连接层作为 softmax 分类,大大降低了计算的复杂度,提高了模型的训练效率。