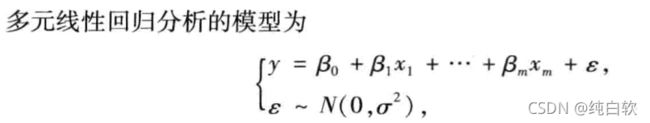Matlab第四天打卡——线性回归
学习Matlab的第四次
目录
一、一元线性回归。
①例题
②分析
③利用Matlab绘图
④进一步拟合
⑤获得回归方程
二、多元线性回归
Ⅰ、模型
Ⅱ、例题
Ⅲ、代码实现
三、参考文档
一、一元线性回归。
一元回归方程比较简单,我们只需要自变量![]() ,因变量
,因变量![]() 的部分数据,经过绘出散点图,就可以进行拟合。
的部分数据,经过绘出散点图,就可以进行拟合。
①例题
②分析
x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];③利用Matlab绘图
clc;
clear;
x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];
for i=1:10
plot(x(i),y(i),'or');
%plot(X,Y) 创建 Y 中数据对 X 中对应值的二维线图。
%o代表以圆圈为图像,r为'red'红色。
hold on
%添加新绘图时保留当前绘图,使所有点一起绘出。
end
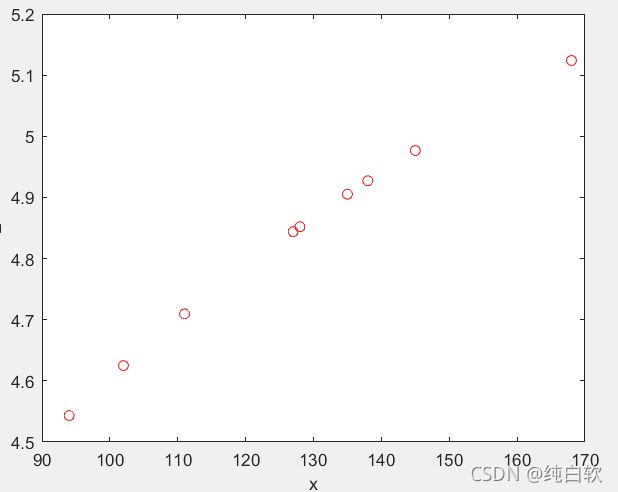
xlabel('x');%x轴元素为x
ylabel('y');%同上
可以得到
此时我们已经可以进行拟合,因为它的点大致处于一条直线附近,但是我们可以发现,x与y似乎是对数关系,所以可以进行进一步的精细。
④进一步拟合
由此经过观察我们可以另作![]() ,对z与x进行绘图。
,对z与x进行绘图。
clc;
clear;
x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];
z=zeros(size(x));
%获得向量x的大小
n=length(x);
%获得向量x的长度
for i=1:n
z(i)=log(x(i));
plot(x(i),z(i),'or');
%plot(X,Y) 创建 Y 中数据对 X 中对应值的二维线图。
%o代表以圆圈为图像,r为'red'红色。
hold on
%添加新绘图时保留当前绘图,使所有点一起绘出。
end
xlabel('x');%x轴元素为x
ylabel('z');%同上可以得到
现在可以看出它的拟合效果更加直观。
⑤获得回归方程
根据第④步得到的图像,我们可以近似看为一条![]() 的直线。
的直线。
因此
clc;
clear;
x=[168 145 128 138 145 135 127 111 102 94];
y=[661 631 610 588 583 575 567 502 446 379];
z=zeros(size(x));
%获得向量x的大小
n=length(x);
%获得向量x的长度
for i=1:n
z(i)=log(x(i));
end
%p = polyfit(x,y,n)返回次数为 n 的多项式 p(x) 的系数
p=polyfit(x,z,1)可以得到
因此![]() 所以
所以![]()
二、多元线性回归
Ⅰ、模型
基础为最小二乘法
在Matlab中可以用到函数
[b,bint,r,rint,stats]=regress(y,x,alpha)
①alpha为显著性水平,默认值为0.05
②b为多元线性回归的系数估计值,以数值向量形式返回
③bint系数估计值的置信边界下限和置信边界上限,以数值矩阵形式返回
④r为残差,以数值向量形式返回
⑤rint为用于诊断离群值的区间,以数值矩阵形式返回
⑥stats为模型统计量,以数值向量形式返回
Ⅱ、例题
Ⅲ、代码实现
clc;
clear;
x1=[1.376 1.375 1.387 1.401 1.412 1.428 1.445 1.477];
x2=[0.450 0.475 0.485 0.5 0.535 0.545 0.55 0.575];
x3=[2.17 2.554 2.676 2.713 2.823 3.088 3.122 3.262];
x4=[0.8922 1.161 0.5346 0.9589 1.0239 1.0499 1.1065 1.1387];
y=[5.19 5.3 5.6 5.82 6 6.06 6.45 6.95];
%数据输入
y=y';
%变为列向量
x=[ones(size(x1')),x1',x2',x3',x4'];
%构造成矩阵
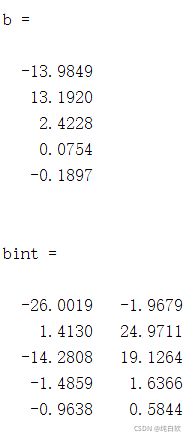
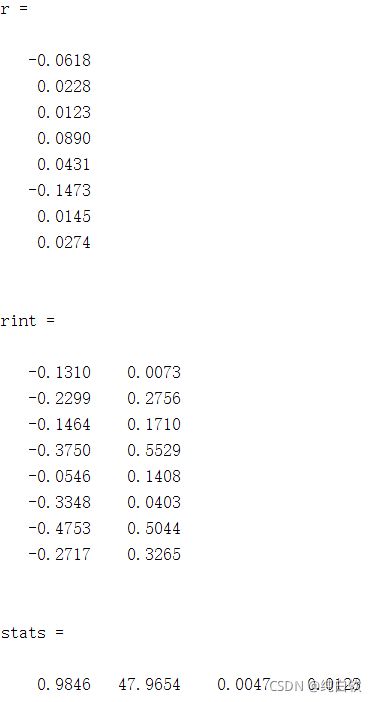
[b,bint,r,rint,stats]=regress(y,x)
因此由b的返回值可得 ![]()
三、参考文档
来自Matlab自带文档
%[b,bint,r,rint,stats]=regress(y,x)
https://ww2.mathworks.cn/help/stats/regress.html?s_tid=doc_ta
%plot
https://ww2.mathworks.cn/help/matlab/ref/plot.html?s_tid=srchtitle_plot_1
%ployfit
https://ww2.mathworks.cn/help/matlab/ref/polyfit.html?searchHighlight=ployfit&s_tid=srchtitle_ployfit_1
%hold on
https://ww2.mathworks.cn/help/matlab/ref/hold.html?searchHighlight=hold%20on&s_tid=srchtitle_hold%20on_1