DL_1——自动求导、线性回归
文章目录
- 1 自动求导
-
- 1.1 向量链式法则
- 1.2 计算图
- 1.3 自动求导的两种模式
- 1.4 反向传播算法 bp
- 2 线性回归
-
- 2.1 模型假设
- 2.2 Loss Function 衡量预估质量
- 2.3 训练数据
- 2.4 参数学习
- 3 优化方法
-
- 3.1 梯度下降
- 3.2 小批量随机梯度下降
- 4 线性回归的从零实现
-
- 4.1 导入库
- 4.2 训练数据
- 4.3 定义模型
- 4.4 定义损失函数
- 4.5 定义优化方法
- 4.6 定义读取方式
- 4.7 完整代码
- 4.8 训练结果
- 5 简洁实现
-
- 完整代码
- 6 QA
1 自动求导
1.1 向量链式法则
- 标量链式法则
y = f ( μ ) , u = g ( x ) ∂ y ∂ x = ∂ y ∂ μ ∂ μ ∂ x y = f(\mu), u = g(x)\\ \frac{\partial y}{\partial x} = \frac{\partial y}{\partial \mu}\frac{\partial \mu}{\partial x} y=f(μ),u=g(x)∂x∂y=∂μ∂y∂x∂μ - 拓展到向量
∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x ∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x ∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x ( 1 , n ) ( 1 , ) ( 1 , n ) ( 1 , n ) ( 1 , k ) ( k , n ) ( m , n ) ( m , k ) ( k , n ) \begin{array}{c} \underset{\quad(1,n)(1,)(1,n)\quad(1,n)(1,k)(k,n)\quad(m,n)(m,k)(k,n)\quad }{\frac{\partial y}{\partial \mathbf{x}}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial \mathbf{x}}\quad \frac{\partial y}{\partial \mathbf{x}}=\frac{\partial y}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \mathbf{x}}\quad \frac{\partial \mathbf{y}}{\partial \mathbf{x}}=\frac{\partial \mathbf{y}}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \mathbf{x}} } \end{array} (1,n)(1,)(1,n)(1,n)(1,k)(k,n)(m,n)(m,k)(k,n)∂x∂y=∂u∂y∂x∂u∂x∂y=∂u∂y∂x∂u∂x∂y=∂u∂y∂x∂u
1.2 计算图
1.3 自动求导的两种模式
- 链式法则
∂ y ∂ x = ∂ y ∂ u n ∂ u n ∂ u n − 1 … ∂ u 2 ∂ u 1 ∂ u 1 ∂ x \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_{n}} \frac{\partial u_{n}}{\partial u_{n-1}} \ldots \frac{\partial u_{2}}{\partial u_{1}} \frac{\partial u_{1}}{\partial x} ∂x∂y=∂un∂y∂un−1∂un…∂u1∂u2∂x∂u1 - 正向积累
∂ y ∂ x = ∂ y ∂ u n ( ∂ u n ∂ u n − 1 ( … ( ∂ u 2 ∂ u 1 ∂ u 1 ∂ x ) ) ) \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_{n}}\left(\frac{\partial u_{n}}{\partial u_{n-1}}\left(\ldots\left(\frac{\partial u_{2}}{\partial u_{1}} \frac{\partial u_{1}}{\partial x}\right)\right)\right) ∂x∂y=∂un∂y(∂un−1∂un(…(∂u1∂u2∂x∂u1))) - 反向积累、反向传递、bp
∂ y ∂ x = ( ( ( ∂ y ∂ u n ∂ u n ∂ u n − 1 ) ⋯ ) ∂ u 2 ∂ u 1 ) ∂ u 1 ∂ x \frac{\partial y}{\partial x}=\left(\left(\left(\frac{\partial y}{\partial u_{n}} \frac{\partial u_{n}}{\partial u_{n-1}}\right) \cdots\right) \frac{\partial u_{2}}{\partial u_{1}}\right) \frac{\partial u_{1}}{\partial x} ∂x∂y=(((∂un∂y∂un−1∂un)⋯)∂u1∂u2)∂x∂u1
1.4 反向传播算法 bp
2 线性回归
以波士顿房价为例
2.1 模型假设
线性模型可以假设为: y = ⟨ w , x ⟩ + b y = \left \langle \mathbf{w}, \mathbf{x} \right \rangle + b y=⟨w,x⟩+b
线性模型可以看做一个单层的神经网络
输入层为 x i x_i xi,输出层为 y y y
2.2 Loss Function 衡量预估质量
设Loss为 ℓ ( y , y ^ ) = 1 2 ( y − y ^ ) 2 \ell(y, \hat{y}) = \frac{1}{2}(y-\hat{y})^2 ℓ(y,y^)=21(y−y^)2
所以: ℓ ( w , b ) = 1 2 ( ⟨ w , x ⟩ + b − y ^ ) 2 \ell(\mathbf{w}, b)=\frac{1}{2}(\left \langle \mathbf{w}, \mathbf{x} \right \rangle + b - \hat{y})^2 ℓ(w,b)=21(⟨w,x⟩+b−y^)2
2.3 训练数据
X = [ x 1 , x 2 , . . . , x n ] T \mathbf{X}=[\mathbf{x_1}, \mathbf{x_2}, ..., \mathbf{x_n}]^T X=[x1,x2,...,xn]T
Y = [ y 1 , y 2 , . . . , y n ] T \mathbf{Y}=[\mathbf{y_1}, \mathbf{y_2}, ..., \mathbf{y_n}]^T Y=[y1,y2,...,yn]T
2.4 参数学习
-
根据最优化,可得 w ∗ , b ∗ = arg min w , b ℓ ( w , b ) \mathbf{w}^*, b^*=\underset{\mathbf{w}, b}{\arg \min } \ell(\mathbf{w}, b) w∗,b∗=w,bargminℓ(w,b)
-
将bias加入weight
X ← [ X , 1 ] w ← [ w b ] ℓ ( w ) = 1 2 n ∥ y − X w ∥ 2 ∂ ∂ w ℓ ( w ) = 1 n ( y − X w ) T X \quad \mathbf{X} \leftarrow[\mathbf{X}, \mathbf{1}] \quad \mathbf{w} \leftarrow\left[\begin{array}{l}\mathbf{w} \\ b\end{array}\right]\\ \ell(\mathbf{w})=\frac{1}{2 n}\|\mathbf{y}-\mathbf{X} \mathbf{w}\|^{2} \frac{\partial}{\partial \mathbf{w}}\\ \ell(\mathbf{w})=\frac{1}{n}(\mathbf{y}-\mathbf{X} \mathbf{w})^{T} \mathbf{X} X←[X,1]w←[wb]ℓ(w)=2n1∥y−Xw∥2∂w∂ℓ(w)=n1(y−Xw)TX -
Loss是凸函数,满足:
∂ ∂ w ℓ ( w ) = 0 ⇔ 1 n ( y − X w ) T X = 0 ⇔ w ∗ = ( X T X ) − 1 X T y \begin{array}{c} \frac{\partial}{\partial \mathbf{w}} \ell(\mathbf{w})=0 \\ \Leftrightarrow \frac{1}{n}(\mathbf{y}-\mathbf{X} \mathbf{w})^{T} \mathbf{X}=0 \\ \Leftrightarrow \mathbf{w}^{*}=\left(\mathbf{X}^{T} \mathbf{X}\right)^{-1} \mathbf{X}^T \mathbf{y} \end{array} ∂w∂ℓ(w)=0⇔n1(y−Xw)TX=0⇔w∗=(XTX)−1XTy
3 优化方法
3.1 梯度下降
w t = w t − 1 − η ∂ ℓ ∂ w t − 1 \mathbf{w}_{t}=\mathbf{w}_{t-1}-\eta \frac{\partial \ell}{\partial \mathbf{w}_{t-1}} wt=wt−1−η∂wt−1∂ℓ
3.2 小批量随机梯度下降
- 在整个训练集上算梯度开销太大
- 我们可以随机采样b个样本 i 1 , i 2 , i 3 , . . . , i b i_1,i_2,i_3,...,i_b i1,i2,i3,...,ib来近似损失
1 b ∑ i ∈ I b ℓ ( x i , y i , w ) \frac{1}{b} \sum_{i \in I_{b}} \ell\left(\mathbf{x}_{i}, y_{i}, \mathbf{w}\right) b1i∈Ib∑ℓ(xi,yi,w)
其中,b是批量大小,超参数
4 线性回归的从零实现
4.1 导入库
import random
import numpy as np
import torch
from d2l import torch as d2l
import math
4.2 训练数据
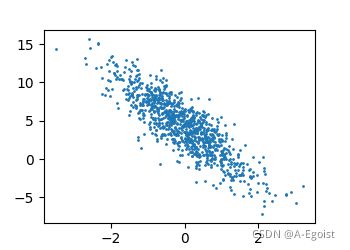
生成X.shape=(1000, 2), y.shape=(1000, 1)的数据集
def synthetic_data(w, b, num_examples):
X = torch.normal(0, 1, (num_examples, len(w))) # 构建一个服从均值为0,标准差为1的正态分布随机数
y = torch.matmul(X, w) + b # 矩阵乘法
y += torch.normal(0, 0.01, y.shape) # 加入随机噪声
return X, y.reshape((-1, 1)) # y变为列向量
if __name__ == '__main__':
true_w = torch.tensor([2, -3.4])
true_b = 4.2
# 生成X.shape=(1000, 2)
# y.shape=(1000, 1)的数据集
features, labels = synthetic_data(true_w, true_b, 1000)
print(f'features:{
features}, labels:{
labels}')
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
d2l.plt.show()
4.3 定义模型
def liner_regression(X, w, b):
'''线性模型'''
return torch.matmul(X, w) + b
4.4 定义损失函数
采用MSE
def squared_loss(y_hat, y):
'''均方损失'''
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
4.5 定义优化方法
采用MSGD
def sgd(params, lr, batch_size):
'''小批量随机梯度下降'''
with torch.no_grad():
# 在该模块下,所有计算得出的tensor的requires_grad都自动设置为False
for param in params:
param -= lr * param.grad / batch_size # 更新参数
param.grad.zero_() # 梯度清空
4.6 定义读取方式
使用小批量读取的方式
def data_iterator(batch_size, features, labels):
'''小批量读取数据'''
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
4.7 完整代码
import random
import numpy as np
import torch
from d2l import torch as d2l
import math
def synthetic_data(w, b, num_examples):
'''生成数据'''
X = torch.normal(0, 1, (num_examples, len(w))) # 构建一个服从均值为0,标准差为1的正态分布随机数
y = torch.matmul(X, w) + b # 矩阵乘法
y += torch.normal(0, 0.01, y.shape) # 加入随机噪声
return X, y.reshape((-1, 1)) # y变为列向量
def data_iterator(batch_size, features, labels):
'''小批量读取数据'''
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
def liner_regression(X, w, b):
'''线性模型'''
return torch.matmul(X, w) + b
def squared_loss(y_hat, y):
'''均方损失'''
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
def sgd(params, lr, batch_size):
'''小批量随机梯度下降'''
with torch.no_grad():
# 在该模块下,所有计算得出的tensor的requires_grad都自动设置为False
for param in params:
param -= lr * param.grad / batch_size # 更新参数
param.grad.zero_() # 梯度清空
if __name__ == '__main__':
true_w = torch.tensor([2, -3.4])
true_b = 4.2
# 生成X.shape=(1000, 2)
# y.shape=(1000, 1)的数据集
features, labels = synthetic_data(true_w, true_b, 1000) # 生成特征和标签
# d2l.set_figsize()
# d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)
# d2l.plt.show()
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True) # 随机设定初始weight
b = torch.zeros(1, requires_grad=True) # 随机设定初始bias
batch_size = 10 # 批量大小
lr = 0.03 # 学习率
num_epochs = 3 # 训练批次
net = liner_regression # model
loss = squared_loss # loss
for epoch in range(num_epochs):
# 每一轮的训练过程
for X, y in data_iterator(batch_size, features, labels):
l = loss(net(X, w, b), y)
l.sum().backward()
sgd([w, b], lr, batch_size)
# 每训练一轮输出训练结果
with torch.no_grad():
train_loss = loss(net(features, w, b), labels)
print(f'epoch {
epoch}, loss {
float(train_loss.mean()):f}')
print(f'w的真实值: {
true_w}')
print(f'w的估计值: {
w.reshape(true_w.shape)}')
print(f'w的估计误差: {
true_w - w.reshape(true_w.shape)}')
print(f'b的真实值: {
true_b}')
print(f'b的估计值: {
b}')
print(f'b的估计误差: {
true_b - b}')
4.8 训练结果
epoch 0, loss 0.038375
epoch 1, loss 0.000145
epoch 2, loss 0.000053
w的真实值: tensor([ 2.0000, -3.4000])
w的估计值: tensor([ 1.9994, -3.3986], grad_fn=
w的估计误差: tensor([ 0.0006, -0.0014], grad_fn=
b的真实值: 4.2
b的估计值: tensor([4.1994], requires_grad=True)
b的估计误差: tensor([0.0006], grad_fn=
5 简洁实现
完整代码
# -*- coding: utf-8 -*-
# @Time : 2021/9/11 11:28
# @Author : Amonologue
# @software : pycharm
# @File : liner_regression_simple.py
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nn
def load_array(data_arrays, batch_size, is_train=True):
'''一个构造PyTorch数据迭代器'''
dataset = data.TensorDataset(*data_arrays)
return data.DataLoader(dataset, batch_size, shuffle=is_train)
if __name__ == '__main__':
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000) # 利用封装好的数据生成器
batch_size = 10
data_iterator = load_array((features, labels), batch_size) # 构造PyTorch数据迭代器
net = nn.Sequential(nn.Linear(2, 1)) # 定义一个线性回归的模型, 并将其放在PyTorch容器中
net[0].weight.data.normal_(0, 0.01) # 随机设置weight初始值
net[0].bias.data.fill_(0) # 设置bias初始值
print(net[0].weight.data)
print(net[0].bias.data)
loss = nn.MSELoss() # 定义MSE损失函数
trainer = torch.optim.SGD(net.parameters(), lr=0.03) # 定义SGD优化
num_epochs = 3 # 设置训练轮次
for epoch in range(num_epochs):
for X, y in data_iterator:
l = loss(net(X), y)
trainer.zero_grad() # 梯度清零
l.backward()
trainer.step() # 更新参数
l = loss(net(features), labels) # 计算loss
print(f'epcoh: {
epoch}, loss {
l:f}')
print(f'w的真实值: {
true_w}')
print(f'w的估计值: {
net[0].weight.data}')
print(f'w的估计误差: {
true_w - net[0].weight.data.reshape(true_w.shape)}')
print(f'b的真实值: {
true_b}')
print(f'b的估计值: {
net[0].bias.data}')
print(f'b的估计误差: {
true_b - net[0].bias.data}')
6 QA
- Q: 为什么使用均方损失而不是绝对差值
A: 因为绝对差值不可导 - Q:batchsize的大小是否会影响模型结果
A: - Q:
A: - Q:
A: - Q:
A: