深度学习——反向传播(Backpropagation)
反向传播算法(Backpropagation)
文章目录
- 反向传播算法(Backpropagation)
-
- 一.简介
- 二.反向传播原理
-
- 2.1 导数的链式法则
- 2.2 正向传播与反向传播
- 三.总结
一.简介
无论是机器学习,还是深度学习。都绕不开一个梯度下降。在进行深度学习简介的时候,我们有介绍过深度学习的大致步骤,分别为:
- 构建神经网络
- 数据拟合
- 选出最佳模型
其中,选出最佳模型的方式,其实就是利用梯度下降算法,选出损失函数最小的那个。在传统的机器学习当中,这个比较容易,直接算就行了。但是在深度学习当中,由于存在输入层,隐藏层,输出层,且隐藏层到底有多深,这些都是未知数,因此计算也会更加繁杂。
如果,在输出层输出的数据和我们设定的目标以及标准相差比较大,这个时候,就需要反向传播。利用反向传播,逐层求出目标函数对各神经元权值的偏导数,构成目标函数对权值向量的梯度,之所以算这个,是为了对权值的优化提供依据,等权值优化了之后,再转为正向传播……当输出的结果达到设定的标准时,算法结束。
二.反向传播原理
2.1 导数的链式法则
反向传播的基本原理其实不难,基本理论就是大学高等数学当中的导数计算。我们需要了解的就是链式法则:
若 y = g ( x ) , z = h ( y ) , 则 : d z d x = d z d y d y d x 若y=g(x), z = h(y),则:\\ \frac{dz}{dx} = \frac{dz}{dy}\frac{dy}{dx} 若y=g(x),z=h(y),则:dxdz=dydzdxdy
若 x = g ( s ) , y = h ( s ) , z = k ( x , y ) , 则 : d z d s = d z d x d x d s + d z d y d y d s 若x=g(s),y=h(s),z=k(x,y),则:\\ \frac{dz}{ds} = \frac{dz}{dx}\frac{dx}{ds} + \frac{dz}{dy}\frac{dy}{ds} 若x=g(s),y=h(s),z=k(x,y),则:dsdz=dxdzdsdx+dydzdsdy
2.2 正向传播与反向传播
我们还是用逻辑回归的神经元为例:
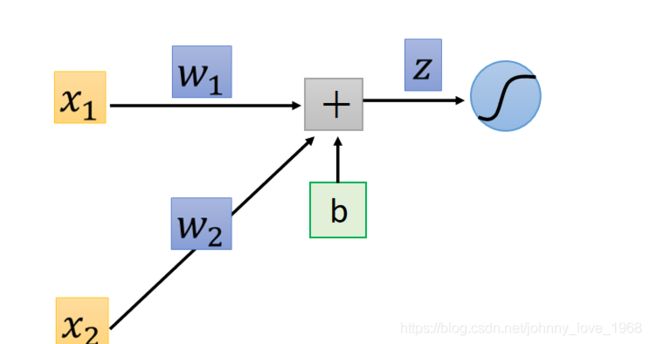
很显然,在这神经元当中z = w1x1+w2x2 + b。最后,这个线性方程z会被代入到Sigmoid函数当中,也就是说:
S i g m o i d 函 数 : a = σ ( z ) Sigmoid函数:a = \sigma(z) Sigmoid函数:a=σ(z)
我们知道,无论是机器学习,还是深度学习,计算之后都会产生一定的损失值,我们把这个损失函数记为l。
在一部分当中,我们有说过,反向传播的最终目的是修正权值w,那么我们让l对w求偏导,根据链式准则:
∂ l ∂ w = ∂ z ∂ w ∂ l ∂ z ( 公 式 0 ) \frac{\partial l}{\partial w} = \frac{\partial z}{\partial w}\frac{\partial l}{\partial z}(公式0) ∂w∂l=∂w∂z∂z∂l(公式0)
其中,z对w求偏导这一步其实不难,不就是z对w求导嘛,我们很容易就能算出:
∂ z ∂ w 1 = x 1 , ∂ z ∂ w 2 = x 2 \frac{\partial z}{\partial w_{1}} = x_{1},\frac{\partial z}{\partial w_{2}} = x_{2} ∂w1∂z=x1,∂w2∂z=x2
而x1,x2其实就是最开始的输入值,因此可以当做是已知的。上面这个计算过程,就是正向传播
而l对z求导,这个部分其实很复杂。这一部分的求解过程,就是反向传播。那么这个部分该怎么求呢?如下所示:
∂ l ∂ z = ∂ a ∂ z ∂ l ∂ a = σ ′ ( z ) ∂ l ∂ a ( 公 式 1 ) \frac{\partial l}{\partial z} = \frac{\partial a}{\partial z}\frac{\partial l}{\partial a} = \sigma '(z)\frac{\partial l}{\partial a}(公式1) ∂z∂l=∂z∂a∂a∂l=σ′(z)∂a∂l(公式1)
如果这个神经网络稍微复杂一点呢?比如说,像下面这样:
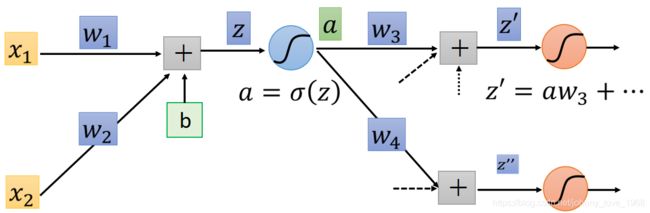
那么,我们根据链式法则,就可以得到:
∂ l ∂ a = ∂ z ′ ∂ a ∂ l ∂ z ′ + ∂ z ′ ′ ∂ a ∂ l ∂ z ′ ′ = w 3 ∂ l ∂ z ′ + w 4 ∂ l ∂ z ′ ′ \frac{\partial l}{\partial a} = \frac{\partial z'}{\partial a}\frac{\partial l}{\partial z'} + \frac{\partial z''}{\partial a}\frac{\partial l}{\partial z''} = w_{3}\frac{\partial l}{\partial z'} + w_{4}\frac{\partial l}{\partial z''} ∂a∂l=∂a∂z′∂z′∂l+∂a∂z′′∂z′′∂l=w3∂z′∂l+w4∂z′′∂l
上面这个式子与公式1结合,就是:
∂ l ∂ z = σ ′ ( z ) [ w 3 ∂ l ∂ z ′ + w 4 ∂ l ∂ z ′ ′ ] ( 公 式 2 ) \frac{\partial l}{\partial z} = \sigma '(z)[w_{3}\frac{\partial l}{\partial z'} + w_{4}\frac{\partial l}{\partial z''}](公式2) ∂z∂l=σ′(z)[w3∂z′∂l+w4∂z′′∂l](公式2)参考下面这个图看一看
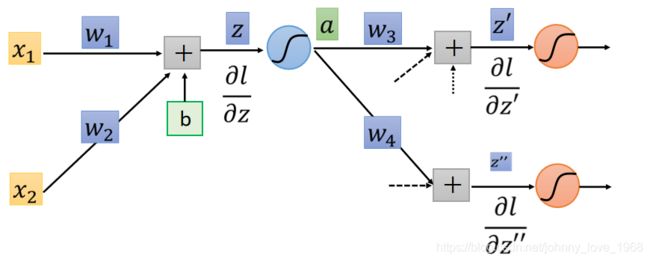
如此一来,反向传播的这一部分,我们也知道了求解原理。
对于公式2的方式,人们梳理了一下这个过程像极了如下所示的这个流程。即:先求l对z’的导,以及l对z’‘的导,然后分别乘以w3和w4,在结合sigma’(z),于是有人就根据这个计算流程,画出来了下面这个图:
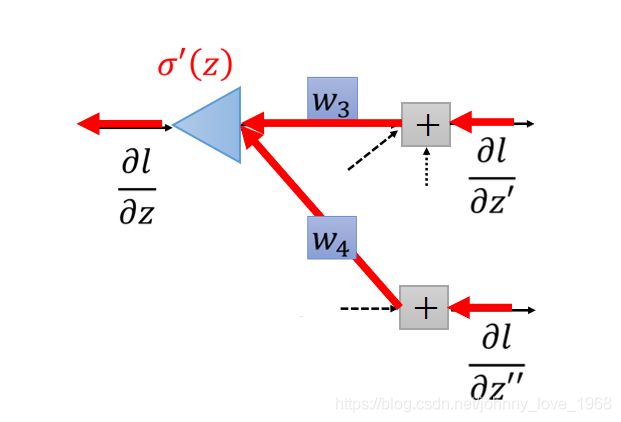
这其实不就是我们所举的这个神经网络,把箭头全都倒过来嘛。因此,便有了“反向传播”的说法。
这当中,我们注意红色标注的sigma’(z),这个是Simoid函数对z进行求导的结果。由于在正向传播的时候,z是什么其实已经知道了,sigomid函数我们也是知道的,因此sigma’(z)我们也是已知的。
不过,又产生新的问题了。dl/dz的求解,明显依赖于dl/dz’,以及dl/dz’’。那么这两项又是如何求的呢?答案是:根据输出值去求。任何一组数据,在经过神经网络运算之后,都会产生一个输出值,我们记为y。如下所示:
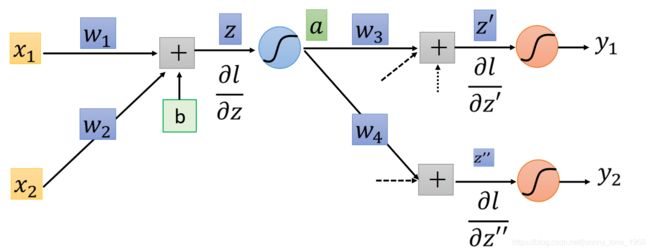
这个时候,我们就要分情况讨论了。
- 第一种情况:y1与y2在都在输出层
这个时候,比较简单,根据下面这个公式,直接套用即可:
∂ l ∂ z ′ = ∂ y 1 ∂ z ′ ∂ l ∂ y 1 ∂ l ∂ z ′ ′ = ∂ y 2 ∂ z ′ ′ ∂ l ∂ y 2 \frac{\partial l}{\partial z'} = \frac{\partial y_{1}}{\partial z'}\frac{\partial l}{\partial y_{1}} \\ \frac{\partial l}{\partial z''} = \frac{\partial y_{2}}{\partial z''}\frac{\partial l}{\partial y_{2}} ∂z′∂l=∂z′∂y1∂y1∂l∂z′′∂l=∂z′′∂y2∂y2∂l - 第二种情况:y1,y2存在不在输出层的情况
这个时候,那就一直算到输出层,然后再从输出层往回传播即可。
关于这部分的一些细节问题,看反向传播补充
这里的细节,主要体现在l到底是什么,又是如何求导的。
三.总结
正向传播与反向传播其实是同时使用的。
首先,你需要正向传播,来计算z对w的偏导,进而求出sigmoid’(z)是多少。然后,根据输出层输出的数据进行反向传播,计算出l对z的偏导是多少,最后,代入到公式0当中,即可求出l对w的偏导是多少。注意,这个偏导,其实反应的就是梯度。然后我们利用梯度下降等方法,对这个w不断进行迭代(也就是权值优化的过程),使得损失函数越来越小,整体模型也越来越接近于真实值。