自动控制原理复习——线性系统的根轨迹法

        我们知道线性系统的性能与闭环函数的极点分布有很大关系，当闭环函数的极点全部位于s左平面时，系统是稳定的，当闭环函数的极点都是实数且无零点的情况下，系统单位阶跃响应曲线是单调的，当闭环函数的极点是共轭复数根时，系统响应通常是振荡的。所以在分析一个系统的特性时确定闭环函数的极点位置分布是很有必要的，但是闭环函数极点的位置通常难以确定，且随着系统的某一参数变化而变化，但是开环函数的零极点是较容易确认的，因为开环传递函数往往是由一些低阶环节以串联方式连接而成的。而根轨迹法就是通过开环函数的零极点来确认闭环极点随着某一参数变化的变化规律。

 目录

1.根轨迹法的基本概念

      1.1什么叫根轨迹

      1.2 根轨迹与系统性能关系

        1.2.1 稳定性

        1.2.2稳态特性

        1.2.3动态特性

        1.3根轨迹方程以及幅角、幅值条件

        1.3.1 根轨迹方程

        

        1.3.2 幅角、幅值条件

2.绘制根轨迹的基本规则

        2.1 根轨迹的分支数、对称性与连续性

        2.2 根轨迹的起点和终点

        2.3 根轨迹在实轴上的分布

        2.4 根轨迹的渐进线

        2.5 根轨迹的分离会合点和分离会合角

        2.5.1 根轨迹分离点与会合点的计算方法

        2.5.2 根轨迹的分离角或会合角的计算公式

        2.6 根轨迹与虚轴的交点

        2.7 根轨迹的出射角和入射角

        2.8 特征方程根的和

3.广义根轨迹

        3.1 参数根轨迹

        3.2 零度根轨迹

4.控制系统的根轨迹分析

        4.1 利用闭环主导极点估算系统的性能

        4.2闭环偶极子对根轨迹的影响

        4.3附加开环零点的影响

        4.4附加开环极点的影响

5.基于根轨迹的PID控制器设计

1.根轨迹法的基本概念

      1.1什么叫根轨迹

        根轨迹是指当开环系统某个参数由零变化到无穷大时，闭环系统特征根在s平面上移动的轨迹。

      1.2 根轨迹与系统性能关系

        1.2.1 稳定性

        当参数由零变化到无穷时，根轨迹不会越过虚轴进入s右半平面则说明系统对于所有的K值都是稳定的，如果根轨迹越过虚轴进入s右半平面，则系统进入不稳定的状态。

        1.2.2稳态特性

        一般情况下，根轨迹图上标注的参数不是开环增益而是根轨迹增益，根轨迹增益与稳态误差系数之间仅相差一个比例常数，

        1.2.3动态特性

        当所有闭环极点都位于实轴上，系统为过阻尼系统，当极点重合时，系统为临界Zune系统，当闭环极点为共轭复数极点，系统为欠阻尼系统，单位阶跃响应是衰减振荡过程，切超调量将随着K值的增大而增大。

        1.3根轨迹方程以及幅角、幅值条件

        1.3.1 根轨迹方程

        

             

        

        这是一个向量方程，代表的是一个向量。

        1.3.2 幅角、幅值条件

        幅值条件：

        

        幅角条件：

       

        满足幅角条件和幅值条件的复数s，就是在给定参数K值下系统的闭环特征方程的根但参数K就从变化的，所以只要满足幅角条件的点s都在根轨迹上，所以幅角条件是确认复平面上根轨迹的充分必要条件。

2.绘制根轨迹的基本规则

        2.1 根轨迹的分支数、对称性与连续性

        根轨迹的分支数N=max{开环零点数m，开环极点数n}，根轨迹关于实轴对称且连续

        2.2 根轨迹的起点和终点

        根轨迹的起点是当参数K=0的时候闭环极点的位置，这时候特征方程为

        ，所以根轨迹的起点是开环函数的极点。

        根轨迹的终点是当参数是闭环极点的位置，这时候特征方程近似为

        ，所以根轨迹的终点是开环函数的零点

        综上，根轨迹起于开环极点终于开环零点。

        若开环极点数n大于开环零点数m，起于极点数的n条中有m条会终于m个开环零点，剩余的n-m条根轨迹会起于开环极点，沿着n-m条渐进线趋向于无限零点

        2.3 根轨迹在实轴上的分布

        根轨迹方程为，共轭复数根不会对G(s)H(s)的幅角有影响，实轴上的一个点s，s左边的零极点到s的幅角为0，右边的是，要让幅角为(2k+1)，只需要满足s右侧开环零点极点数目之和为奇数即可。

    实轴上的某一区域，如果其右侧的开环极点与开环零点的数目之和为奇数，则该区域必是根轨迹

        2.4 根轨迹的渐进线

        渐进线的条数为(n-m),n是开环极点个数，m是开环零点个数；

        渐进线的角度为：

        

        渐进线与实轴的交点为：

        

        2.5 根轨迹的分离会合点和分离会合角

        如果根轨迹在两个相邻的极点之间则至少存在一个分离点，如果根轨迹在两个相邻的零点之间则至少存在一个会合点。

        2.5.1 根轨迹分离点与会合点的计算方法

        

        ,求出来的s点就是分离会合点的坐标。通常分离会合点是复重根。

        2.5.2 根轨迹的分离角或会合角的计算公式

        ，是根轨迹的条数，等于n-m.

        2.6 根轨迹与虚轴的交点

        可以通过特征方程的劳斯表求出存在全零行的值，再通过辅助方程求出与虚轴的交点。

        2.7 根轨迹的出射角和入射角

        根轨迹离开开环复数极点处的切线方向与实轴正方向的夹角为出射角，而进入开环复数零点处的切线方向与实轴正方向的夹角为入射角，为了比较精确地绘制根轨迹在起点和终点附近的基本形状，需要求出这些入射角和出射角。

        设有一对共轭极点,,一个零点,在处无限接近的点设为,由幅角公式：

        

        处的出射角为

       处的出射角

        零点处的入射角同理可以通过幅角公式求得。

        2.8 特征方程根的和

        由特征方程得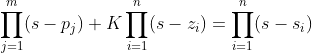,展开得标准形式，当  时比较第二项系数可以得到：

        

       即闭环特征根之和会等于开环极点之和。

3.广义根轨迹

  上面我们控制变化的参数仅仅是开环增益，但我们常常还要研究系统其他参数变化对闭环特征根的影响，在有些系统中还会遇到正反馈的情况，当开环函数中中还有纯延迟环节是根轨迹的方法也不一样，通常将这些根轨迹统称为广义根轨迹。

        3.1 参数根轨迹

        当我们要研究参数A对系统闭环极点的影响时，我们可以吧闭环特征方程中含A的各项合并，闭环特征方程整理为：

        

方程两边同时除以Q(s)：

        

 得到等效开环传递函数：

        

然后根据根轨迹绘制法则绘制出关于参数A的根轨迹即可。

        3.2 零度根轨迹

        当系统的反馈环节时正反馈时，系统的特征方程就变成：

        

        这时候幅值条件不变但幅角条件变为：

        

        这种系统的根轨迹就叫做零度根轨迹，在运用根轨迹绘制法则时需要更改一些条件：

        法则3 根轨迹在实轴上的分布条件改为：实轴上的某一区域，若其右侧开环零点数目之和为偶数，则该区域必是根轨迹

        法则4 根轨迹渐进线的夹角改为：

        法则7 根轨迹的入射角与出射角

        设有一对共轭极点,,一个零点,在处无限接近的点设为,由幅角公式：

        

        处的出射角为

       处的出射角

4.控制系统的根轨迹分析

        4.1 利用闭环主导极点估算系统的性能

        在s左半平面靠近虚轴且附近无闭环零点的闭环极点对系统性能的影响最大，称为系统的闭环主导极点，比主导极点实部大5倍以上的闭环零点极点可以忽略，在一般情况下，高阶系统的设计都以获得衰减振荡响应过程为最满意的设计，因此闭环主导极点通常是一对共轭复数极点，相应的高阶系统可以简化为二阶系统进行分析

        4.2闭环偶极子对根轨迹的影响

        如果系统在s左半平面有一对相距很近的闭环零点极点，且他们之间的距离比他们的幅值小一个数量级时，这一对闭环零点、极点称为闭环偶极子，当偶极子不十分接近坐标原点时，他们可以被忽略不计，当偶极子靠近原点时，他们的影响则不可忽略。

        4.3附加开环零点的影响

        在实际系统中，只调整增益往往不能获得期望的系统性能，还需要增加闭环零点获闭环极点，由于根轨迹是由开环零点、极点决定的，因此在系统中增加零极点或者改变零极点的位置，会改变根轨迹的形状。

        在开环传递函数上增加负实部零点会让根轨迹向左方移动，从而增加系统的稳定性，减小系统响应的调整时间。

        4.4附加开环极点的影响

        在开环传递函数中增加极点，可以使根轨迹向右移动，导致系统的稳定性降低，响应时间增加

5.基于根轨迹的PID控制器设计

---