'''
Linear Discriminant Analysis (LDA) in manuer and scikit-learn
1. Calculate mean vectors of each class
2. Calculate within-class and between-class scatter matrices
3. Calculate eigenvalues and eigenvectors for
4. Keep the top k eigenvectors by ordering them by descending eigenvalues
5. Use the top eigenvectors to project onto the new space
'''
# import the Iris dataset from scikit-learn
from sklearn.datasets import load_iris
# import our plotting module
import matplotlib.pyplot as plt
# load the Iris dataset
iris = load_iris()
# 创建X,y变量来表示特征和响应变量列。create X and y variables to hold features and response column
iris_X, iris_y = iris.data, iris.target
# calculate the mean for each class
mean_vectors = []
for cl in [0, 1, 2]:
class_mean_vector = np.mean(iris_X[iris_y==cl], axis=0)
mean_vectors.append(class_mean_vector)
print( label_dict[cl], class_mean_vector)
# Calculating within-class and between-class scatter matrices
# Calculate within-class scatter matrix
S_W = np.zeros((4,4))
# for each flower
for cl,mv in zip([0, 1, 2], mean_vectors):
# scatter matrix for every class, starts with all 0's
class_sc_mat = np.zeros((4,4))
# for each row that describes the specific flower
for row in iris_X[iris_y == cl]:
# make column vectors
row, mv = row.reshape(4,1), mv.reshape(4,1)
# this is a 4x4 matrix
class_sc_mat += (row-mv).dot((row-mv).T)
# sum class scatter matrices
S_W += class_sc_mat
S_W
# calculate the between-class scatter matrix
# mean of entire dataset
overall_mean = np.mean(iris_X, axis=0).reshape(4,1)
# will eventually become between class scatter matrix
S_B = np.zeros((4,4))
for i,mean_vec in enumerate(mean_vectors):
# number of flowers in each species
n = iris_X[iris_y==i,:].shape[0]
# make column vector for each specied
mean_vec = mean_vec.reshape(4,1)
S_B += n * (mean_vec - overall_mean).dot((mean_vec - overall_mean).T)
S_B
#Calculating eigenvalues and eigenvectors for SW-1SB
# calculate eigenvalues and eigenvectors of S−1W x SB
eig_vals, eig_vecs = np.linalg.eig(np.dot(np.linalg.inv(S_W), S_B))
eig_vecs = eig_vecs.real
eig_vals = eig_vals.real
for i in range(len(eig_vals)):
eigvec_sc = eig_vecs[:,i]
print ('Eigenvector {}: {}'.format(i+1, eigvec_sc))
print ('Eigenvalue {:}: {}'.format(i+1, eig_vals[i]))
print()
# keep the top two linear discriminants
linear_discriminants = eig_vecs.T[:2]
linear_discriminants
#explained variance ratios
eig_vals / eig_vals.sum()
# LDA projected data
lda_iris_projection = np.dot(iris_X, linear_discriminants.T)
# plot
label_dict = {i: k for i, k in enumerate(iris.target_names)}
def plot(X, y, title, x_label, y_label):
ax = plt.subplot(111)
for label,marker,color in zip(range(3),('^', 's', 'o'),('blue', 'red', 'green')):
plt.scatter(x=X[:,0].real[y == label],y=X[:,1].real[y == label],color=color,alpha=0.5,label=label_dict[label])
plt.xlabel(x_label)
plt.ylabel(y_label)
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title(title)
plt.show()
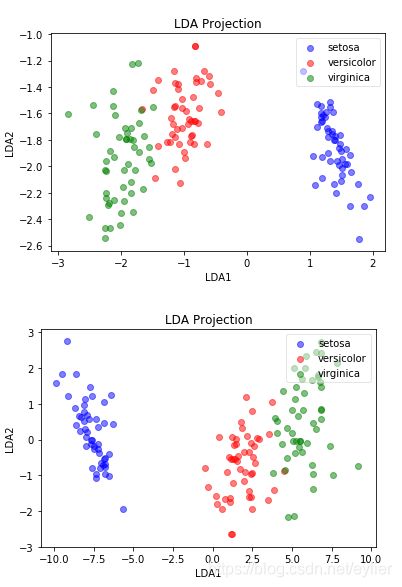
plot(lda_iris_projection, iris_y, "LDA Projection", "LDA1", "LDA2")
#How to use LDA in scikit-learn
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# instantiate the LDA module
lda = LinearDiscriminantAnalysis(n_components=2)
# fit and transform our original iris data . LDA is supervised clssifier
X_lda_iris = lda.fit_transform(iris_X, iris_y)
lda.scalings_
lda.explained_variance_ratio_
'''scikit学习线性判别式对特征向量进行了标准化缩放,它们都是有效的特征向量。唯一的区别是投影数据的缩放'''
# plot the projected data
plot(X_lda_iris, iris_y, "LDA Projection", "LDA1", "LDA2")