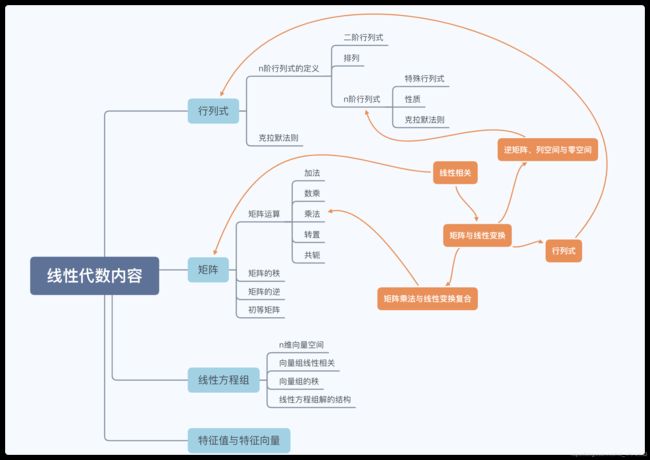
关于线性代数本质的学习笔记

关于线性代数本质的学习

下面的内容来自bilibili线性代数的本质视频，是我看视频和结合现代知识之后的总结。
视频连接 https://www.bilibili.com/video/BV1Ys411k7yQ?share_source=copy_web

线性相关

有多个向量，并且可以移除其中一个而不减小张成的空间，这种情况发生时就称它们是“线性相关”的；或者说其中一个向量可以表示为其它向量的线性组合。

矩阵与线性变换

线性变换是一种操纵空间的手段，如果我们把一个平面直角坐标系看作无数个正方形网格的组合，那么线性变换始终使网格线保持平行并等距分布，且原点不变。由于每一个平面都可以用一组基向量来表示，因此我们可以用一个2x2矩阵来记录变换后的空间。因此对于每一个矩阵，都可以把它理解为对空间的一种特定变换。
矩阵向量乘法就是计算线性变化作用于给定向量的一种途径

对于上式的矩阵向量乘法，我们可以把前一个矩阵的列看作目标空间基向量的坐标（即平面直角坐标系经过线性变换得到的新空间），把后一个向量看作是需要变换的点在原空间的坐标，它们相乘之后就得到了该点在目标空间的坐标。我们可以把上述过程理解为**[线性变换][输入向量]=[输出向量]**

矩阵乘法与线性变换复合

如果是两个矩阵相乘，我们就可以理解为两种线性变换的叠加。如上图，我们把M1看作一个线性变换，它的两个基向量分别为i(e,g), j(f,h)。在线性变换M1上叠加M2变换就可以理解为线性变换M2分别作用于M1的两个基向量，也就是说把两个矩阵相乘分解为两个上述的矩阵向量乘法。右边矩阵的第一列就是M1的基向量i经过M2变换，第二列就是M1的基向量j经过M2变换。
上文中我们把矩阵向量乘法理解为一种函数[线性变换][输入向量]=[输出向量]，对于矩阵乘法我们同样可以这样理解[线性变换][输入矩阵]=[输出矩阵]。函数的一般写法是将函数放在左边，自变量放在右边，如f(g(x))，因此矩阵的乘法也是同样的形式。于是我们很容易就可以判断出矩阵乘法一般不满足交换律，因为矩阵乘法的本质是函数作用于自变量，而非代数乘法。我们也可以很快得到结论，矩阵乘法满足结合律。

行列式

如果我们把目光聚焦于平面直角坐标系中一个1x1的小方格，它的面积是1，那么线性变换的行列式就可以理解为小方格的面积经过线性变换后得到的新的小方格的面积是原来面积的多少倍。当线性变换的行列式为0时，说明该线性变换将平面压缩成为了一条直线或者一个点。如果我们把一个二维平面想象成为一张纸，初始时正面向上，如果经过线性变换后这张纸变成了反面向上，我们就认为该平面的空间取向被翻转了（也可以用基向量i,j来理解，初始时j在i左边，翻转后j在i右边）。当行列式出现负值时，我们就认为空间取向被翻转了，行列式的绝对值依旧表示面积的缩放比例。
对于三维空间的行列式，我们可以理解为体积的变化。三维空间的空间取向我们可以用右手定则来定义，如果线性变换后不能使用右手定则，则说明空间取向被翻转了。

逆矩阵、列空间与零空间

我们使用逆矩阵来计算线性方程组Ax=v的解，给该式两端分别左乘A-1，即A-1Ax=A-1v，就得到了x=A-1v
当行列式为0时，矩阵不存在逆变换，因为线性变换不能把一条直线复原成一个平面或者把一个点复原成一个三维空间。但是当行列式为0时，解仍然可能存在，比如当一个平面被压缩为一条直线时，如果v在这条直线上，则存在解。
秩（rank）代表变换后空间的维数，矩阵的列可以看作变换后空间的基向量，列空间就是列向量张成当空间。更准确的说，秩代表列空间的维数。当秩为最大值时，秩与列数相等，我们就称为满秩。
如果一个二维平面在变换后变成一条直线，那必然有一个方向上的向量全部落在原点上。变换后落在原点的向量的集合被称为所选矩阵的“零空间”或“核”。对线性方程组Ax=v来说，当向量v恰好为零向量时（齐次线性方程组），零空间给出的就是这个向量方程的所有可能解。

点积与对偶性

将向量放倒，得到与之相关的矩阵

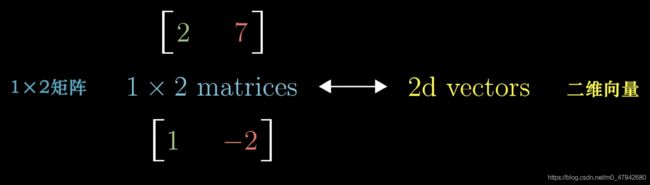
或者将矩阵直立，得到与之相关的向量

通过线性变换，我们可以把一个二维空间变换成一条直线，或者说数轴，只是此时所有基向量都落在了一个数上。那么矩阵[a,b]就可以看作是一个二维空间[i,j]变换后的样子，只是此时每一列的数都是一个新的“基向量”（a表示数字，i表示向量）。也就是说我们可以把点积改写为矩阵向量乘积的形式，即**[线性变换][输入向量]=[输出向量]**，而这个乘法的结果就是点积的结果。

叉乘

对于两个三维向量的叉乘，它的数值计算方法如下，方向由右手定则来确定

我们下面来考虑三维向量叉乘的几何意义。在对于点积几何意义的探索中，我们用到了对偶性，这是将点积与线性变换进行相互转换的关键点。

对于一个从多维空间变换到数轴的线性变换 [一维矩阵] 来说，它具有对偶性。也就是说，对于一个向量做这样的线性变换，与将此矩阵竖起来与该向量做点乘是等价的。

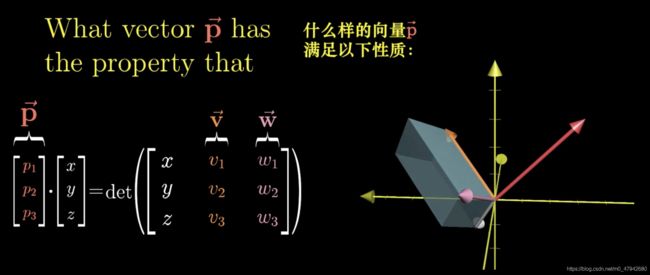
因此我们用同样的方法来探索叉乘的意义。两个二维向量i，j的叉乘是一个新的向量z，大小是两个向量组成的平行四边形的面积，方向则由右手定则来确定。而对于两个三维向量来说，它们的叉乘的大小并不是一个确定的数值。因为三维向量的叉乘是由两个向量v，w进行的，它的数值是一个以vw组成的平行四边形为底面，以变化的向量a到地面的长度为高的平行六面体的体积，它的方向也由右手定则来确定。
因此我们从三维变量叉乘的计算方法中去定义一个p，这个向量p的转置就是一个从三维空间到数轴的线性变换，而这个变幻将变化的向量a投影到与vw平面垂直的数轴上。向量a（x，y，z）经过线性变换p得到的新的向量就是数轴上的一个数。

基变换

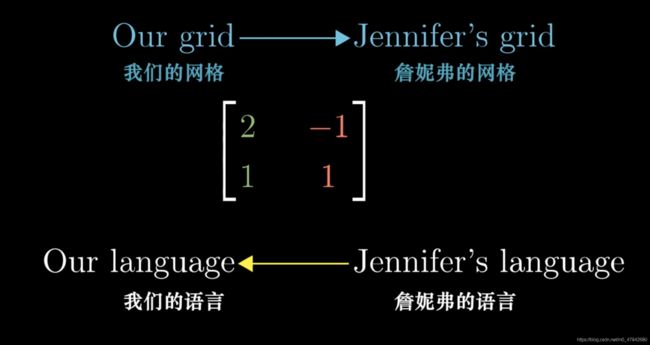
对于一个基变换，比如我们令x（2，1）y（-1，1）为一个新的坐标系的基向量，这个坐标系在我们原本的坐标系中就用一个上述的矩阵来表示。从几何上讲，这个矩阵是用我们的网络来表示jen的网络，但是从数值上讲这是用jen的语言描述转化为用我们的语言来描述。

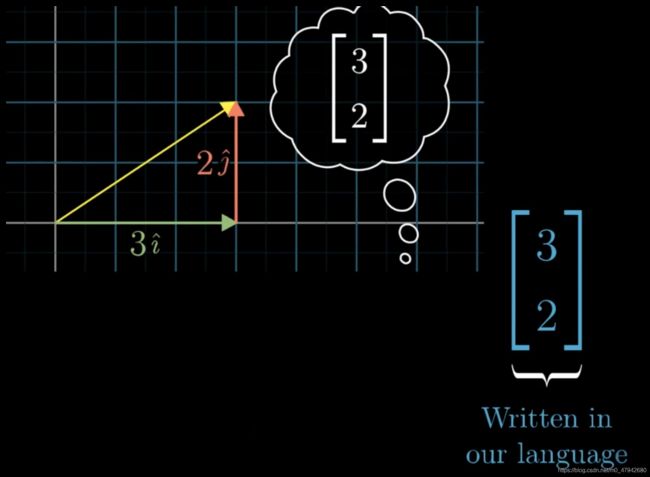
如果我们想用jen的语言来表示我们语言中的（3，2），我们该怎么做？

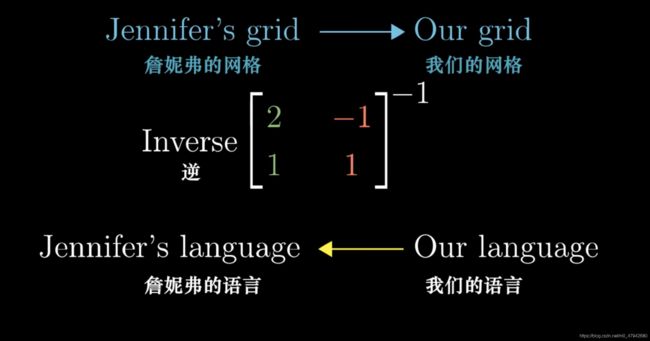
如果要把用我们的语言描述转化为用jen的语言来描述，我们就要求这个矩阵的逆。

也就是说，我们使用逆矩阵，把用我们的语言所表示的向量（蓝色）转化称为用jen语言描述的向量（粉色）。在这里我们使用矩阵乘法。

也就是上图所示。

我们知道如果要对一个矩阵做变换就要在左边乘以变换的矩阵，如上图，我们让最右边的矩阵xy写轴互换，就给它坐乘中间的矩阵。那么把这个变换用jen的语言描述就是给它左乘逆矩阵。
基变换-线性变换-基变换的逆

也就是说对于形如上图的表达式表示的就是一种“视角的变化”，矩阵M是一种线性变换，给它乘上两边的东西就是从新的角度去看这个线性变换。

特征向量与特征值

什么是特征向量呢？在线性变换时，空间中可能会存在一种向量，在变换之后它们的方向并没有改变，只有大小发生了变化。也就是说，这些特殊的向量在线性变换之后依旧留在它们张成的空间里，这样的向量就称为矩阵的特征向量，而特征值就是特征向量在变换中伸缩或者放大的比例因子。
也就是下图中的第一个方程。

通过数学分析我们就可以计算出
对于上图第三个方程，我们需要求出一个非0的特征向量，只有令左边的矩阵为0。而我们知道当且仅当矩阵所代表的变换将空间压缩到更低维度时，才会存在非0向量，使得矩阵和它的乘积为0，而空间压缩对应的矩阵行列式为0.因此我们可以用第四个方程求出特征值。我们再把特征值带入第三个方程就可以求出该向量了。

那么我们考虑一个问题：如果基向量全部都是特征向量会发生什么？根据简单的推算我们可以得出用特征向量作为基向量得到的线形变换矩阵是一个对角矩阵！矩阵的对角元就是该向量的特征值。

与课本相关内容的联系

学习笔记会在这里同步更新。