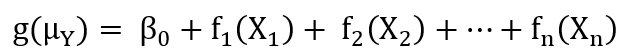r语言各形状编号_广义加性模型的简介、应用举例及R语言操作
广义加性模型的简介、应用举例及R语言操作
广义加性模型的定义
前文提到加性模型可描述为多元回归的非参数化平滑回归形式,并举例介绍了一般加性模型(general additive model)。在一般加性模型中,假定响应变量Y服从正态分布,自变量X和响应变量Y的条件均值之间的关系可简单表示为:
式中fn(X)是未指明的函数,需要非参数式地予以估计,“非参数”一词反映了函数fn(X)不是用参数来定义的。与参数多元回归(如多元线性回归)相比,加性模型放宽了对响应关系加和形式的限制,允许任意函数之和来建模结果,自变量和响应变量之间的关系可以为任意线性或非线性。
类似一般线性模型和广义线性模型(GLM)的关系,一般加性模型一般化为广义加性模型(GAM),代表了一类服务于一组来自指数分布族(如正态分布、指数分布、泊松分布、二项分布、负二项分布等)的响应变量的非参数化平滑回归框架,概括形式为:
此时fn(X)仍是非参数的函数,而响应变量Y服从指数分布族中的某种分布(不局限于正态性)。g(μY)代表了响应变量Y条件均值的函数(指数、泊松、二项、负二项等),又称连接函数,与在广义线性模型(GLM)中的理解相似,目的是将各类非正态的指数分布族响应变量的条件均值转化为正态形式的条件均值,以建立和自变量的非参数加和响应关系。
连接函数根据响应变量Y的实际分布而具体为不同公式。例如,当响应变量为泊松分布时,连接函数g(μY) = loge(Y)。一般加性模型事实上属于广义加性模型在正态响应变量时的特殊形式,此时g(μY) = Y。
接下来就展示在R语言中运行广义加性模型的一个例子,在过程中加深理解。
以一个泊松加性模型为例展示R语言执行广义加性模型
前文在“泊松回归的广义线性模型”中,展示了一个通过泊松回归分析计数型响应变量的例子,影响鱼类物种Rhinichthys cataractae丰度的环境因素。在前文中假设R. cataractae丰度的对数均值随环境是线性响应的,最终在6个给定的环境因素中挑选了3个对R. cataractae丰度有重要贡献的环境,并解释了它们的生物学意义。(广义线性模型中,除标准线性回归这种特殊形式外,所描述的均是响应变量通过某种转化形式得到近似正态的转化值后,拟合与自变量的线性关系,而非直接使用原始响应变量数值;如在泊松回归中,涉及了响应变量的某种形式的对数转化,因此泊松回归中自变量和响应变量的对数值之间存在线性关联)
对于其余3个被排除的环境因素而言,主要原因在于R. cataractae丰度的对数均值沿这些环境梯度的变化不存在明显的线性关系。可能归因于两种情况,一是数据比较离散和无序,R. cataractae丰度随这些环境值的改变而呈现无规律的状态,表明影响几乎是随机的;二是可能存在其它非线性的响应模式,R. cataractae丰度随这些环境值的改变虽然有规律但难以通过单向的递增或递减趋势描述出来,因而在广义线性模型的结果中不显著。如果是第一种情况,那就无需多加考虑;但若存在第二种情况,提示可能遗漏了对重要环境影响的解释。
因此,接下来尝试通过拟合泊松响应的广义加性模型(泊松加性模型)对这个数据进行探索,查看和比较这个数据集中,除了线性关系外,R. cataractae物种丰度和环境因素之间是否还存在其它可能的响应状态。
下文中所使用的示例数据和R代码的百度盘链接(提取码,fsls):
https://pan.baidu.com/s/1aAwZP_mQ3nWVk_EEfHnZyg
若百度盘失效,也可在GitHub的备份中获取:
https://github.com/lyao222lll/sheng-xin-xiao-bai-yu
示例数据概要
数据同样可在前文“泊松回归的广义线性模型”中获取。节选了马里兰州河流生物资源调查(https://dnr.maryland.gov/streams/Pages/mbss.aspx)的部分数据,一个生物学目的是探索可能影响鱼类物种丰度的环境因素,并对物种丰度变化的原因作出解释。
就节选的部分数据为例,记录了所调查的马里兰州河流中每75米长的区段水域内,鱼类物种Rhinichthys cataractae的丰度,并测量了每段水域中相应的环境特征。
其中第一列代表了调查河流区段的位置信息,其余各列依次为:
fish,水域中R. cataractae的个体数量,代表了物种丰度,一组计数型变量;
acre,水域流域面积(英亩,acre);
do2,水域溶解氧含量(毫克/升,mg/L);
depth,水域最大深度(厘米,cm);
no3,水域硝酸盐浓度(毫克/升,mg/L);
so4,水域硫酸盐浓度(毫克/升,mg/L);
temp,水域温度(摄氏度,℃)。
R包mgcv执行泊松加性模型
分析目的是确定影响R. cataractae丰度的环境成因,环境因素在分析中将作为自变量,R. cataractae丰度作为响应变量对待。R. cataractae丰度是一组计数型变量,在前文“泊松回归的广义线性模型”中,已经确定了R. cataractae丰度大致服从泊松分布,因此接下来考虑泊松加性模型进行探索式的分析。
在R中,可用于实现加性模型的R包很多,以下使用mgcv包中的方法执行广义加性模型。mgcv包中执行加性模型的函数是gam(),默认情况下其执行一般加性模型,可通过family参数指定响应变量类型更改为广义加性模型。
gam()拟合变量时,对于各自变量需要设置平滑器类型,以拟合响应变量和自变量的局部平滑。例如s()将平滑器指定为样条平滑,lo()将平滑器指定为LOESS平滑等,在下文示例中统一使用样条平滑来实现。其中有个关键问题,无论使用哪种平滑器,均需要谨慎设置合适的平滑参数值。平滑参数值的选择会强烈影响结果中曲线的平滑程度,甚至产生不同状态的变量响应趋势,进而导致不同的生物学意义理解和解读,详情可参考前文“一般加性模型”中的阐述。
在下文的示例中,没有对各变量设置特定的平滑参数,而是使用默认参数,让R自动评估。这种情况比较省事,但可能的问题在于机器选择方法难以贴合生物学实际,可能会产生存在矛盾解释的模型。实际情况中,您可能需要谨慎评估选择合适的平滑参数值,例如如果觉得拟合曲线形状显得很奇怪时,手动在s()中通过调试参数k后重新拟合回归,并借助相关的生物学背景知识辅助判断曲线的合理性。
#读取鱼类物种丰度和水体环境数据
dat <- read.delim('fish_data.txt', sep = 't', row.names = 1)
#使用 mgcv 包拟合广义加性模型
library(mgcv)
#详情 ?gam,这里通过 family='poisson' 指定泊松加性模型
#需要在 gam() 函数中指定自变量的局部平滑器类型,如 s() 的样条平滑、lo() 的 LOESS 平滑等
#以样条平滑 s() 为例,参数 k 可用于指定平滑程度,值越小约平滑,越高扭动越高,详情 ?s
#这里直接使用默认的平滑参数,只是可能有些不妥,作为示例请忽略这点
gam_poisson <- gam(fish~s(acre)+s(do2)+s(depth)+s(no3)+s(so4)+s(temp),
data = dat, family = 'poisson')
summary(gam_poisson)
#平滑回归曲线图,默认显示 95% 置信区间,通过 select 参数选择第 n 个自变量展示
par(mfrow = c(2, 3))
plot(gam_poisson, select = 1, pch = 20, shade = TRUE, residuals = TRUE)
plot(gam_poisson, select = 2, pch = 20, shade = TRUE, residuals = TRUE)
plot(gam_poisson, select = 3, pch = 20, shade = TRUE, residuals = TRUE)
plot(gam_poisson, select = 4, pch = 20, shade = TRUE, residuals = TRUE)
plot(gam_poisson, select = 5, pch = 20, shade = TRUE, residuals = TRUE)
plot(gam_poisson, select = 6, pch = 20, shade = TRUE, residuals = TRUE)
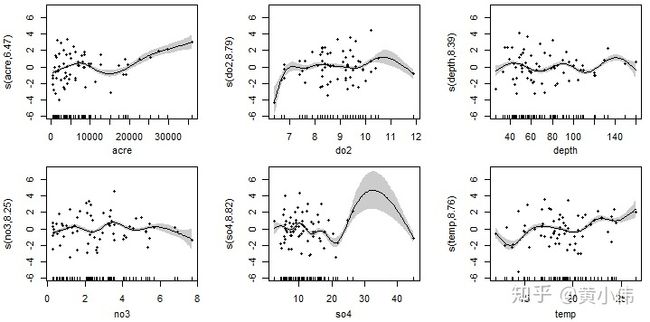
由于在加性模型中,变量间关系是非参数形式,通常无法通过简单的数学公式(如线性回归中简单的y=ax+b这种)来描述。因此,图形化的平滑曲线是常用在加性模型中观测变量间依赖性的方式,您可以通过曲线形状解释可能的生物学响应关系。但是与一般加性模型略有区别,广义加性模型的解释可能并不轻松,因为得出的模型是用连接函数的形式来表达的。例如对于这个泊松响应的计数型变量(R. cataractae丰度)而言,泊松加性模型的输出会把估计出的函数用对数形式来表达,图中纵轴其实反映了与R. cataractae丰度的对数均值有关的信息,而非原始R. cataractae丰度值,这种情况下需尝试从响应变量的对数水平角度上去理解。
例如在水域流域面积(acre)增加的梯度上,您可以将纵轴描述为R. cataractae丰度的对数随水域流域面积的增加而增加;但从曲线特征来看似乎是分段式的,15000英亩时存在一个拐点,可能水域面积此时突破了R. cataractae种群密度的限制。类似地理解,R. cataractae丰度的对数随水域溶解氧含量(do2)刚开始时升高,氧含量有助于鱼类生存;但随后在大范围区间内波动,表明后续水中溶氧量增加不再是R. cataractae种群数量的限制因素。在与水域硫酸盐浓度(so4)的关系中,R. cataractae丰度的对数在硫酸盐浓度20毫克/升前波动下降,暗示较高浓度的硫酸盐可能通过直接或其它间接方式对R. cataractae种群产生不利影响;硫酸盐浓度20毫克/升后的曲线非常奇怪,极有可能是so4≈45的那个离群点所致,提示需要在数据中删除它重新分析趋势。R. cataractae丰度的对数随水域温度(temp)出现波动增长,根据温度数值范围可知这些环境中没有极端值,整体上在一个温和的温度区间内,表明R. cataractae是一种喜温生物。
当然这只是根据曲线图的趋势,用眼睛观察后作出的解读,实际情况可能并非如此。正如上文提到的,如果更改曲线的平滑程度,曲线可能会呈现其它形状,从而产生其它的理解。例如这里更改水域溶解氧含量(do2)的平滑参数,您会发现响应关系和刚才的结果并不完全一致。
#更改平滑参数,将导致不同的生物学意义解释
#例如更改氧含量的平滑参数,在样条平滑 s() 中调试参数 k
gam_poisson1 <- gam(fish~s(acre)+s(do2, k = 3)+s(depth)+s(no3)+s(so4)+s(temp), data = dat, family = 'poisson')
gam_poisson2 <- gam(fish~s(acre)+s(do2, k = 5)+s(depth)+s(no3)+s(so4)+s(temp), data = dat, family = 'poisson')
par(mfrow = c(1, 3))
plot(gam_poisson, select = 2, pch = 20, shade = TRUE, residuals = TRUE)
plot(gam_poisson1, select = 2, pch = 20, shade = TRUE, residuals = TRUE)
plot(gam_poisson2, select = 2, pch = 20, shade = TRUE, residuals = TRUE)
在这个示例中更改水域溶解氧含量(do2)的平滑参数,左图是一开始自动确定平滑参数得到的回归曲线,中图是设置s()平滑参数k=3的结果,右图是设置s()平滑参数k=5的结果。在这些结果中,您可能产生对R. cataractae丰度的对数随水域溶解氧含量(do2)出现升高-波动、二次关系、升高-波动-降低的不同理解,进而导致对环境和物种关系产生完全不同的解释。
实际的生物学意义解读中,只允许一种正确的解释,因此解释不同参数的平滑回归输出时必须谨慎。拟合出的响应曲线必须结合实际情况判断,任何与当前研究对象的理解存在矛盾的地方都必须进行检查,否则很容易产生背离实际的曲解(白鱼同学就是一个写代码的,欠缺生物学背景,所以解答不了哪种响应更值得被选择)。
关于自变量的显著性及模型解释率
尽管加性模型作为非参数平滑回归的一种类型,常作为探索性工具来使用,但在R语言中仍提供了对自变量的显著性、方差解释率等进行统计的方法,可直接通过summary()查看。
以上文使用默认参数的输出结果为例,暂且忽略这些回归曲线本身是否具有生物学意义,这里仅仅查看数学上的统计显著性。
#检验自变量的显著性以及评估回归整体的方差解释率
summary(gam_poisson)
结果似乎显示这些环境变量对R. cataractae丰度的非线性影响均是显著的。回归模型对响应变量整体方差解释率高达90%(R2=0.891),表明这些环境变量能够在R. cataractae丰度的对数水平上解释90%的方差,拟合结果非常出色。
然而这些统计值可能意义并不大。各自变量的显著性受其在局部回归平滑器中设置的平滑参数的影响,并且不同的平滑参数也会强烈影响解释率。理论上,曲线越平滑趋于直线,R2越低,自变量的p值水平越高(越不显著);曲线扭动越曲折,R2越高,自变量的p值水平越低(越显著)。但如上文所提到的,曲线平滑程度的选择很具主观性,这是个值得考虑的问题,它直接影响生物学意义解读。因此不同于常规的参数回归(如线性模型、广义线性模型等),在广义加性模型这类非参数的平滑回归中,过分追求R2的优度并不是可取的行为(可能导致曲线过于波动,呈现无序状态,导致回归难以或无法被解释),应将探索感兴趣的、值得被解释的变量响应趋势放在重点。
* 偏大离差以及准泊松加性模型
正如在泊松回归中的问题一样,偏大离差也是泊松响应的广义加性模型的一个潜在问题。关于偏大离差的概念可参考前文“泊松回归的广义线性模型”,这里不再多说。解决方法也比较类似,拟合考虑了偏大离差问题的泊松加性模型时,通过指定gam()函数中参数family='quasipoisson'来实现,即准泊松加性模型。
#考虑了偏大离差问题的泊松加性模型
gam_quasipoisson <- gam(fish~s(acre)+s(do2)+s(depth)+s(no3)+s(so4)+s(temp),
data = dat, family = 'quasipoisson')
summary(gam_quasipoisson) #查看自变量的显著性
plot(gam_quasipoisson) #查看拟合曲线
回归曲线不再展示了,除family='quasipoisson'外其它gam()参数都相同的情况下,泊松加性模型和准泊松加性模型的拟合曲线是完全一致的,描述了同样的变量响应趋势。
二者不同之处在于summary()统计时对显著性的评估,准泊松加性模型提升了显著性的标准,把p值放大了,目的是减少偏大离差的影响。可以看到结果中,部分环境变量变得不那么显著。不过这种偏大离差问题更多在泊松回归中被考虑,而在非参数的泊松加性模型中似乎意义并不大,因为泊松加性模型更多是作为探索性方法使用。并且还如上文所提及的,平滑回归中p值本身的存在意义也应多加思考。
与参数模型(如广义线性模型)的比较
回顾前文“多元线性回归”或“泊松回归的广义线性模型”使用相同数据的分析结果,均显示acre(流域面积)、depth(水域深度)和no3(硝酸盐浓度)的增加有助于R. cataractae丰度的提升,同时其余3个变量与R. cataractae丰度或者丰度对数间没有显著的线性关系而不参与生物学解释。
但本文的泊松加性模型所得结果与它们存在很多不相似之处。一种可能是广义加性模型的非参数平滑方法描述出了线性模型无法体现的部分潜在非线性响应模式,如波动式的升高或降低等。然而这种波动也很大可能是数据不稳定、较高离散度或随机误差所致的,非参数平滑回归的曲线拟合强行将它们考虑在内,有可能对生物学响应意义的解释带来错误理解。特别还受限于对曲线平滑程度的选择,可能产生多个冲突的结果影响判断。相比之下参数回归方法一般将这种波动理解为随机的无规律的响应故排除在外,因而通常是更合适的做法,这也说明了这种非参数平滑通常不如线性回归等参数方法更具统计功效。
尽管如此,加性模型仍具有很高的应用价值。但大都作为探索性工具来使用,不做过多的批判性评价,作为辅助手段寻求可能的变量间响应关系,提出和检验关于模型的假设。当前这个示例里面的科学问题是用一个连续函数描述R. cataractae丰度与当前给定的环境变量之间的关系是否合理。如果期望是连续、光滑的关系,那么这个泊松响应的广义加性模型是合理的,否则就不那么合适。
文献中使用广义加性模型分析的实例
最后再简单提及3篇文献中使用广义加性模型分析生物学问题的案例,帮助加深对它使用的理解。
注意的是,由于一般加性模型(general additive model)也是广义加性模型(generalized additive model,GAM)的一种特殊形式,使得很多文献中不区分具体类型,统一概括为广义加性模型一词。因此,阅读涉及此类方法的文献时需要留意,如果作者没有明确提到所使用的广义加性模型的具体类型(例如泊松、负二项、二项响应等),不排除是正态响应的一般加性模型的可能。
文献一
登革热(dengue)是一种蚊媒疾病,尽管已经存在大量的统计和数学模型对气候-流行病的关联和爆发风险进行了评估,但很少将蚊子种群动态纳入统一的框架中。Li等(2019)使用中国部分地区2005-2015年的蚊子种群丰度监测数据,建立了当地气候与季节性登革热风险联系的预测模型。结果表明,气候因素通过影响局部媒介动态(蚊子种群丰度)的变化,驱动登革热的流行病学和传播周期。
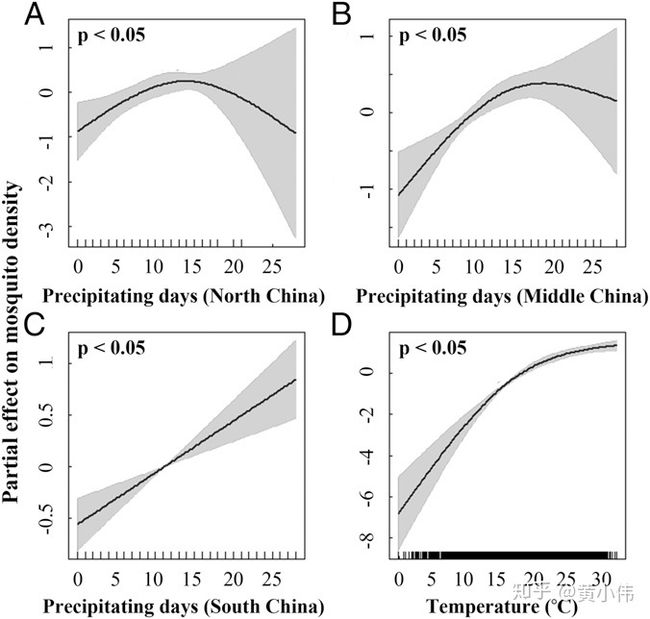
文中部分章节中,作者通过广义加性模型描述了蚊子种群丰度随气候环境因素的响应关系,发现蚊子密度与当地气候条件之间存在显著的关联。总体而言,蚊子密度随降水时间的增加而增加。中国北部和中部地区中的非线性响应趋势指示蚊子密度约在降水15 d/mo时达到最大。中国北部地区的气候整体偏干燥,降水天数较少,且大范围降水时间过于集中,可能导致在更长的降水时间中估计降水对蚊子密度的影响方面存在较大不确定性。中国南部地区降水丰富,气候温暖湿润,蚊子密度随降水时间近似线性增长关系。蚊子密度和温度之间同样存在显著的非线性响应,温暖气候有助于蚊子密度的提升,但更高温炎热时趋势逐渐平缓。
原文图2,探索温度和降水对蚊子种群密度的影响。使用广义加性模型量化了中国华北(A)、中部(B)、华南(C)降水日数以及月平均温度(D)对蚊子密度的潜在非线性影响,并显示了各气候预测变量对蚊子密度影响的显著性检验结果。
文献二
细胞代谢是高度动态的,植物细胞培养是剖析植物生物合成途径并研究哪些因素影响代谢的重要模型系统。Saw等(2017)通过代谢组学结合统计建模技术研究植物代谢,揭示了茉莉酸甲酯诱导的葡萄细胞培养物中花色苷生物合成的动态变化。
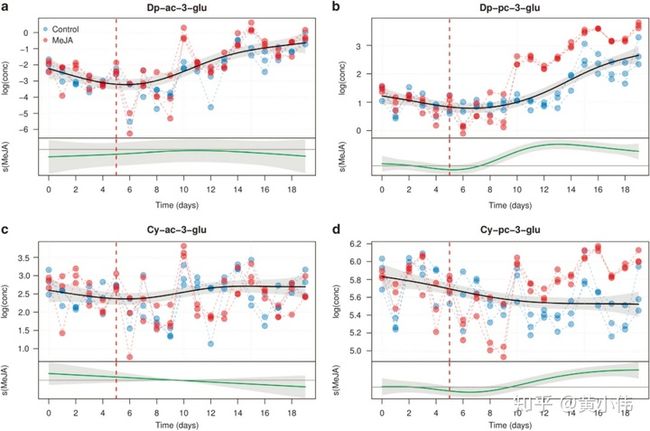
以下是文中的部分分析内容,作者通过广义加性模型的平滑拟合曲线展示了细胞培养物中花色苷浓度随处理和时间的变化趋势,显示茉莉酮酸甲酯显著调节了不同种类花色苷的生物合成。
原文图3,糖基化花色苷浓度-处理-时间关系的平滑曲线,MeJA表示茉莉酮酸甲酯的诱导。
原文图4,乙酰化花色苷浓度-处理-时间关系的平滑曲线,MeJA表示茉莉酮酸甲酯的诱导。
文献三
Tse等(2011)在一项对肺癌患者人群的调查研究中,评估了几种主要的肺癌病理学风险与患者戒烟时间的关系,以通过戒烟后肺癌风险的下降率以及早期下降幅度阐述戒烟的重要性。
文中部分章节中,作者通过广义加性模型探索人群中患者戒烟后的多年时间内肺癌的发病率,发现所有病理学亚型的肺癌风险都与患者戒烟状态密切相关。特别是在戒烟的前5年时间内,肺癌风险水平显著下降。随后的多年时间中,风险比率继续下降,但下降幅度趋渐趋平缓,接近非吸烟人群中的肺癌发生水平。该项研究向社会传达了一个积极的信息,对于吸烟者而言,戒烟后的短短5年时间即可有效降低肺癌发生的风险。
原文图1,广义加性模型描述了主要病理学亚型的肺癌风险与患者戒烟时间的关系。(A)所有肺癌、(B)肺腺癌、(C)肺鳞状细胞癌、(D)肺小细胞癌。
参考资料
钱松. 环境与生态统计:R语言的应用(曾思育译). 高等教育出版社, 2011.
Li R, Xu L, Bjornstad O N, et al. Climate-driven variation in mosquito density predicts the spatiotemporal dynamics of dengue. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116(9): 3624-3629.
Saw N M, Moser C, Martens S, et al. Applying generalized additive models to unravel dynamic changes in anthocyanin biosynthesis in methyl jasmonate elicited grapevine ( Vitis vinifera cv. Gamay) cell cultures. Horticulture research, 2017, 4(1): 1-7.
Tse L A, Yu I T, Qiu H, et al. Lung Cancer Decreased Sharply in First 5 Years After Smoking Cessation in Chinese Men. Journal of Thoracic Oncology, 2011, 6(10): 1670-1676.