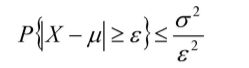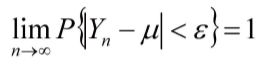机器学习(二)——数理统计与参数估计
概率论:
期望;方差;偏度;峰度;协方差;相关系数;独立相关性;
数理统计:
大数定理;切比雪夫不等式;矩估计;极大似然估计
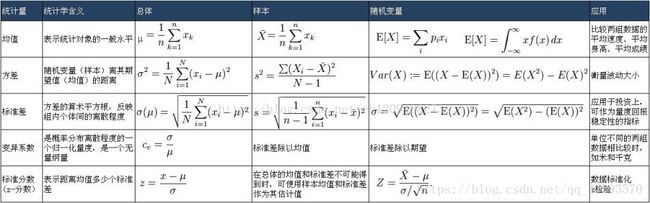
1、统计量概念
1.1 期望
从感情上来讲就是预期的值,数值意义上来讲可以认为是概率加权下的“平均值”。
特别地,若特征X和Y相互独立时,E(XY)=E(X)E(Y);反之不成立。如果已知E(XY)=E(X)E(Y),只能说明X和Y不相关。那么不相关和独立有什么区别呢?独立就是两者没有任何关系,当然也不相关。相关指的是线性关系,不相关指没有线性关系,但是呢可能有其他关系,不一定独立。所以独立一定不相关,不相关不一定独立。
1.2方差
度量随机变量及其数学期望之间的偏离程度。
公式定义上,方差是函数[X-E(X)]2的期望,因此,离散型、连续型随机变量的方差可统一表示为:
表示的是X的取值偏离期望值E(X)的程度。如果X和Y是独立的,那么Var(X+Y)=Var(X)+Var(Y)。方差的平方根是标准差。
总结一下,均值描述的是样本集合的中间点,它表达的信息是很有限的,而标准差描述的是样本集合的各个样本到中心点的距离的平均。比如两个集合:[1,9,13,21]和[9,10,12,13],两个集合的均值都是11,但是两个集合的差别还是很大的,后者比较集中,标准差更小一些,而前者的标准差就很大。所以标准差有效描述了集合的分散度。
1.3协方差
相关系数是用以反映变量之间相关关系密切程度的统计指标。
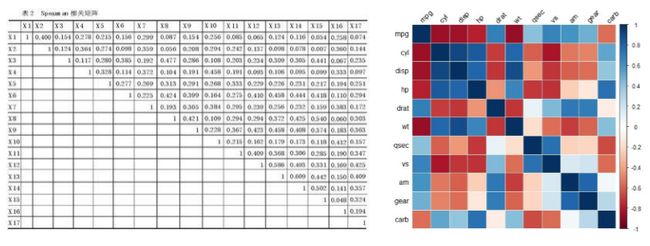
1.5协方差矩阵
![]()
协方差矩阵是对称阵。
1.6独立和不相关
独立比不相关性质更强。独立一定不相关,不相关不一定是独立。
2.1矩
X的k阶原点矩为![]()
X的k阶中心矩为![]()
总结:期望(一阶原点矩)
方差(标准差,二阶中心距)
变异系数
偏度(三阶)
峰度(四阶)
2.2 偏度
定义:偏度衡量随机变量概率分布的不对称性,是相对于平均值不对称程度的度量。
2.3峰度
直观看来,峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量,如果峰度大于三,峰的形状比较尖,比正态分布峰要陡峭。反之亦然
三. 重要定理与不等式
3.1切比雪夫不等式
切比雪夫表达的是随机变量X及其期望和方差之间的关系,表达式如下:
这个不等式说明,X的方差越小,事件发生的概率越大,X的取值基本上集中在期望附近。为统计推断中依据样本平均数估计总体平均数提供了理论依据。特别需要注意的是,切比雪夫定理并未要求Xi 同分布,相较于大数定律更具一般性。
3.2大数定理
大数定理比较有意思哈,是概率论历史上第一个极限定理,原为“伯努利定律”,后改为大数定理,是讨论随机变量序列的算术平均值向随机变量各数学期望的算术平均值收敛的定律。在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律。通俗地说,这个定理就是,在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。比如,我们向上抛一枚硬币,硬币落下后哪一面朝上本来是偶然的,但当我们上抛硬币的次数足够多后,达到上万次甚至几十万几百万次以后,我们就会发现,硬币每一面向上的次数约占总次数的二分之一,偶然中包含着某种必然。
大数定理的定义:设随机变量Xi相互独立,并且具有相同的期望和方差。作前n个随机变量的平均Yn,则对于任意正数ε,有公式
那么大数定理的存在,为我们的实际应用带来了哪些好处呢?很多时候,大数定理为“用频率来估计概率”提供了有力的理论依据。比如正态分布的参数估计,朴素贝叶斯做垃圾邮件分类,隐马尔科夫模型有监督参数学习等等。
3.3中心极限定理
中心极限定理指出了大量随机变量积累分布函数逐点收敛到正态分布的积累分布函数的条件。定义为:设随机变量X1、X2...Xn...相互独立,服从同一分布,并具有相同的期望和方差,则随机变量Yn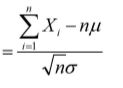 的分布收敛到标准正态分布。
的分布收敛到标准正态分布。
在实际问题中,很多随机现象可以看作许多因素的独立影响的综合反映,往往近似服从正态分布。比如城市耗电量——大量用户的耗电量总和。
四. 用样本估计参数
4.1矩估计
矩估计的原理总结来讲为:令总体矩的k阶矩分别等于样本的k阶矩即可,至于到底会涉及到k是多大就要看你要估计的总体中包含几个未知参数了,包含几个k就应该是几。
矩估计,即矩估计法,也称“矩法估计”,就是利用样本矩来估计总体中相应的参数。首先推导涉及感兴趣的参数的总体矩(即所考虑的随机变量的幂的期望值)的方程。然后取出一个样本并从这个样本估计总体矩。接着使用样本矩取代(未知的)总体矩,解出感兴趣的参数。从而得到那些参数的估计。
矩估计的理论依据就是基于大数定律的,大数定律语言化的表述为:当总体的k阶矩存在时,样本的k阶矩依概率收敛于总体的k阶矩,即当抽取的样本数量n充分大的时候,样本矩将约等于总体矩。
优点:在不清楚总体分布具体属于什么分布的情况下,只需要根据均值和方差进行估计即可。 缺点:如果在总体分布已知的情况下,并不能很好的使用对应分布类型的信息,因为矩估计根本就不看重总体分布到底属于那种类型。
4.2极大似然估计
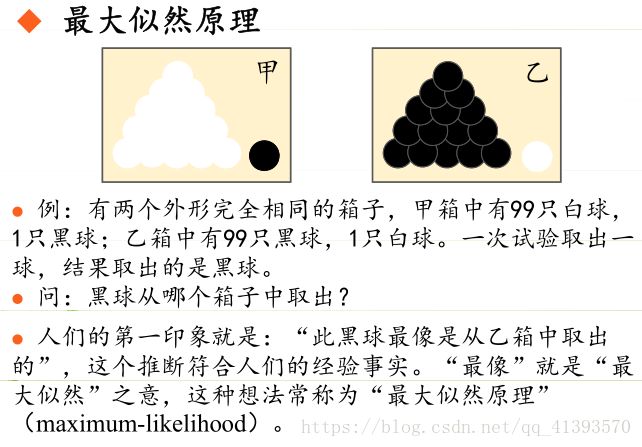
它是建立在极大似然原理的基础上的一个统计方法,极大似然原理的直观想法是,一个随机试验如有若干个可能的结果A,B,C,... ,若在一次试验中,结果A出现了,那么可以认为实验条件对A的出现有利,也即出现的概率P(A)较大。
求极大似然函数估计值的一般步骤:
参考:https://blog.csdn.net/zengxiantao1994/article/details/72787849