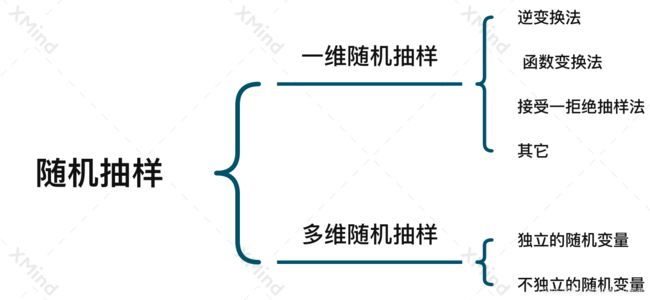
一般随机抽样
一般随机抽样
我们知道蒙特卡洛模拟在金融领域有着广泛的应用,比如说模拟股票的路径,通常来讲我们会假设股票价格服从以下的随机过程:
d S t = r S t d t + σ S t d W t (1) dS_t=rS_tdt+\sigma S_t dW_t\tag{1} dSt=rStdt+σStdWt(1)
如果我们把以上的随机过程离散化,就有如下的表达式
S t + 1 = S t + r S t Δ t + σ S t Δ W t (2) S_{t+1}=S_{t}+rS_t\Delta t+\sigma S_t\Delta W_t\tag{2} St+1=St+rStΔt+σStΔWt(2)
而 W t W_t Wt是一个布朗运动,因而 Δ W t \Delta W_t ΔWt可以表示成 Δ W t = Δ t ∗ N ( 0 , 1 ) \Delta W_t=\sqrt{\Delta t}*\mathcal{N}(0,1) ΔWt=Δt∗N(0,1)。蒙特卡洛模拟即是产生服从正态分布的随机数,从而可以模拟出服从(1)的资产过程,详见CIR过程蒙特卡洛模拟。
MATLAB中我们知道可以通过randn这个命令来产生服从正太分布的随机数,对于其它的分布形式,比如说Possion分布,Weibull分布,Binomial分布等等,我们也可以有现成的命令来产生相应的随机数。但是,如果我们要产生一些不常见分布的随机数,或者说如果大家好奇这些命令背后的过程,就需要说说随机数抽取的原理,我们这里所说的随机抽样即是已知分布形式时,如何产生相应的随机数。
逆变换法
逆变换法的原理在于如果我们能够求出已知分布 Y = F ( X ) Y=F(X) Y=F(X)的逆函数的解析形式,即 X = F − 1 ( Y ) X=F^{-1}(Y) X=F−1(Y), 我们即可以通过这个解析表达式来产生满足既定分布的随机数,这里需要注意的是, Y Y Y通常在0,1之间取值,所以我们假定它是一个0到1的均匀分布 U ( 0 , 1 ) U(0,1) U(0,1), 下面的几个例子可以帮助大家理解逆变换法的原理。
-
均匀分布(Uniform Distribution)
pdf: f ( x ) = { 1 b − a a ≤ x ≤ b 0 其它 f(x)=\left\{\begin{array}{cc} \frac{1}{b-a} & a \leq x \leq b \\ 0 & \text { 其它 } \end{array}\right. f(x)={ b−a10a≤x≤b 其它
cdf: F ( x ) = x − a b − a , a ≤ x ≤ b F(x)=\frac{x-a}{b-a}, a \leq x \leq b F(x)=b−ax−a,a≤x≤b
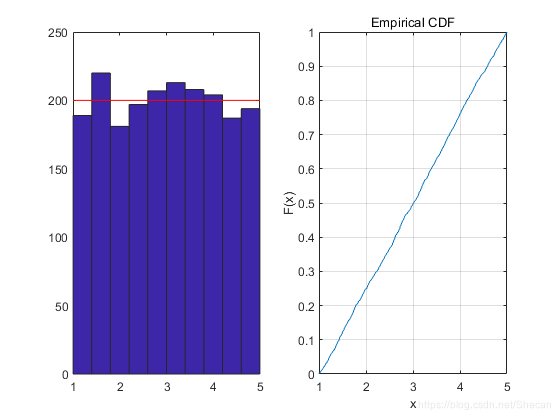
Inverse Random: x = ( b − a ) y + a x=(b-a) y+a x=(b−a)y+aMatlab 代码
u1=rand(1,2000); a=1; b=5; x1(1:2000)=0; for i=1:2000 x1(i)=a+(b-a)*u1(i); end hist(x1,10) hold on t=linspace(1,5,100); y=ones(length(t),1).*1/(b-a); scale=2000*4/10; plot(t,scale*y,'r') hold off
-
指数分布指数分布(exponential distribution)
pdf: f ( x ) = { λ e − i x x > 0 0 其它 f(x)=\left\{\begin{array}{cc} \lambda e^{-i x} & x>0 \\ 0 & \text { 其它 } \end{array}\right. f(x)={ λe−ix0x>0 其它
cdf: F ( x ) = 1 − e − λ x , x > 0 F\left(x\right)=1-e^{-\lambda x}, x>0 F(x)=1−e−λx,x>0
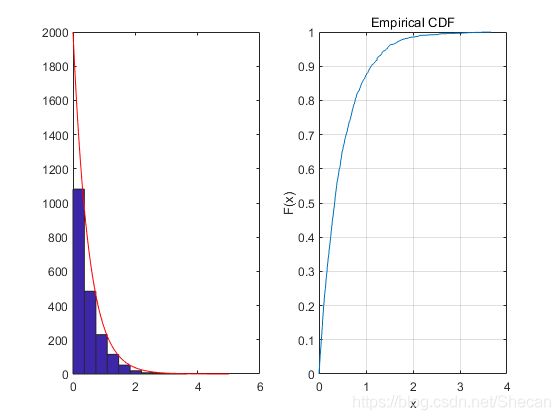
Inverse Random: x = − 1 λ ln ( 1 − y ) x=-\frac{1}{\lambda }\ln \left(1-y\right) x=−λ1ln(1−y)Matlab 代码:
u2=rand(1,2000); v=2; X2(1:2000)=0; for i=1:2000 X2(i)=-log(u2(i))/v; end subplot(1,2,1) hist(X2,10) hold on t=linspace(0,5,100); y=exp(-v*t).*v; scale=2000*5/10; plot(t,scale*y,'r') hold off subplot(1,2,2) cdfplot(X2)
函数变换法
有些分布的逆函数比较难求,比如说正态分布,这个时候我们可以通过变量替换的方法来得到解析表达式。
通过Box-Muller变换(直角坐标和极坐标的转换),我们可以有如下的表达式:
x 1 = ( − 2 ln r 1 ) 1 / 2 cos ( 2 π r 2 ) x 2 = ( − 2 ln r 1 ) 1 / 2 sin ( 2 π r 2 ) r 1 , r 2 ∼ U ( 0 , 1 ) \begin{array}{c} x_{1}=\left(-2 \ln r_{1}\right)^{1 / 2} \cos \left(2 \pi r_{2}\right) \\ x_{2}=\left(-2 \ln r_{1}\right)^{1 / 2} \sin \left(2 \pi r_{2}\right) \\ r_{1}, r_{2} \sim U(0,1) \end{array} x1=(−2lnr1)1/2cos(2πr2)x2=(−2lnr1)1/2sin(2πr2)r1,r2∼U(0,1)
详细推导过程见Box-Muller。
Matlab 代码:
mm=10000;
R1=unifrnd(0,1,mm,1);
R2=unifrnd(0,1,mm,1);
X = sqrt(-2*log(R1)).*cos(2*pi.*R2);
% 可视化
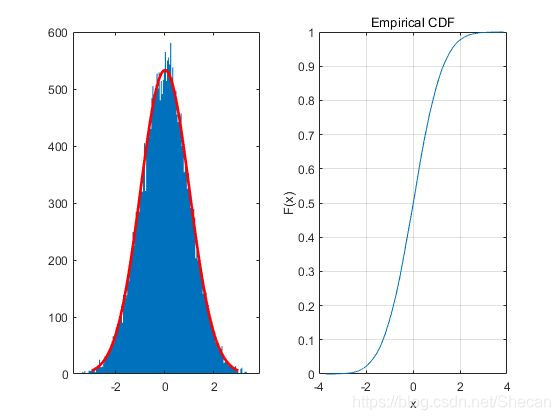
subplot(1,2,1),cdfplot(X)
subplot(1,2,2),histfit(X)
可以通过k-s检验和qqplot的方法来检验它的正态性:
h=kstest(X, [X normcdf(X, 0,1)])%h=0, kstest fails to reject the null hypothesis at the default 5% significance level, suggesting it is normal distribution.
figure
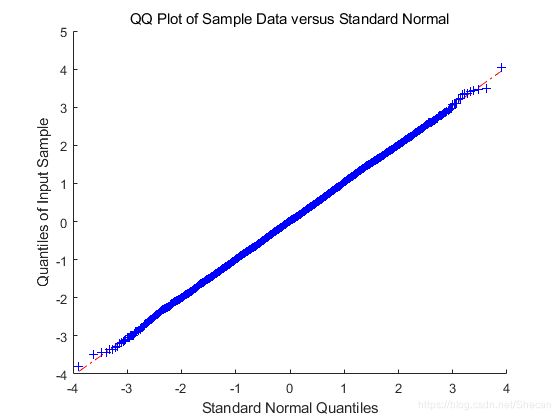
qqplot(X)
comments: The plot produces an approximately straight line, suggesting that X follow a normal distribution.
拒绝-接受法
对于有些分布,我们无法求解出逆函数的解析表达式,拒绝-接受法给我们提供了一般抽样的另一种思路。
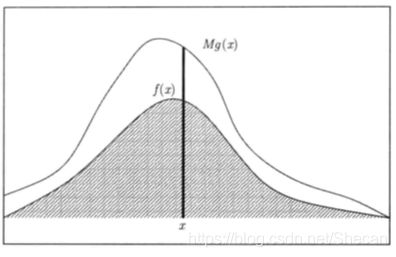
直观解释就是我们假设另外一个已知的简单分布 g ( x ) g(x) g(x), 使得 M g ( x ) Mg(x) Mg(x)可以完全覆盖所需的分布 f ( x ) f(x) f(x)。选取满足分布 g ( x ) g(x) g(x)中的点,如果点落到 f ( x ) f(x) f(x)中就接受它,否则就拒绝它。当然,这种解释是不严谨的,更加严谨的数学解释可以通过证明以下的概率公式来理解:
P ( X < x ) = P ( y < x ∣ u ≤ f ( y ) M g ( y ) ) P(X
即右边的这个条件分布等同于我们所需的分布,因而我们可以用这个关系来进行随机抽样。详细的推导可以参见《随机模拟方法与应用》第五章,依然以正态分布为例:
N = 100000;
M = 1/(sqrt(2*pi));
Y = unifrnd(-4,4,1,N);
U = unifrnd(0,1,1,N);
gy = 1;
fy = (1/(sqrt(2*pi)))*exp(-Y.^2./2);
X = Y(U同理,我们也可以用kstest和qqplot更为严谨地去检查它的正态性。
多维随机抽样
各个维度随机变量相互独立
各个维度随机变量不独立(Cholesky Decomposition正交分解)
如果我们要抽样出一个高维的随机分布,通常说我们要对其每个维度进行随机抽样,如果每个维度的变量之间是相互独立的,那么非常容易,我们只要对每个维度进行抽样,然后扩展到多维即可,依然以正态分布为例:
Matlab代码:
N=1000;
X=randn(N,2);
subplot(1,2,1),plot(X(:,1),X(:,2),'k.')
subplot(1,2,2),hist3(X,[10,10])
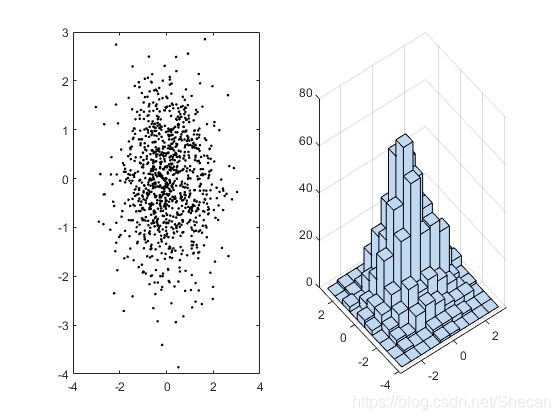
可以画出二维独立正态分布的直方图和散点图:
如果各个维度之间的分布不独立,具有一定的相关性,那我们又该如何抽样出具有相关性的高维随机变量呢,这个时候大家需要知道一个概念叫做Cholesky正交分解。
Cholesky Decomposition正交分解
目标:构造一个新的向量 Y = L − 1 X Y=L^{-1} X Y=L−1X,使得
cov ( Y , Y T ) = L − 1 E ( X X T ) ( L − 1 ) T = L − 1 Σ ( L − 1 ) T = Σ Σ − 1 = I \textrm{cov}\left(Y,Y^T \right)=L^{-1} E\left(XX^T \right){\left(L^{-1} \right)}^T =L^{-1} \Sigma {\left(L^{-1} \right)}^T =\Sigma \Sigma^{-1} =I cov(Y,YT)=L−1E(XXT)(L−1)T=L−1Σ(L−1)T=ΣΣ−1=I
其中 Σ \Sigma Σ是协方差矩阵,I 是单位矩阵,L是一个下三角矩阵并满足 L L T = Σ LL^T =\Sigma LLT=Σ。
反之,我们就可以通过独立向量 Y Y Y, 反推出具有相关关系的 X X X。
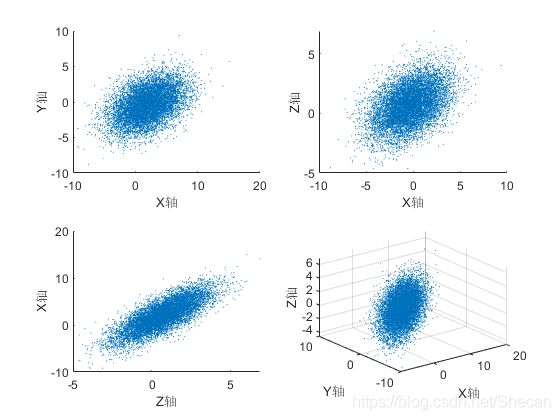
例如,生成一个三维的多元正态分布 X = ( X 1 , X 2 , X 3 ) X=\left(X_1 ,X_2 ,X_3 \right) X=(X1,X2,X3),其中, X 1 ∼ N ( 2 , 3 ) X_1 \sim N\left(2,3\right) X1∼N(2,3), X 2 ∼ N ( − 1 , 2 ) X_2 \sim N\left(-1,2\right) X2∼N(−1,2), X 3 ∼ N ( 0 , 1 ) X_3 \sim N\left(0,1\right) X3∼N(0,1)并满足如下的协方差矩阵
Σ = [ 1 0 . 3 0 . 4 0 . 3 1 0 . 2 0 . 4 0 . 2 1 ] \Sigma =\left\lbrack \begin{array}{ccc} 1 & 0\ldotp 3 & 0\ldotp 4\\ 0\ldotp 3 & 1 & 0\ldotp 2\\ 0\ldotp 4 & 0\ldotp 2 & 1 \end{array}\right\rbrack Σ=⎣⎡10.30.40.310.20.40.21⎦⎤
Matlab代码:
N = 10000;
% 生成独立的随机变量
Y = [normrnd(2,3,1,N);normrnd(-1,2,1,N);normrnd(0,1,1,N)];
rho = [1,0.3,0.4;0.3,1,0.2;0.4,0.2,1];
L = chol(rho,'lower');
% 构造一个协方差矩阵为Σ的随机变量
X = L*Y;
figure(3)
subplot(2,2,1)
scatter(X(1,:),X(2,:),'marker','.','sizedata',1)
xlabel('X轴');ylabel('Y轴')
subplot(2,2,2)
scatter(X(2,:),X(3,:),'marker','.','sizedata',1)
xlabel('X轴');ylabel('Z轴')
subplot(2,2,3)
scatter(X(3,:),X(1,:),'marker','.','sizedata',1)
xlabel('Z轴');ylabel('X轴')
subplot(2,2,4)
scatter3(X(1,:),X(2,:),X(3,:),'marker','.','sizedata',1)
xlabel('X轴');ylabel('Y轴');zlabel('Z轴');
Reference
肖柳青, 周石鹏. 随机模拟方法与应用[M]. 北京大学出版社, 2014.
Huynh. Stochastic Simulation and Applications in Finance with Matla[M]// Stochastic simulation and applications in finance with MATLAB programs.