PyTorch深度学习（四）：神经网络（上）——理论推导

PyTorch深度学习（四）：神经网络（上）——理论推导

---

一、感知机(Perceptron)

1.感知机概述

感知机是一个二分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取 $+1$（正类）、$-1$（负类）

设输入空间（特征空间）为 $\mathbf{x}=\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]\subseteq R^n$， 输出空间为 $y=\{+1,-1\}$，输入 ${\mathbf{x}}^{(i)}$ 表示实例的特征向量，对应于输入空间（特征空间）$\mathbf{x}$ 的点，输出 $y^{(i)}\in y$ 表示实例的类别，则由输入空间到输出空间有如下映射：
$$f(x)=sign(⟨\mathbf{w},\mathbf{x}⟩+b)$$

其中 $f(x)=sign(x)$ 为符号函数，表示如下：
$$sign(x)=\{\begin{array}{ll}1,& x>0\\ 0,& x=0\\ -1,& x<0\end{array}$$

它利用了上一章所讲的线性回归为基础，因此，感知机模型可以用线性方程来做几何解释：

感知机是一种线性分类模型，它分为两部分：线性部分、激活函数。如图所示，它可以根据输入空间（特征空间）的线性回归值：$⟨\mathbf{w},\mathbf{x}⟩+b$，其中，$\mathbf{w}$ 为线性方程的权重，$\mathbf{x}$ 为输入空间（特征空间），$b$ 为偏差，得到线性回归值 $⟨\mathbf{w},\mathbf{x}⟩+b$ 后，再将该线性回归值输入到 $f(x)=sign(x)$ 的激活函数中，即可得到分类结果 $y=\text{Output}$，感知机将最终结果分为两类，如下：
$$y=\{\begin{array}{ll}正类(+1)& ,o_1=⟨\mathbf{w},\mathbf{x}⟩+b>0\\ 负类(-1)& ,o_1=⟨\mathbf{w},\mathbf{x}⟩+b<0\\ 0& ,o_1=⟨\mathbf{w},\mathbf{x}⟩+b=0\end{array}$$

注意，传统的感知机使用的激活函数是 $sign(x)$，这里先提一下：感知机激活函数必须是非线性的，后面再分析原因

若用几何来解释，则在空间中，空间被一超平面 $⟨\mathbf{w},\mathbf{x}⟩+b$ 划分为两个空间，当样本点位于该超平面的上方，即 $⟨\mathbf{w},\mathbf{x}⟩+b>0$ 时，则被分为正类；当样本点位于该超平面的下方，即 $⟨\mathbf{w},\mathbf{x}⟩+b<0$ 时，则被分为负类，以猫狗分类为例，如图：

当然，非线性函数（激活函数） 除了符号函数 $sign(x)$ 外，还可以使用其他函数，如：阶跃函数 $u(x)$，当 $x>0$ 时分为正类 $+1$，当 $x<0$ 时分为负类 $0$

2.感知机学习策略

假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练集正实例点和负实例点分开的超平面 $S$：$⟨\mathbf{w},\mathbf{x}⟩+b$

为了找出这样的超平面，需要定义一个损失函数并将损失函数极小化，感知机采用了：误分类点到超平面 $S$ 的总距离作为损失函数，为此，我们先写出输入空间 $R^n$ 中任一点 ${\mathbf{x}}_0$ 到超平面的距离：
$$d=\frac{\mid ⟨\mathbf{w},{\mathbf{x}}_0⟩+b\mid }{||\mathbf{w}||}，其中||\mathbf{w}||=\sqrt{(\sum _i{w}_i{)}^2}$$

这里 $||\mathbf{w}||$ 是 $\mathbf{w}$ 的 $L_2$ 范数，但是距离 $d$ 的公式中包含绝对值，不易求导，需要进行处理

对于误分类的数据 $(x^{(i)},y^{(i)})$ 来说，这些数据满足：
$$y^{(i)}(⟨\mathbf{w},{\mathbf{x}}^{(i)}⟩+b)<0$$

因为真实类 $y^{(i)}$ 和预测类 $⟨\mathbf{w},{\mathbf{x}}^{(i)}⟩+b$ 的正负相反了，因此它们相乘为负

因此，误分类点 $x^{(i)}$ 到超平面 $S$ 的距离是：
$$d=-\frac{y^{(i)}(⟨\mathbf{w},{\mathbf{x}}^{(i)}⟩+b)}{||\mathbf{w}||}$$

这样就可以把原公式中的绝对值去掉了，假设超平面 $S$ 的误分类点集合为 $M$，那么所有误分类点到超平面的距离总和为：
$$-\frac{1}{||\mathbf{w}||}\sum _{x^{(i)}\in M}{y}^{(i)}(⟨\mathbf{w},{\mathbf{x}}^{(i)}⟩+b)$$

由于 $\frac{1}{||\mathbf{w}||}$ 是常数，因此不用考虑 $\frac{1}{||\mathbf{w}||}$，于是可以得到感知机学习的损失函数：

设数据集 $T=\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})\}$，其中 $x^{(i)}\in R^n$，$y^{(i)}\in \{+1,-1\}$，$M$ 为误分类点集合，则感知机 $sign(⟨\mathbf{w},\mathbf{x}⟩+b)$ 学习的损失函数定义为：
$$L(\mathbf{w},b)=-\sum _{x^{(i)}\in M}{y}^{(i)}(⟨\mathbf{w},{\mathbf{x}}^{(i)}⟩+b)$$

显然，损失函数是非负的，如果没有误分类点，损失函数值为 $0$，而且，误分类点越少，误分类点离超平面 $S$ 的总距离越近，损失函数值就越小，且该损失函数是连续可导的

3.感知机学习算法

在得到感知机的损失函数后，就需要通过算法来找到损失函数的极小值，由于损失函数是连续可导的，因此我们仍然使用梯度下降法，在使用梯度下降法之前，需要任意选取一超平面 ${\mathbf{w}}_0,b_0$ 作为初始值

假定误分类点集合 $M$ 是固定的，那么损失函数 $L(\mathbf{w},b)$ 的梯度由下式给出：
$${\nabla }_{\mathbf{w}}L(\mathbf{w},b)=-\sum _{x^{(i)}\in M}{y}^{(i)}{x}^{(i)}$$

$${\nabla }_{b}L(\mathbf{w},b)=-\sum _{x^{(i)}\in M}{y}^{(i)}，\because x_0=1$$

感知机使用随机梯度下降来更新权重，设选择误分类点 $(x^{(i)},y^{(i)})$ 来对 $\mathbf{w},b$ 进行更新，则：
$$w_i⟸w_i+\eta y^{(i)}{x}^{(i)}$$

$$b⟸b+\eta y^{(i)}$$

式中，$\eta (0<\eta \le 1)$ 是步长，即学习率，这样，通过小批量梯度下降，可以使 $L(\mathbf{w},b)$ 不断减小，直到收敛，当然，上述的过程都是在数据集线性可分的假设上进行的，若数据集线性不可分，则 $L(\mathbf{w},b)$ 不能收敛，可以通过指定训练次数或指定满意的 $L(\mathbf{w},b)$ 值作为训练结束标志

注意，上述过程是在误分类样本上进行的

4.感知机的收敛定理（Novikoff定理）

设训练数据集 $T=\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})\}$ 是线性可分的，其中 $x^{(i)}\in R^n$，$y^{(i)}\in \{+1,-1\}$，则：

（1）存在满足条件 $||{\hat{\mathbf{w}}}_{opt}||=1$ 的超平面 ${\hat{\mathbf{w}}}_{opt}\cdot \hat{\mathbf{x}}={\mathbf{w}}_{opt}\cdot \mathbf{x}+b$ 将训练数据集完全正确分开；且存在 $\gamma >0$，对所有 $i=1,2,...,N$：
$$y^{(i)}({\hat{\mathbf{w}}}_{opt}\cdot \hat{\mathbf{x}})=y^{(i)}({\mathbf{w}}_{opt}\cdot \mathbf{x}+b_{opt})\ge \gamma$$

（2）令 $R=\underset{1<i<N}{\max }||{\hat{x}}_i||$，则感知机在训练数据集上的误分类次数 $k$ 满足不等式：
$$k\le {\left(\frac{R}{\gamma }\right)}^2$$

证明：

（1） 因为训练数据是线性可分的，因此存在超平面可使得数据完全分开，记该超平面为：
$$S_{opt}:{\mathbf{w}}_{opt}\cdot \mathbf{x}+b_{opt}=0$$

把 $b$ 设为 $w_0$，则 $\hat{\mathbf{w}}=(w_0,w_1,w_2,...,w_n)$，把 $x_0=1$ 引入 $\mathbf{x}$ 中，记为 $\hat{\mathbf{x}}$，则：
$$\hat{\mathbf{w}}\cdot \hat{\mathbf{x}}=⟨\mathbf{w},\mathbf{x}⟩+b=\mathbf{w}\cdot \mathbf{x}+b$$

因为是线性方程，因此设 $||{\hat{\mathbf{w}}}_{opt}||=1$ 并不失一般性， 则：
$${\hat{\mathbf{w}}}_{opt}\cdot \hat{\mathbf{x}}={\mathbf{w}}_{opt}\cdot \mathbf{x}+b_{opt}=0，||{\hat{\mathbf{w}}}_{opt}||=1$$

对于 $i=1,2,...,N$，样本均被正确分类，有：
$$y^{(i)}({\hat{\mathbf{w}}}_{opt}\cdot {\hat{\mathbf{x}}}^{(i)})=y^{(i)}({\mathbf{w}}_{opt}\cdot {\mathbf{x}}^{(i)}+b_{opt})>0$$

$$令min[y^{(i)}({\hat{\mathbf{w}}}_{opt}\cdot {\hat{\mathbf{x}}}^{(i)})]=\gamma >0$$

$$则：y^{(i)}({\hat{\mathbf{w}}}_{opt}\cdot {\hat{\mathbf{x}}}^{(i)})=y^{(i)}({\mathbf{w}}_{opt}\cdot \mathbf{x}+b_{opt})\ge \gamma$$

定理（1）表明，被正确分类的样本点与超平面 $S$ 之间是存在一定的距离 $\gamma$ 的

（2） 设感知机算法从 ${\hat{\mathbf{w}}}_0=0$ 开始，如果实例被误分类，则更新权重，令 ${\hat{\mathbf{w}}}_{k-1}$ 是第 $k$ 个误分类实例之前的权重，即：
$${\hat{\mathbf{w}}}_{k-1}=({\mathbf{w}}_{k-1}^T,b_{k-1}{)}^T$$

则第 $k$ 个误分类实例应满足条件：
$$y_i⟨{\hat{\mathbf{w}}}_{k-1},{\hat{\mathbf{x}}}_i⟩=y_i({\mathbf{w}}_{k-1}\cdot {\mathbf{x}}_i+b_{k-1})\le 0$$

若 $(x^{(i)},y^{(i)})$ 是被 ${\hat{\mathbf{w}}}_{k-1}=({\mathbf{w}}_{k-1}^T,b_{k-1}{)}^T$ 误分类的数据（第 $k$ 个误分类实例），则 $\mathbf{w}$ 和 $b$ 的更新是：
$${\mathbf{w}}_k⟸{\mathbf{w}}_{k-1}+\eta y^{(i)}{\mathbf{x}}^{(i)}$$

$$b_k⟸b_{k-1}+\eta y^{(i)}$$

即
$${\hat{\mathbf{w}}}_k⟸{\hat{\mathbf{w}}}_{k-1}+\eta y^{(i)}{\hat{\mathbf{x}}}^{(i)}$$

在证明定理（2）前，先证明两个不等式：
$${\hat{\mathbf{w}}}_k\cdot {\hat{\mathbf{w}}}_{opt}\ge k\eta y\text{\hspace{1em}(4.1)}$$

$$||{\hat{\mathbf{w}}}_k|{|}^2\le k{\eta }^2{R}^2\text{\hspace{1em}(4.2)}$$

证明不等式 (4.1)：
$$\begin{array}{rl}{\hat{\mathbf{w}}}_k\cdot {\hat{\mathbf{w}}}_{opt}& =({\hat{\mathbf{w}}}_{k-1}+\eta y^{(i)}{\hat{x}}^{(i)})\cdot {\hat{\mathbf{w}}}_{opt}\\ & ={\hat{\mathbf{w}}}_{k-1}\cdot {\hat{\mathbf{w}}}_{opt}+\eta y^{(i)}{\hat{\mathbf{x}}}^{(i)}\cdot {\hat{\mathbf{w}}}_{opt}\\ & \ge {\hat{\mathbf{w}}}_{k-1}\cdot {\hat{\mathbf{w}}}_{opt}+\eta \gamma \end{array}$$

最后一步是根据定理（1）得到的，由此递推不等式，得：
$$\begin{array}{rl}{\hat{\mathbf{w}}}_k\cdot {\hat{\mathbf{w}}}_{opt}& \ge {\hat{\mathbf{w}}}_{k-1}\cdot {\hat{\mathbf{w}}}_{opt}+\eta \gamma \\ & \ge {\hat{\mathbf{w}}}_{k-2}\cdot {\hat{\mathbf{w}}}_{opt}+2\eta \gamma \\ & \ge ...\\ & \ge k\eta \gamma \end{array}$$

证明不等式 (4.2)：
$$\begin{array}{rl}||{\hat{\mathbf{w}}}_k|{|}^2& =||{\hat{\mathbf{w}}}_{k-1}+\eta y^{(i)}{\hat{\mathbf{x}}}^{(i)}|{|}^2\\ & =||{\hat{\mathbf{w}}}_{k-1}|{|}^2+2\eta y^{(i)}{\hat{\mathbf{w}}}_{k-1}\cdot {\hat{\mathbf{x}}}^{(i)}+{\eta }^2(y^{(i)}{)}^2||{\hat{\mathbf{x}}}^{(i)}|{|}^2\\ & =||{\hat{\mathbf{w}}}_{k-1}|{|}^2+2\eta y^{(i)}{\hat{\mathbf{w}}}_{k-1}\cdot {\hat{\mathbf{x}}}^{(i)}+{\eta }^2||{\hat{\mathbf{x}}}^{(i)}|{|}^2\\ & \le ||{\hat{\mathbf{w}}}_{k-1}|{|}^2+{\eta }^2||{\hat{\mathbf{x}}}^{(i)}|{|}^2\le ||{\hat{\mathbf{w}}}_{k-1}|{|}^2+{\eta }^2{R}^2\\ & \le ||{\hat{\mathbf{w}}}_{k-2}|{|}^2+2{\eta }^2{R}^2\le ...\le k{\eta }^2{R}^2\end{array}$$

综上所述，根据不等式 (4.1) 和 (4.2) 和 施瓦兹不等式，有：
$$k\eta \gamma \le {\hat{\mathbf{w}}}_k\cdot {\hat{\mathbf{w}}}_{opt}\le ||{\hat{\mathbf{w}}}_k||||{\hat{\mathbf{w}}}_{opt}||=||{\hat{\mathbf{w}}}_k||\le \sqrt{k}\eta R$$

$$k^2{\gamma }^2\le k{R}^2$$

于是
$$k\le {\left(\frac{R}{\gamma }\right)}^2$$

定理（2）表明，误分类的次数 $k$ 是有上界的，经过有限次搜索可以找到将训练数据完全正确分开的超平面 $S$

---

二、神经网络(Neural Network)、多层感知机(Multilayer Perceptron-MLP)

感知机可以解决二分类问题，然而，它只能对线性可分的训练集进行分类，不能解决异或(XOR)问题，如图所示：

作一条直线 $f(\mathbf{x})=⟨\mathbf{w},\mathbf{x}+b⟩$，无论直线如何摆放都无法解决异或(XOR)问题，这使得深度学习的发展进入了几十年的寒冬…

1.由XOR问题引出MLP和NN

虽然一条直线无法解决数据非线性可分的问题——感知机，但使用多条直线是可以解决样本非线性可分时的分类问题的——多层感知机，如图：

如上图所示，我们可以先通过蓝色的直线，将 $①③$ 分为正类 “$+$”，将 $②④$ 分为负类 “$-$”；再通过橘色的直线，将 $①②$ 分为正类 “$+$”，将 $③④$ 分为负类 “$-$”

经过 “蓝色直线” 和 “橘色直线” 的分类以后，再将他们各自的结果进行合并（相乘），最终可以得到正确的分类

这个时候，感知机已经由单层变为了多层感知机，其中 “蓝色直线” 和 “橘色直线” 所代表的分类过程分别是中间层的两个节点，也称为感知机的隐藏层

我们可以继续增加多个输入层、隐藏层、输出层的节点，就可以构成复杂的多层感知机，如图：

• 为了增加 多层感知机(MLP) 模型的表达能力，它可以包含更多个隐藏层，一个隐藏层又可以包含多个节点
• 从一层隐藏层的每个节点来看，都是一个线性模型加上一个激活函数，如：$sign(x)$
• 除了每一层的 $\mathbf{w}$ 和 $b$ 外，隐藏层节点个数和隐藏层的个数也成为超参数
• 一般来说，随着网络层数的逐渐加深，隐藏层各层的节点个数会越来越少，因为假设数据比较复杂，那么输入向量是很高维的，而输出是相对较少的（二分类，多分类），因此输入特征向量在经过隐藏层后后会逐渐压缩
• 各输出节点的输出值可以代表输入样本属于某一类别的可能性，即某一节点输出值越大，则该输入样本就越有可能属于这一类别，可能需要 One-Hot Encoding，即输出是一个由元素 $\{0,1\}$ 组成的向量

多层感知机构成了神经网络，实际上，多层感知机(MLP)就是我们通常所说的神经网络(NN)

2.神经网络的预测——前向传播(Forward Propagation)

前向传播是指输入特征向量 $\mathbf{x}=[x_1,x_2,...,x_n{]}^T$ 从神经网络的第一层逐渐从高层传递，最终得到一个或多个输出的过程

以三层神经网络为例，输入特征向量 $\mathbf{x}=[x_1,x_2,x_3{]}^T\in R^3$，输出数据是二维的。为方便描述，规定从第 $l-1$ 层的第 $k$ 个神经元到第 $l$ 层的第 $j$ 个神经元的权重为 $w_{jk}^{(l)}$，第 $l$ 层的第 $j$ 个神经元对应的偏差定义为 $b_j^{(l)}$，第 $l$ 层第 $j$ 个神经元的激活值（输出值）为 $a_j^{(l)}$，假设激活函数为 $\sigma (z)$，如图所示：

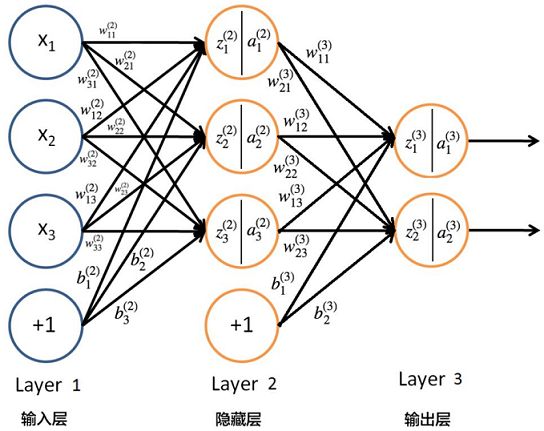
则对于第二层，它的输入是特征向量 $\mathbf{x}=[x_1,x_2,x_3{]}^T$，它的输出为：
$$a_1^{(2)}=\sigma (z_1^{(2)})=\sigma (w_{11}^{(2)}{x}_1+w_{12}^{(2)}{x}_2+w_{13}^{(2)}{x}_3+b_1^{(2)})$$

$$a_2^{(2)}=\sigma (z_2^{(2)})=\sigma (w_{21}^{(2)}{x}_1+w_{22}^{(2)}{x}_2+w_{23}^{(2)}{x}_3+b_2^{(2)})$$

$$a_3^{(2)}=\sigma (z_3^{(2)})=\sigma (w_{31}^{(2)}{x}_1+w_{32}^{(2)}{x}_2+w_{33}^{(2)}{x}_3+b_3^{(2)})$$

对于第三层，它的输入是第二层的激活值（输出值）→$[a_1^{(2)},a_2^{(2)},a_3^{(2)}{]}^T$，同时这是输出层 $\mathbf{y}=[y_1,y_2{]}^T$，它的输出为：
$$y_1=a_1^{(3)}=\sigma (z_1^{(3)})=\sigma (w_{11}^{(3)}{a}_1^{(2)}+w_{12}^{(3)}{a}_2^{(2)}+w_{13}^{(3)}{a}_3^{(2)}+b_1^{(3)})$$

$$y_2=a_2^{(3)}=\sigma (z_2^{(3)})=\sigma (w_{21}^{(3)}{a}_1^{(2)}+w_{22}^{(3)}{a}_2^{(2)}+w_{23}^{(3)}{a}_3^{(2)}+b_2^{(3)})$$

若将式子推广到第 $l$ 层第 $j$ 个神经元，设第 $l-1$ 层有 $N_{l-1}$ 个神经元，则有：
$$a_j^{(l)}=\sigma (z_j^{(l)})=\sigma (\sum _{i\in N_{l-1}}{w}_{ji}^{(l)}{a}_i^{(l-1)}+b_j^{(l)})$$

用公式来表示各层的输入输出关系过于复杂，我们不妨使用矩阵来代替。假设第 $l-1$ 层有 $n$ 个神经元，第 $l$ 层有 $m$ 个神经元，规定从第 $l-1$ 层的第 $k$ 个神经元到第 $l$ 层的第 $j$ 个神经元的权重为 $w_{jk}^{(l)}$，第 $l$ 层的偏差 $b$ 组成向量 ${\mathbf{b}}^{(l)}\in R^{m\times 1}$
$${\mathbf{W}}^{(l)}=\left[\begin{array}{cccc}{w}_{11}^{(l)}& w_{12}^{(l)}& \cdots & w_{1n}^{(l)}\\ w_{21}^{(l)}& w_{22}^{(l)}& \cdots & w_{2n}^{(l)}\\ ⋮& ⋮& \ddots & ⋮\\ w_{m1}^{(l)}& w_{m2}^{(l)}& \cdots & w_{mn}^{(l)}\end{array}\right]=\left[\begin{array}{c}{\mathbf{w}}_1^{(l)}\\ {\mathbf{w}}_2^{(l)}\\ ⋮\\ {\mathbf{w}}_m^{(l)}\end{array}\right]，{\mathbf{b}}^{(l)}=\left[\begin{array}{c}{b}_1^{(l)}\\ b_2^{(l)}\\ ⋮\\ b_m^{(l)}\end{array}\right]$$

上式表示，第 $l-1$ 层到第 $l$ 层第 $j$ 个节点的权重 ${\mathbf{w}}_j^{(l)}$ 构成矩阵 ${\mathbf{W}}^{(l)}\in R^{m\times n}$

第 $l$ 层的线性回归值为向量 ${\mathbf{z}}^{(l)}$，激活值（输出值）为向量 ${\mathbf{a}}^{(l)}$
$${\mathbf{z}}^{(l)}=\left[\begin{array}{c}{z}_1^{(l)}\\ z_2^{(l)}\\ ⋮\\ z_m^{(l)}\end{array}\right]，{\mathbf{a}}^{(l)}=\left[\begin{array}{c}{a}_1^{(l)}\\ a_2^{(l)}\\ ⋮\\ a_m^{(l)}\end{array}\right]$$

则第 $l$ 层的输出用矩阵可以表示为：
$${\mathbf{a}}^{(l)}=\sigma ({\mathbf{z}}^{(l)})=\sigma ({\mathbf{W}}^{(l)}{\mathbf{a}}^{(l-1)}+{\mathbf{b}}^{(l)})$$

其中，$\sigma ({\mathbf{z}}^{(l)})$ 表示 ${\mathbf{z}}^{(l)}$ 中的每个元素分别代入函数 $\sigma (x)$ 中分别得到一个值，即 ${\mathbf{z}}_{(m\times 1)}^{(l)}⟹\sigma (x)⟹{\mathbf{a}}_{(m\times 1)}^{(l)}$

3.神经网络损失函数的反向传播(Back Propagation-BP)

在本节中，蓝字公式是非常重要的结论

在 神经网络(NN) 模型的超参数设置完成后，需要对模型各权重和偏差进行更新，由于存在多层的网络结构，因此无法直接对中间的隐藏层层利用损失值来更新权重，但可以利用损失从后到前的反向传播来进行参数的估计，即反向传播求导

设输入特征向量为 $\mathbf{x}=[x_1,x_2,...,x_n{]}^T$，各层权重为矩阵 ${\mathbf{W}}^{(l)}$，各层偏差为 ${\mathbf{b}}^{(l)}$，网络总层数为 $L$（即第 $L$ 层表示输出层），设输出节点个数为 $M$，其中 ${\mathbf{a}}^{(l)}$ 表示第 $l$ 层的输出向量，${\mathbf{z}}^{(l)}$ 表示第 $l$ 层的回归值的向量

同样地，我们通常引入均方误差损失函数来衡量模型的好坏，我们用矩阵和向量的形式来表达，则神经网络的损失为：
$$J(\mathbf{W},\mathbf{b})=\frac{1}{2}\sum _{j=1}^M(a_j^{(L)}-y_j^{(i)}{)}^2=\frac{1}{2}\sum _{j=1}^M\left[\begin{array}{c}(a_1^{(L)}-y_1^{(i)}{)}^2\\ (a_2^{(L)}-y_2^{(i)}{)}^2\\ ⋮\\ (a_M^{(L)}-y_M^{(i)}{)}^2\end{array}\right]=\frac{1}{2}\mid \mid ({\mathbf{a}}^{(L)}-{\mathbf{y}}^{(i)}{)}^2\mid \mid$$

其中，$a_j^{(L)}$ 表示第 $L$ 层（输出层）的第 $j$ 个节点的输出值，$y_j^{(i)}$ 表示第 $i$ 个样本标签向量 ${\mathbf{y}}^{(i)}$ 中第 $j$ 个元素（对应第 $j$ 个输出节点的预测值），而损失 $J(\mathbf{W},\mathbf{b})$ 就是所有节点预测值和真实值差距的总和，$||\mathbf{x}||$ 表示列向量 $\mathbf{x}$ 的 1-范数，即 ${\sum }_i{x}_i$

对于第 $L$ 层是输出层，其所有输出节点组成的向量为：
$${\mathbf{a}}^{(L)}=\sigma ({\mathbf{z}}^{(L)})=\sigma ({\mathbf{W}}^{(L)}{\mathbf{a}}^{(L-1)}+{\mathbf{b}}^{(L)})$$

$$于是：J(\mathbf{W},\mathbf{b})=\frac{1}{2}\mid \mid ({\mathbf{a}}^{(L)}-{\mathbf{y}}^{(i)}{)}^2\mid \mid =\frac{1}{2}\mid \mid {\left(\sigma ({\mathbf{W}}^{(L)}{\mathbf{a}}^{(L-1)}+{\mathbf{b}}^{(L)})-{\mathbf{y}}^{(i)}\right)}^2\mid \mid$$

损失函数 $J(\mathbf{W},\mathbf{b})$ 对第 $L$ 层第 $j$ 个节点的权重 ${\mathbf{w}}_j^{(L)}$ 和偏差 $b_j^{(L)}$ 的梯度由下式给出：
$$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_j^{(L)}}=\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial a_j^{(L)}}\frac{\partial a_j^{(L)}}{\partial z_j^{(L)}}\frac{\partial z_j^{(L)}}{\partial {\mathbf{w}}_j^{(L)}}$$

$$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial b_j^{(L)}}=\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial a_j^{(L)}}\frac{\partial a_j^{(L)}}{\partial z_j^{(L)}}\frac{\partial z_j^{(L)}}{\partial b_j^{(L)}}$$

其中，由于 $J(\mathbf{W},\mathbf{b})=\frac{1}{2}{\sum }_{j=1}^{N_L}(a_j^{(L)}-y_j^{(i)}{)}^2$，只有第 $j$ 项含 ${\mathbf{w}}_j^{(L)}$，因此，$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_j^{(L)}}$ 只与第 $j$ 项有关，其他项对 ${\mathbf{w}}_j^{(L)}$ 求导均为 $0$，即：
$$\begin{array}{rl}\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_j^{(L)}}& =\frac{1}{2}\frac{\partial (a_j^{(L)}-y_j^{(i)}{)}^2}{\partial {\mathbf{w}}_j^{(L)}}=\frac{1}{2}\frac{\partial {\left[\sigma (z_j^{(L)})-y_j^{(i)}\right]}^2}{\partial {\mathbf{w}}_j^{(L)}}\\ & =\frac{1}{2}\frac{\partial }{\partial {\mathbf{w}}_j^{(L)}}{\left[\sigma ({\mathbf{w}}_j^{(L)}\cdot {\mathbf{a}}^{(L-1)}+b_j^{(L)})-y_j^{(i)}\right]}^2\end{array}\text{\hspace{1em}(Ⅰ)}$$

同理，只有第 $j$ 项含 $b_j^{(L)}$，因此，$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial b_j^{(L)}}$ 只与第 $j$ 项有关，其他项对 $b_j^{(L)}$ 求导均为 $0$，即：
$$\begin{array}{rl}\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial b_j^{(L)}}& =\frac{1}{2}\frac{\partial (a_j^{(L)}-y_j^{(i)}{)}^2}{\partial b_j^{(L)}}=\frac{1}{2}\frac{\partial {\left[\sigma (z_j^{(L)})-y_j^{(i)}\right]}^2}{\partial b_j^{(L)}}\\ & =\frac{1}{2}\frac{\partial }{\partial b_j^{(L)}}{\left[\sigma ({\mathbf{w}}_j^{(L)}\cdot {\mathbf{a}}^{(L-1)}+b_j^{(L)})-y_j^{(i)}\right]}^2\end{array}\text{\hspace{1em}(Ⅱ)}$$

因此，根据式 (Ⅰ) (Ⅱ)，损失函数 $J(\mathbf{W},\mathbf{b})$ 对第 $L$ 层第 $j$ 个节点的权重 ${\mathbf{w}}_j^{(L)}$ 和偏差 $b_j^{(L)}$ 的梯度可由下式给出：
$$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_j^{(L)}}=\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial a_j^{(L)}}\frac{\partial a_j^{(L)}}{\partial z_j^{(L)}}\frac{\partial z_j^{(L)}}{\partial {\mathbf{w}}_j^{(L)}}=(a_j^{(L)}-y_j^{(i)}){\sigma }^{\prime }(z_j^{(L)})({\mathbf{a}}^{(L-1)}{)}^T$$

$$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial b_j^{(L)}}=\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial a_j^{(L)}}\frac{\partial a_j^{(L)}}{\partial z_j^{(L)}}\frac{\partial z_j^{(L)}}{\partial b_j^{(L)}}=(a_j^{(L)}-y_j^{(i)}){\sigma }^{\prime }(z_j^{(L)})\cdot 1$$

其中，${\sigma }^{\prime }(z_j^{(L)})$ 表示直接将 $z_j^{(L)}$ 代入函数 ${\sigma }^{\prime }(x)$ 得到值即可

上述两式子有公共部分，将公共部分表示出来：
$${\delta }_j^L=(a_j^{(L)}-y_j^{(i)}){\sigma }^{\prime }(z_j^{(L)})=\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial a_j^{(L)}}\frac{\partial a_j^{(L)}}{\partial z_j^{(L)}}=\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial z_j^{(L)}}$$

（结论1） 若将第 $L$ 层所有的节点的 ${\delta }_j^L$ 合成一个向量 ${\delta }^L$，则有：
$${\delta }^L=\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{z}}^{(L)}}={\left[\begin{array}{c}{\delta }_1^L\\ {\delta }_2^L\\ ⋮\\ {\delta }_M^L\end{array}\right]}_{(M\times 1)}={\left[\begin{array}{c}(a_1^{(L)}-y_1^{(i)}){\sigma }^{\prime }(z_1^{(L)})\\ (a_2^{(L)}-y_2^{(i)}){\sigma }^{\prime }(z_2^{(L)})\\ ⋮\\ (a_M^{(L)}-y_M^{(i)}){\sigma }^{\prime }(z_M^{(L)})\end{array}\right]}_{(M\times 1)}=\underset{(M\times 1)}{\left({\mathbf{a}}^{(L)}-{\mathbf{y}}^{(i)}\right)}\ast \underset{(M\times 1)}{{\sigma }^{\prime }({\mathbf{z}}^{(L)})}$$

${\sigma }^{\prime }({\mathbf{z}}^{(L)})$ 表示 ${\mathbf{z}}^{(L)}$ 中的每个元素分别代入函数 ${\sigma }^{\prime }(x)$ 中分别得到一个值，即 ${\mathbf{z}}_{(M\times 1)}^{(L)}⟹{\sigma }^{\prime }(x)⟹{\mathbf{a}}_{(M\times 1)}^{(L)}$；其中，$M$ 为第 $L$ 层的节点个数，$\ast$ 表示哈达玛积

因此，若损失函数 $J(\mathbf{W},\mathbf{b})$ 对第 $L$ 层第 $j$ 个节点的权重 ${\mathbf{w}}_j^{(L)}$ 和偏差 $b_j^{(L)}$ 的导数可以表示为：
$$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_j^{(L)}}={\delta }_j^L({\mathbf{a}}^{(L-1)}{)}^T$$

$$\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial b_j^{(L)}}={\delta }_j^L$$

（结论2） 将所有的 $J(\mathbf{W},\mathbf{b})$ 对第 $L$ 层第 $j$ 个节点的权重 ${\mathbf{w}}_j^{(L)}$ 和偏差 $b_j^{(L)}$ 的导数合并成为一个最终的矩阵或列向量：
$${\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{W}}^{(L)}}}_{(M\times N)}=\left[\begin{array}{c}\frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_1^{(L)}}\\ \frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_2^{(L)}}\\ ⋮\\ \frac{\partial J(\mathbf{W},\mathbf{b})}{\partial {\mathbf{w}}_M^{(L)}}\end{array}\right]={\left[\begin{array}{c}{\delta }_1^L({\mathbf{a}}^{(L-1)}{)}^T\\ {\delta }_2^L({\mathbf{a}}^{(L-1)}{)}^T\\ ⋮\\ {\delta }_M^L({\mathbf{a}}^{(L-1)}{)}^T\end{array}\right]}_{(M\times N)}=\underset{(M\times N)}{{\delta }^L({\mathbf{a}}^{(L-1)}{)}^T}=\underset{(M\times 1)}{\left[\left({\mathbf{a}}^{(L)}-{\mathbf{y}}^{(i)}\right)\ast {\sigma }^{\prime }({\mathbf{z}}^{(L)})\right]}\underset{(N\times 1{)}^T}{({\mathbf{a}}^{(L-1)}{)}^T}$$

∂ J ( W , b ) ∂ b ( L ) ( M × 1 ) = [ ∂ J ( W , b ) ∂ b 1 ( L ) ∂ J ( W , b ) ∂ b 2 ( L ) ⋮ ∂ J ( W , b ) ∂ b M ( L ) ] = [ δ 1 L δ 2 L ⋮ δ M L ] ( M × 1 ) = [ ( a 1 ( L ) − y 1 ( i ) )   σ ′ ( z 1 ( L ) ) ( a 2 ( L ) − y 2 ( i ) )   σ ′ ( z 2 ( L ) ) ⋮ ( a M ( L ) − y M ( i ) )   σ ′ ( z M ( L ) ) ] ( M × 1 ) = ( a ( L ) − y ( i ) )