粒子群算法PSO(学习笔记_01)
1. 特点
-
高效的并行搜索算法
-
速度-位移模型简单易行
-
每个粒子在算法结束时仍保持其个体极值(除了得到最优解外,还可以得到若干较好的次优解,可用于调度、决策问题)
-
记忆功能(搜索行为在受其他个体影响的同时也受自身经验的引导)
2. 基本参数
-
m = 100; %粒子数量
-
d = 2; %粒子维度
-
iter_max = 200; %迭代次数
-
c1 = 1.5; %加速系数(认知)
-
c2 = 1.5; %加速系数(社会)
-
w: 惯性权重,w∈[w_min,w_max],通常情况下,w_max = 0.9 ,w_min = 0.4
-
v: 个体速度,v∈[v_min,v_max]
-
x: 个体的位置,x∈[x_min,x_max]
3. 基本流程
-
初始化:
-
每个粒子的位置和速度
-
初始化个体最优位置,最优值
-
初始化全局最优位置,最优值
-
-
for i = 1:iter_max
1. 计算每个粒子的个体最优值
2. 计算整个群体的全局最优值
3. 对粒子的速度、位置进行更新
4. 进行边界处理
end
- 输出结果
4. 基本粒子群算法
w = 1;
v(j,:) = v(j,:) + c1 * rand * (p(j,:) - x(j,:)) + c2 * rand * (g-x(j,:));5. 标准粒子群算法
v(j,:) = w * v(j,:) + c1 * rand * (p(j,:) - x(j,:)) + c2 * rand * (g-x(j,:));-
固定权重:通常情况下,w∈[0.8,1.2]
-
时变权重:w = w_max - (w_max - w_min) * i / iter_max;
-
源代码如下:
%% 标准粒子群算法
clear;
close all;
clc;
m = 100; %粒子数量
d = 2; %粒子维度
iter_max = 200; %迭代次数
c1 = 1.5; %加速系数(认知)
c2 = 1.5; %加速系数(社会)
w_max = 0.8; %惯性权重
w_min = 0.4;
v_max = 1; %个体的速度
v_min = -1;
x_max = 4; %个体的位置
x_min = -4;
%% 1、初始化
x = rand(m,d) * (x_max - x_min) + x_min;
v = rand(m,d) * (v_max - v_min) + v_min;
%% 初始化个体最优位置,最优值
p = x; %每个粒子的个体最优解的位置
pbest = ones(m,1)
for i =1:m
pbest(i) = func(x(i,:));
end
%% 初始化全局最优位置,最优值
g = ones(1,d); %全局最优位置
gbest = inf;
for i=1:m
if(pbest(i) < gbest)
g = p(i,:)
gbest = pbest(i);
end
end
gb = ones(1,iter_max);
for i = 1:iter_max
for j = 1:m
%% 2、计算每个粒子的个体最优值
if (func(x(j,:)) < pbest(j))
p(j,:) = x(j,:); %更新个体最优解位置
pbest(j) = func(x(j,:)); %更新个体最优解
end
%% 3、计算整个群体的全局最优值
if (pbest(j) < gbest)
g = p(j,:);
gbest = pbest(j);
end
%% 4、对粒子的速度、位置进行更新
w = w_max - (w_max - w_min) * i / iter_max; %时变权重
v(j,:) = w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
x(j,:) = x(j,:) + v(j,:);
%% 5、进行边界处理
for k = 1:d
if (v(j,k) > v_max | v(j,k) < v_min)
v(j,k) = rand * (v_max - v_min) + v_min;
end
if (x(j,k) > x_max | x(j,k) < x_min)
x(j,k) = rand * (x_max - x_min) + x_min;
end
end
end
gb(i) = gbest;
end
%g; %最优个体位置
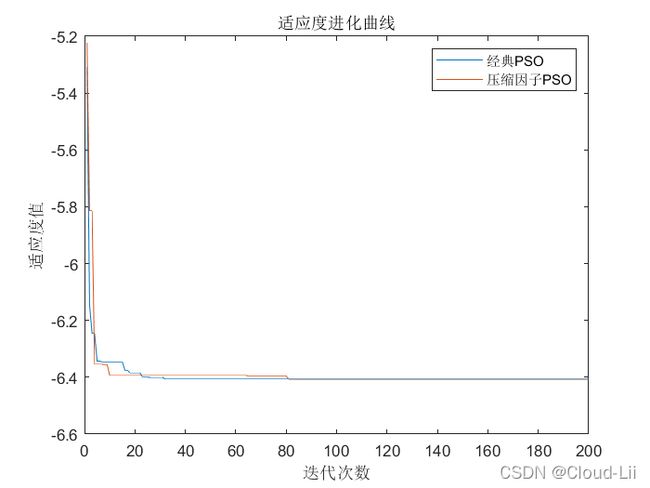
plot(gb)
hold on;
xlabel('迭代次数');
ylabel('适应度值');
title("适应度进化曲线");
legend_str = {'经典PSO','压缩因子PSO'};
function results = func(x)
results = 3*cos(x(1)*x(2))+x(1)+x(2)^2;
end
6. 压缩因子粒子群算法
-
Fai = c1 + c2;
-
压缩因子:Lamuda = 2/(abs(2-Fai-sqrt(FaiFai-4Fai)));
v(j,:) = Lamuda * v(j,:) + c1 * rand * (p(j,:) - x(j,:)) + c2 * rand * (g - x(j,:));-
源代码如下:
%% 压缩因子粒子群算法
m = 100; %粒子数量
d = 2; %粒子维度
iter_max = 200;
c1 = 1.5;
c2 = 1.5;
v_max = 1;
v_min = -1;
x_max = 4;
x_min = -4;
Fai = c1 + c2;
Lamuda = 2/(abs(2-Fai-sqrt(Fai*Fai-4*Fai))); %压缩因子
%% 1、初始化
x = rand(m,d) * (x_max - x_min) + x_min;
v = rand(m,d) * (v_max - v_min) + v_min;
%% 初始化个体最优位置,最优值
p = x; %每个粒子的个体最优解的位置
pbest = ones(m,1)
for i =1:m
pbest(i) = func(x(i,:));
end
%% 初始化全局最优位置,最优值
g = ones(1,d); %全局最优位置
gbest = inf;
for i=1:m
if(pbest(i) < gbest)
g = p(i,:)
gbest = pbest(i);
end
end
gb = ones(1,iter_max);
for i = 1:iter_max
for j = 1:m
%% 2、计算每个粒子的个体最优值
if (func(x(j,:)) < pbest(j))
p(j,:) = x(j,:); %更新个体最优解位置
pbest(j) = func(x(j,:)); %更新个体最优解
end
%% 3、计算整个群体的全局最优值
if (pbest(j) < gbest)
g = p(j,:);
gbest = pbest(j);
end
%% 4、对粒子的速度、位置进行进化
v(j,:) = Lamuda*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
x(j,:) = x(j,:) + v(j,:);
%% 5、进行边界处理
for k = 1:d
if (v(j,k) > v_max | v(j,k) < v_min)
v(j,k) = rand * (v_max - v_min) + v_min;
end
if (x(j,k) > x_max | x(j,k) < x_min)
x(j,k) = rand * (x_max - x_min) + x_min;
end
end
end
gb(i) = gbest;
end
%g; %最优个体位置
plot(gb)
legend(legend_str);
function results = func(x)
results = 3*cos(x(1)*x(2))+x(1)+x(2)^2;
end
7.离散粒子群算法
-
保留经典粒子群算法的速度-位置更新运算规则
-
粒子群在状态空间的取值和变化仅限于0、1,速度的每一维Vij表示位置Xij取值为1的可能性
-
位置更新等式:
-
vx(j,:) = 1./(1+exp(-v(j,:))); for k =1:d if vx(j,k) > rand x(j,k) = 1; else x(j,k) = 0; end end
-
源代码如下:
%% 离散粒子群算法
clear;
close all;
clc;
m = 100;
d = 20;
iter_max = 20;
c1 = 1.5;
c2 = 1.5;
w_max = 0.8;
w_min = 0.4;
v_max = 10;
v_min = -10;
x_max = 9;
x_min = 0;
%% 1.初始化
x = randi([0,1],m,d); %随机获取二进制编码的初始种群
v = rand(m,d) * (v_max - v_min) + v_min;
p = x;
pbest = ones(m,1);
for i = 1:m
pbest(i) = func(x(i,:),x_max,x_min);
end
g = ones(1,d);
gbest = inf;
for i = 1:m
if(pbest(i) < gbest)
g = p(i,:);
gbest = pbest(i);
end
end
for i = 1:iter_max
for j = 1:m
%更新个体最优
if(func(x(j,:),x_max,x_min) < pbest(j))
p(j,:) = x(j,:);
pbest(j) = func(x(j,:),x_max,x_min);
end
%更新整体最优
if(pbest(j) < gbest)
g = p(j,:);
gbest = pbest(j);
end
%更新速度
w = w_max - (w_max - w_min) * i / iter_max;
v(j,:) = w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
% 速度的边界处理
for k = 1:d
if (v(j,k) > v_max | v(j,k) < v_min)
v(j,k) = rand * (v_max - v_min) + v_min;
end
end
%更新位置
vx(j,:) = 1./(1+exp(-v(j,:)));
for k =1:d
if vx(j,k) > rand
x(j,k) = 1;
else
x(j,k) = 0;
end
end
end
gb(i) = gbest;
end
g; %最优个体
m = 0;
for i = 1:d
m = g(i) * 2^(i-1) + m;
end
f = x_min + m * (x_max - x_min)/(2^d - 1);
figure
plot(gb);
xlabel('迭代次数');
ylabel('适应度值');
title("适应度进化曲线")
function results = func(x,x_max,x_min)
m = 0;
d = length(x);
for i = 1:d
m = x(i) * 2^(i-1) + m;
end
f = x_min + m * (x_max - x_min)/(2^d - 1); %f即x(转换成十进制)
results = f + 6 * sin(4 * f) + 9 * cos(5 * f);
end