改进交叉算子的自适应人工蜂群黏菌算法
文章目录
- 一、理论基础
-
- 1、黏菌优化算法
- 2、多策略改进黏菌优化算法
-
- (1)自适应可调节反馈因子
- (2)算数交叉算子
- (3)改进的人工蜂群搜索策略
- (4)ISMA实现流程
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、黏菌优化算法
请参考这里。
2、多策略改进黏菌优化算法
(1)自适应可调节反馈因子
本文引入一种自适应可调节的反馈因子:在算法迭代前期,黏菌个体大范围感受食物浓度,此时食物浓度低,应该加快反馈因子的下降速度,减弱反馈关系,有利于提高算法全局搜索能力;在算法迭代后期,食物浓度高,此时应该保持较为平稳的反馈系数,有利于个体局部探索最高的食物浓度(最优解)。此外,加入下降速率调节因子 k k k,可以自动调节反馈因子下降速度,自适应可调节的反馈因子数学模型描述如式1所示: v c = ( e t max − t t max − 1 e − 1 ) k (1) v_c=\left(\frac{e^{\frac{t_{\max}-t}{t_{\max}}}-1}{e-1}\right)^k\tag{1} vc=(e−1etmaxtmax−t−1)k(1)其中, t t t为当前迭代次数, t max t_{\max} tmax为最大迭代次数, k k k是调节因子,线性反馈因子和调节参数 k k k分别取1、4和7时的自适应可调节反馈因子比较如图1所示。
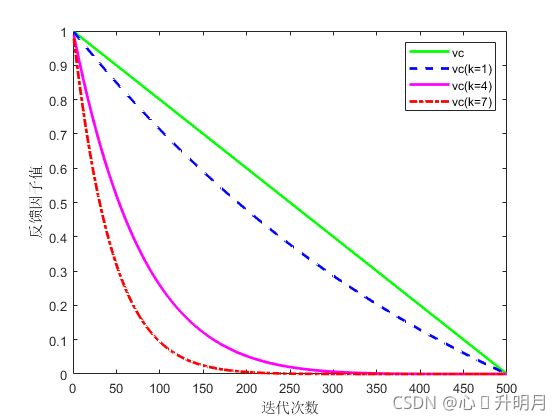
由图1可知,改进的反馈因子曲线的下降速度随着调节因子 k k k的增大而增大。在具体算法调试中, k k k值的选取不宜过大也不能太小, k k k值太大可能会导致算法前期收敛过快,算法开发能力减弱从而陷入局部极小值点;而 k k k值太小则不能体现反馈因子在平衡算法搜索能力上的优势,算法收敛速度变慢。为了平衡算法的搜索能力,本文经过大量实验分析,最后选取 k = 4 k=4 k=4最为合适。
(2)算数交叉算子
本文为了加快SMA的收敛速度,引入改进的算数交叉算子更新个体位置,即以一定的概率 P t P_t Pt让当前个体与种群最优个体进行交叉操作。交叉算子数学模型如式2所示: { X A 1 ( t + 1 ) = L ⋅ X A ( t ) + ( 1 − L ) ⋅ X b e s t ( t ) X A 2 ( t + 1 ) = L ⋅ X b e s t ( t ) + ( 1 − L ) ⋅ X A ( t ) (2) \begin{dcases}X_{A1}(t+1)=L\cdot X_A(t)+(1-L)\cdot X_{best}(t)\\X_{A2}(t+1)=L\cdot X_{best}(t)+(1-L)\cdot X_A(t)\end{dcases}\tag{2} {XA1(t+1)=L⋅XA(t)+(1−L)⋅Xbest(t)XA2(t+1)=L⋅Xbest(t)+(1−L)⋅XA(t)(2)其中, t t t为当前迭代次数, X A 1 X_{A1} XA1和 X A 2 X_{A2} XA2分别为交叉产生的两个子代个体位置, X A X_A XA为当前个体位置, X b e s t X_{best} Xbest为当前种群最优个体位置, L L L为取值 ( 0 , 1 ) (0,1) (0,1)的随机参数。
由式2可知,子代主要由父代和参数 L L L确定,其中参数 L L L控制子代从两个父代获取信息的比例,为了使子代获取更多优秀父代的基因,并保持种群多样性,本文改进了原始的随机参数,引入用拉普拉斯系数控制的参数 L L L。改进后的控制参数 L L L数学模型描述如式3所示: L = { μ − λ ⋅ ln ( r ) , r ≤ 1 2 μ + λ ⋅ ln ( r ) , r > 1 2 (3) L=\begin{dcases}\mu-\lambda\cdot\ln(r),\quad r≤\frac12\\\mu+\lambda\cdot\ln(r),\quad r>\frac12\end{dcases}\tag{3} L=⎩⎪⎨⎪⎧μ−λ⋅ln(r),r≤21μ+λ⋅ln(r),r>21(3)其中, μ \mu μ和 λ \lambda λ为拉普拉斯系数,其中 μ \mu μ取自然数,控制位置, λ > 0 \lambda>0 λ>0控制尺度, r r r为取值 [ 0 , 1 ] [0,1] [0,1]的随机数。由式3可知,改进后的参数 L L L通过引入系数λ调节父代与子代的距离, λ \lambda λ越小子代越靠近父代,种群多样性越高,同时,在拉普拉斯系数 μ \mu μ和 λ \lambda λ的共同调节下,子代能选择性获得更多优秀父代的位置信息。
(3)改进的人工蜂群搜索策略
针对SMA易早熟收敛的问题,本文引入人工蜂群搜索策略并做出改进,基本人工蜂群搜索策略数学模型描述如式4所示: Z i , j = x i , j + ϕ i , j ( x i , j − x k , j ) (4) Z_{i,j}=x_{i,j}+\phi_{i,j}(x_{i,j}-x_{k,j})\tag{4} Zi,j=xi,j+ϕi,j(xi,j−xk,j)(4)其中, Z i , j Z_{i,j} Zi,j为产生的候选解, x i , j x_{i,j} xi,j为当前个体, x k , j x_{k,j} xk,j为随机个体, k k k和 j j j为随机参数, k ∈ { 0 , 1 , ⋯ , M } k\in\{0,1,\cdots,M\} k∈{0,1,⋯,M}, j ∈ { 1 , 2 , ⋯ , d } j\in\{1,2,\cdots,d\} j∈{1,2,⋯,d}, M M M为固定值, d d d表示维度,且 k ≠ i k≠i k=i, ϕ i , j \phi_{i,j} ϕi,j为取值 [ − 1 , 1 ] [-1,1] [−1,1]的随机数。由式4可知,候选解由随机选取两个个体进行差分操作产生。
虽然人工蜂群搜索策略在搜索能力上有着很大的优势,但是其开发能力不强,因此本文引入一种新的搜索策略,在人工蜂群强大搜索能力的基础上加入全局最优位置引导,从而提高其开发能力,改进策略数学模型描述如式5所示: Z i , j = x i , j + ϕ i , j ( x i , j − x k , j ) + Ω i , j ( p g , j − x i , j ) (5) Z_{i,j}=x_{i,j}+\phi_{i,j}(x_{i,j}-x_{k,j})+\Omega_{i,j}(p_{g,j}-x_{i,j})\tag{5} Zi,j=xi,j+ϕi,j(xi,j−xk,j)+Ωi,j(pg,j−xi,j)(5)其中, Ω \Omega Ω为取值 [ 0 , 1.5 ] [0,1.5] [0,1.5]的随机值, p g p_g pg为全局最优位置。 \newline \newline
综上所述,本文在SMA迭代过程中引入改进的人工蜂群搜索策略,在每一次迭代结束时,对于原始算法更新产生的个体和引入人工蜂群策略生成的个体,采用贪婪策略保留其中较优的个体,加快算法收敛,同时,人工蜂群搜索策略强大的搜索能力可以减少局部极值点对SMA的影响,从而提高算法跳出局部最优解的能力。
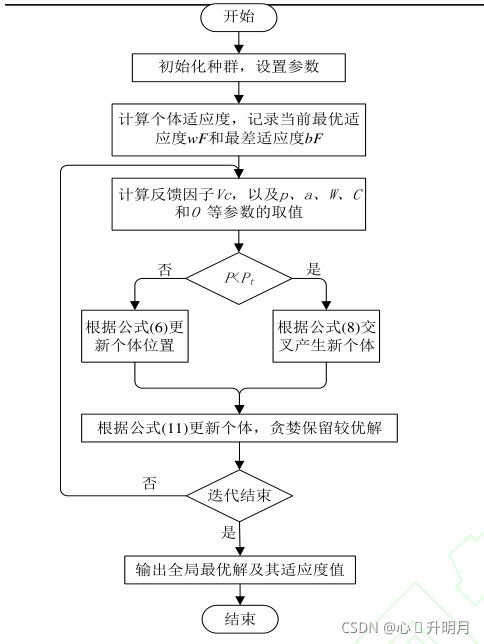
(4)ISMA实现流程
二、仿真实验与结果分析
本文选取粒子群优化(PSO)算法、灰狼优化(GWO)算法、鲸鱼优化算法(WOA)和SMA与ISMA进行实验对比,基本参数统一设置为:最大迭代次数 t max = 500 t_{\max}=500 tmax=500,维度 d = 30 d=30 d=30,种群规模 N = 30 N=30 N=30,算法寻优执行30次。各算法内部参数设置如文献[1]中表1所示。以文献[1]中表2的8个基准测试函数为例,结果显示如下:





函数:F1
SMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
PSO:最差值: 1523.6253,最优值:513.6694,平均值:953.8162,标准差:250.2809,秩和检验:1.2118e-12
GWO:最差值: 7.9819e-27,最优值:4.3317e-30,平均值:1.2354e-27,标准差:2.0606e-27,秩和检验:1.2118e-12
WOA:最差值: 5.0442e-70,最优值:2.0869e-89,平均值:1.7291e-71,标准差:9.2037e-71,秩和检验:1.2118e-12
ISMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
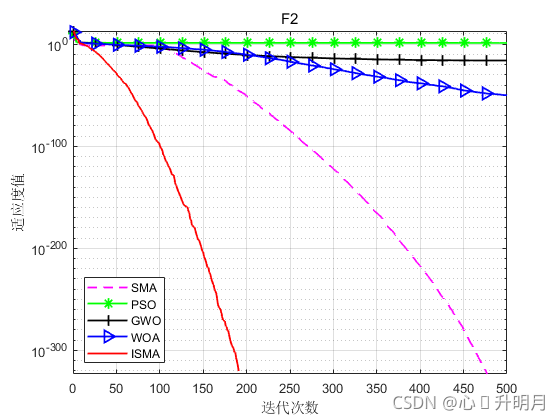
函数:F2
SMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
PSO:最差值: 28.3793,最优值:9.9685,平均值:16.7905,标准差:4.7645,秩和检验:1.2118e-12
GWO:最差值: 2.6669e-16,最优值:2.0505e-17,平均值:9.9426e-17,标准差:6.7665e-17,秩和检验:1.2118e-12
WOA:最差值: 1.2918e-49,最优值:8.4789e-57,平均值:8.5277e-51,标准差:2.7953e-50,秩和检验:1.2118e-12
ISMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数:F3
SMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
PSO:最差值: 8826.0365,最优值:1636.6971,平均值:4983.8735,标准差:1882.2474,秩和检验:1.2118e-12
GWO:最差值: 9.5503e-05,最优值:1.992e-08,平均值:1.4961e-05,标准差:2.4536e-05,秩和检验:1.2118e-12
WOA:最差值: 78762.8684,最优值:24704.079,平均值:43320.671,标准差:12421.3933,秩和检验:1.2118e-12
ISMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数:F4
SMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
PSO:最差值: 27.6284,最优值:11.3731,平均值:19.5063,标准差:4.5492,秩和检验:1.2118e-12
GWO:最差值: 2.7847e-06,最优值:7.8886e-08,平均值:6.5497e-07,标准差:6.8193e-07,秩和检验:1.2118e-12
WOA:最差值: 90.8403,最优值:0.47206,平均值:52.4522,标准差:29.7559,秩和检验:1.2118e-12
ISMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数:F5
SMA:最差值: 0.0027292,最优值:0.00037931,平均值:0.0010421,标准差:0.00052546,秩和检验:0.0083146
PSO:最差值: 1727.8237,最优值:380.5853,平均值:861.2589,标准差:336.3319,秩和检验:3.0199e-11
GWO:最差值: 1.9986,最优值:0.2496,平均值:0.88063,标准差:0.45627,秩和检验:6.0658e-11
WOA:最差值: 1.5867,最优值:0.06534,平均值:0.42383,标准差:0.33896,秩和检验:2.8314e-08
ISMA:最差值: 0.37681,最优值:7.2427e-07,平均值:0.061695,标准差:0.11179,秩和检验:1
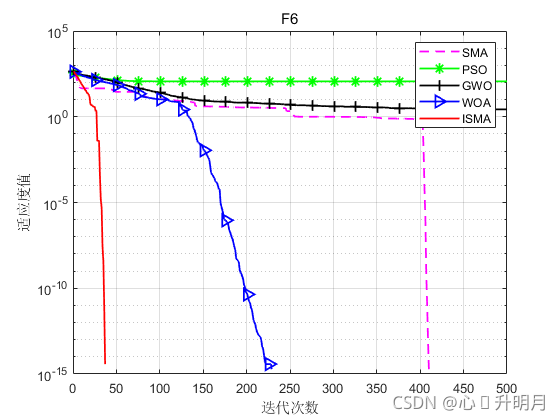
函数:F6
SMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
PSO:最差值: 168.9792,最优值:79.4786,平均值:116.1969,标准差:20.9312,秩和检验:1.2118e-12
GWO:最差值: 12.0808,最优值:5.6843e-14,平均值:2.6837,标准差:3.5627,秩和检验:1.1757e-12
WOA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
ISMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
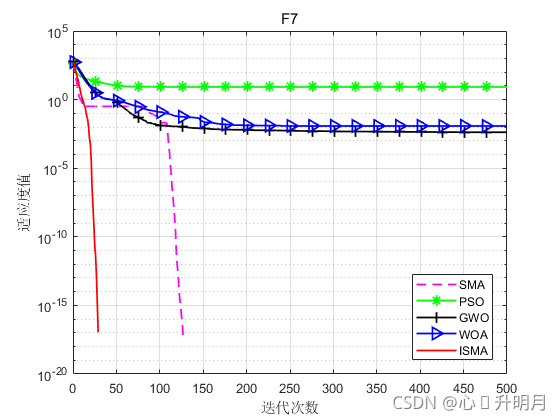
函数:F7
SMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
PSO:最差值: 16.7232,最优值:4.07,平均值:8.3089,标准差:3.4772,秩和检验:1.2118e-12
GWO:最差值: 0.025467,最优值:0,平均值:0.0041322,标准差:0.0075889,秩和检验:0.002788
WOA:最差值: 0.18785,最优值:0,平均值:0.011997,标准差:0.045703,秩和检验:0.1608
ISMA:最差值: 0,最优值:0,平均值:0,标准差:0,秩和检验:NaN
函数:F8
SMA:最差值: 0.22234,最优值:9.7935e-05,平均值:0.079872,标准差:0.05841,秩和检验:1.5292e-05
PSO:最差值: 93.9565,最优值:4.2147,平均值:29.2768,标准差:19.807,秩和检验:3.0199e-11
GWO:最差值: 0.16863,最优值:0.0066064,平均值:0.047953,标准差:0.034743,秩和检验:7.1988e-05
WOA:最差值: 0.08056,最优值:0.0056718,平均值:0.02224,标准差:0.015719,秩和检验:0.8418
ISMA:最差值: 0.05388,最优值:1.4525e-07,平均值:0.020084,标准差:0.016304,秩和检验:1
结果表明,改进的算法具有很好的鲁棒性和寻优性能。
三、参考文献
[1] 刘成汉, 何庆. 改进交叉算子的自适应人工蜂群黏菌算法[J/OL]. 小型微型计算机系统: 1-8 [2021-11-16].