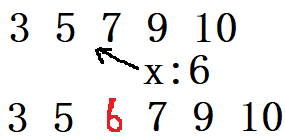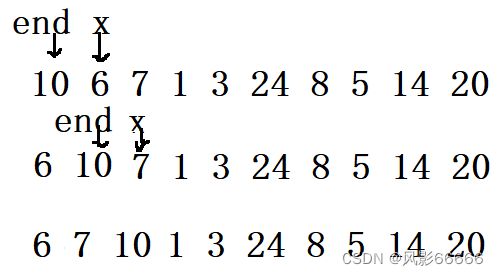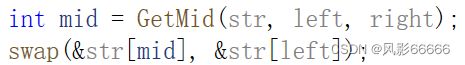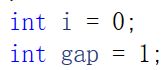八大常用排序

目录

前言

一、插入排序

二、希尔排序

三、选择排序

四、堆排序

五、冒泡排序

六、快速排序

七、归并排序

八、计数排序

九、稳定性

---

前言

此篇博客都是以升序为例，降序只需更改部分地方即可，所以只排一个

一、插入排序

单趟排序

如上图，在一个有序数组中插入一个6，只要找到比6小的数，此数后面的数往后挪动，然后在其后插入6即可 

整个插入排序

外面只需套一层循环即可，为了保证不越界，所以i最多只能是倒数第二个元素的下标

如上图，起初可将第一个数看成是有序的，第二个数就是待插入的数，比它小就往前放，比它大就跳出循环，然后就是前2个数有序、前三个数有序……前n-1个数有序等等

二、希尔排序

希尔排序是在插入排序的基础上加强的

核心思路就是先分组，然后让每一组的数据都有序，最后再插入排序即可

设gap=3，即分3组

单趟排序与插入排序类似，只是把+1/-1改为了+gap/-gap，下图是第一组的排序

如下图，外面套一层for循环，就能把其它组进行排序了，循环判断条件n-gap,保证还留一组在外，i取不到，是为了保证不会越界，while循环是为了进行多次预排，gap=1时，就是插入排序

(也能不要while循环，直接将gap赋初值为3或其它数)

 

三、选择排序

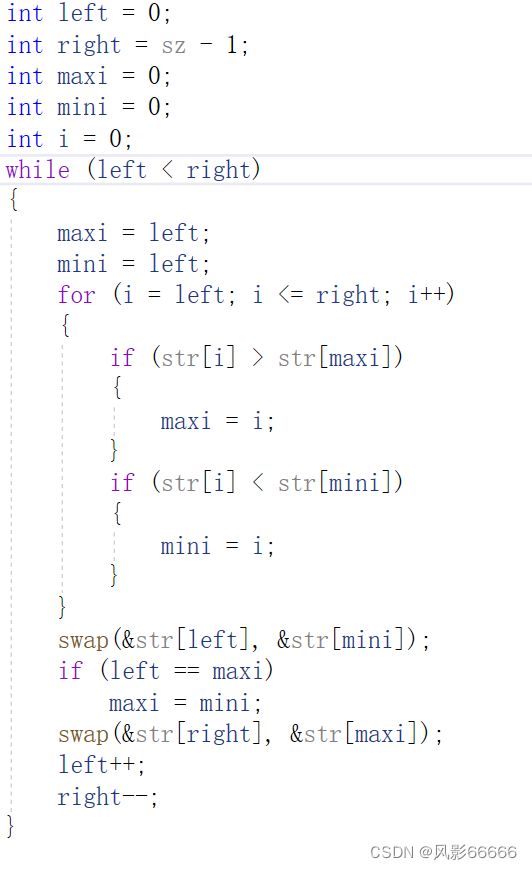
如上图，采用的是头尾双指针，头指针找小，尾指针找到，然后两者交换即可

如上图，最后面加一个if语句是为了防止第一个数就是最大数，会被换走 

四、堆排序

首先得写一个向下调整的函数(向上调整也行)

 因为是排升序，所以建大堆比较好

因为大堆根节点是最大的数，所以将其与最后一个数交换，然后将n-1个数向下调整又成为一个新的大堆，多次如此即排序完成，当只有一个数时，就不需要排了，因为它是第一个数，也是最小的数，后面的数都是有序数组了

 

五、冒泡排序

单趟排序

两个数比较大小，小的就放前面，大的放后面，往后如此，最大的数就放在最后了

整个排序

再往外套一个循环，有n个数，就得走n-1趟，而每一趟比较的次数也是逐渐-1

定义一个变量flag，赋初值为1,表示假设它有序，当有比较交换时就赋值为0，表示无序，当走完一趟，flag还是1，就表示有序了，直接break跳出循环，结束排序即可，所以flag能提高效率

六、快速排序

hoare版本

首先创建左右两个指针，选左边作key，右边先走，右指针找小于指向key的值，左指针找大于指向key的值，当两个指针相遇时结束，然后将指向key的值与相遇指向的哪个值交换，这样key指向的值，左边都小于它，右边都大于它，最后返回相遇的下标(右边作key，左边先走)

有=是因为当数组的数据全是同一个数时会死循环

要加left

如果左边作key，左边先走，就会出问题，如下图

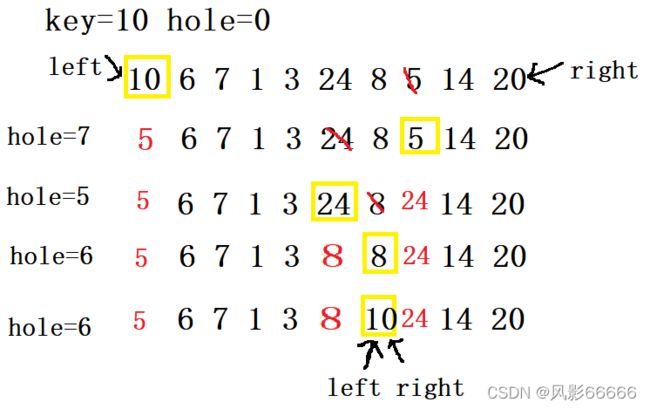
挖坑法

左边选key，还是右边先走，这次key是左边的第一个元素而不是下标，而坑位则是下标，起初是第一个元素的下标，当right遇到小时，就把该坐标的值赋值给坑位所在的数组成员，而该坐标则是新的坑位，同理，left也一样，left与right相遇结束，然后把key赋值给坑位所在的数组成员即可

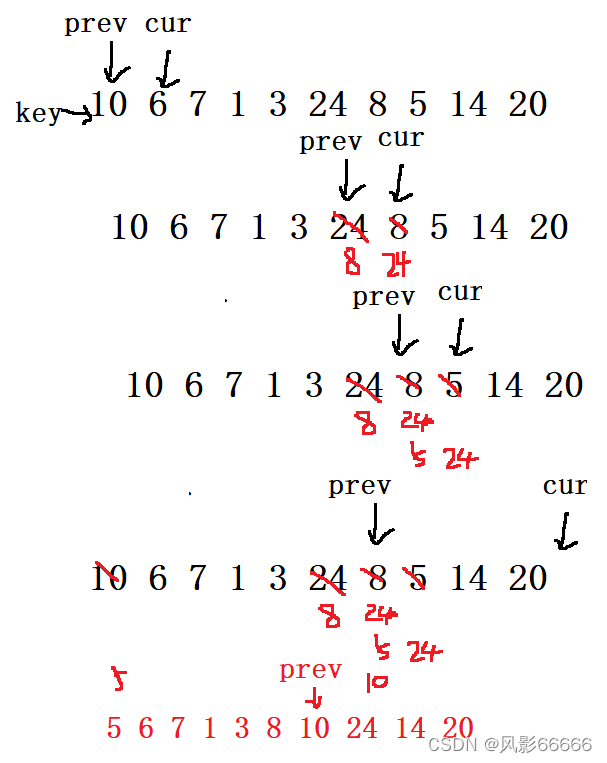
前后指针法

选左做key，定义两个指针cur和prev，cur在前，prev在后，cur找小于key指向的数据，当cur指向的数值一直为小时，prev就一直紧跟着，二者不发生交换，当二者经过了有比key指向的数据大时，再遇到小于key指向的数据时，才发生交换，当cur指向的数据不再是数组中的数据时结束，最后将prev指向的数据与key指向的数据交换

整个排序(递归)

把一大区间的排序分成多个左右小区间来排序，当只有left>=right时就结束

整个排序(非递归)

得借助栈来保存区间的两个端点

首先先存储开始大区间的两个端点

因为栈是后进先出，所以先用begin存储先出来的数据，用end存储后出来的数据

然后就可以调用函数找keyi了

此时就能分成两个区间，一个是[begin,keyi-1],另一个是[keyi+1,end],然后再把这两个区间的端点都放到栈中去，再取出即可

循环判断条件是栈中是否还有数据，即栈是否为空，最后销毁栈即可

  

快速排序优化

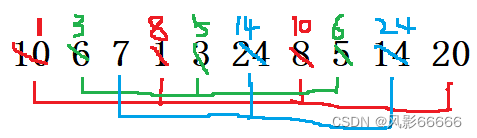
可以从左中右三个位置取出中间大小的数，然后与左边的数交换，再选左做key，能使其分为相对均衡的两个小区间，提高效率，比如数组是1 4 7 3 5 2 8 6 9，排升序

  

七、归并排序

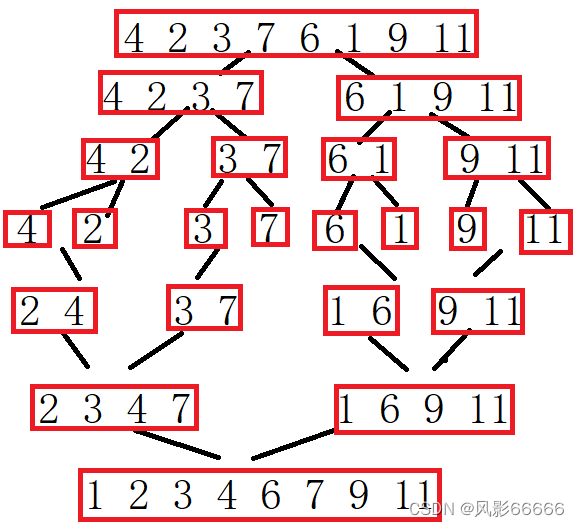
借助一个临时数组，将原数组分为2个区间，看成两个有序数组，再将其按照从小到大的顺序拷贝到临时数组中，而想要是有序数组，需要不断缩小区间，直到2个区间都各只有一个数时，就拷贝到临时数组中去，如下图

 

 

取中间坐标，将其化为小区间，再分别递归

 

两个区间从起始端点开始，逐渐比较大小，当有一个区间被拷贝完就结束循环

还有一个区间没拷贝完，所以仍需接着拷贝

 

拷贝完后，还需拷贝回原数组，因为需要从原数组中拿数据

如上图，一一归并后临时数组是2 4 3 7 1 6 9 11，原数组是4 2 3 7 6 1 9 11

两两归并时，两个区间都不是有序数组，就达不到目的，所以需拷贝回原数组

非递归

同样需借助临时数组

 

gap是分组，开始是分成n组，然后是n/2组等等，gap每次归完后是*2，如一一归完后gap就*2

 

一一归完后，二二归等等，所以要借助for循环，每次归完从头开始

index是拷贝到临时数组时，临时数组的下标

这里可以先每次归完后再拷贝回原数组，与递归有所差异

 

只有数组的数据个数和满二叉树的数据一样多时，才不会出现越界问题，所以需考虑越界

有三种越界，end1，begin2，end3越界

begin2越界时，只要使右区间不存在，就不会出现越界和后面循环重复拷贝的情形

八、计数排序

首先要从数组中找到它的最大值和最小值，从而用相对的方式来计数，不至于浪费空间，比如如果只找最大值，假如是900，最小值却是600，如果从0开始就得开辟901个数据的空间，而用下标为0存600，就只需要301个数据的空间，同时需借助临时数组，以及用memset将其全部置为0

然后计数，如600，下标为0的元素就表示600，有几个600该元素就+几，605，下标为5的元素就是605等等

从最小的数据开始取数据，有几个就取几个

 九、稳定性

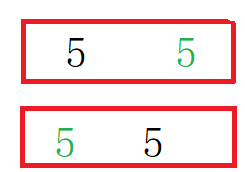
概念：同大小的数据在数组中的相对位置，如果发生变化就表示不稳定，没有发生变化就表示稳定

如下图，就表示不稳定

插入排序、冒泡排序、归并排序是稳定的，没有改变相对位置

而希尔排序不稳定，因为涉及分组，所以相对位置会发生变化

堆排序不稳定，如下图

选择排序也不稳定，如下图

快速排序也不稳定，如下图

计数排序不稳定