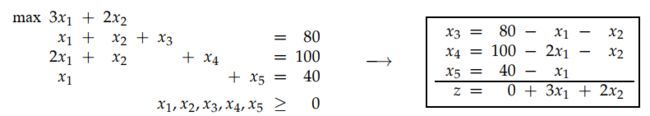LP问题进阶 Part 1 | 单纯形法

这一部分对应书上第四章（P16-P26），其难度比前三章大得多。个人建议先粗读了解这个方法的思路，再精读把握具体技巧。建议学习时间为2个小时。单纯形法是求解线性规划问题的通用方法，百度百科中有十分详细的说明，可以对照地阅读学习。

为方便查阅，再link一下教材。

---

基本概念

假设我们讨论的LP问题有个变量与个限制条件。

• 单纯形(Simplex) 和代数拓扑中的单形是一个单词，但是不清楚二者有没有关系。这里指的就是可行域在维空间中对应的那个图形，这里为求一般性提到了n维空间，但在学习的时候不妨假设，反正书上是这样默认的。此时单纯形对应的就是二维平面中的一个多边形。单纯形方法不是几何的（类比之前的作图法），但是借助几何可以更好地理解这一解法。

• LP问题的正则形式(Canonical form)是原LP问题的一种变形，满足：

  • 所有的限制条件都写为等号形式；
  • 所有的变量都是非负的。
  • 最大值问题
    其将原限制条件（可能是大于等于或小于等于）写为等式的方法是引入一个大于零的松弛变量(slack variable)。概念不难，详见P16最底下那块儿。值得注意的是一个限制条件至多只会引入一个松弛变量。
    下图是将LP化为正则形式的一个例子。
    
    

    将LP问题化为正则形式

• 基本解(Basic solution) 对于有个变量（包括松弛变量，与区别）与个限制条件的正则形式的LP问题，基本解的定义为至少有个变量为0的可行解

  • 基本解是一个重要的概念，不妨先不加理解地记住其定义。
  • 基本解对应的是可行域的顶点。（注意，可行解即可行域中的点）。
  • 每一个可行域的顶点都是基本解 这一点非常重要，但是书上只提到而没有详细说明。下面给出一种证明。

  Proof:
  观察：可行域的每一个顶点一定是个维平面的交（考虑线性方程组有唯一解的条件，对线性代数不是很熟悉的朋友可以先默认这一点。）。注意，反之不然。
  考虑任意个限制条件，不妨就考虑前n个。 不妨假设原LP问题的限制条件都为-条件。
  好像没我想象的那么简单，先不写了。

  • 基本解中被设置为0的变量被称为非基本变量(non-basic variable)，未被设置为0的则称为基本变量(basic variable)。这两个概念之后也要用到，注意不要记反了。
  • 所有的基本变量合在一起成为基(basis)。

• 字典(Dictionary)是一种表示、记录变量的方式，简单点说就是用非基本变量表示基本变量和目标函数。如图所示：

  

  箭头右边就是一种字典表示
  • 字典表示与基本变量的选取有关。

基本概念部分大概就是这些。第一次看不用要求自己完全理解，不妨先继续往下学习再慢慢理解这些概念。

---

思路简介

单纯形方法的示意图如下：

单纯形方法示意图

简单地说就是先找到一个可行解（假如存在的话），之后再不断地优化这个解。
具体地，为了对可行解进行优化，书上提到了一种操作。由于书上没有为这个操作命名，为方便起见，在此我们管这种操作叫“优化操作”。优化操作是单纯形方法的核心步骤，单纯形法说白了就是对一个基本解实施若干次优化操作后得到最优解的过程。下面我们来讨论什么是优化操作。

优化操作

我们先从一下四点直观的认识入手。

• 首先，优化操作将一个可行解变为另外一个可行解。
• 由于之前提到过可行域的顶点一定对应一个基本解，因此优化操作一定将基本解变换为基本解。
• 回忆基本解的定义，自然地可以想到优化操作调整变量的取值，将非基本变量变为基本变量，将基本变量变为非基本变量。
• 更加自然地可以想到：优化操作使得目标函数的取值增加。注意，一个解对应着目标函数的一个取值。

由于书上根本就没有优化操作的概念，所以在此我自己给出其定义：

定义 优化操作
优化操作给某一个非基本变量一非负增量，使得目标函数增加且使一个基本变量变为0。除此之外，不存在比该增量更小的增量使得该非基本变量加上此增量后存在一个基本变量为0。

我们称增加的这个非基本变量为输入变量，变为0的这个基本变量为输出变量。因为输入变量取代了输出变量成为新的基。（基的定义可以在前面找到。）
通俗一点地说就是选择一个非基本变量，让其不断增加，要求：

• 目标函数增加。注意，非基本变量增加时目标函数不一定增加。
• 当某一个基本变量变为0时停止。此即定义的第二句话。
  注意，由于如果一个变量的增加导致目标函数的增加以及另一个变量的减少，那么假如减少的变量可以无限制地减，则目标函数就会无限制地增。好在由定义可知每个变量都必须是非负的，所以这种情况不会发生。

回到主题。之前提到单纯形法即对一个基本解实施若干次优化操作后得到最优解的过程。我们先不考虑最优解的存在性，且断言：任意非基本变量增加不使得目标函数增加等价于目标函数取得最大值。这是因为由于符号的限制，非基本变量只能增加，而所有的变量都可以被非基本变量表示。因此非基本变量的增加包含了所有变量的各种变化。

当无法再进行优化操作时有两种可能。一种是任意非基本变量的增加不使得目标函数增加。此时目标函数取最大值。另外一种情况是任意非基本变量的增加不使得某一基本变量变为0。注意，LP问题的标准形式中对于变量的所有限制最终都会归结于符号限制，因此若基本变量不会变为0，则非基本变量可以无限地增加。此时LP问题无界。

还有一点需要注意的是优化操作一定会在有限步后结束，之后会讲到这一点。

经过上述讨论我们对单纯形算法的核心步骤应该有一个大致的了解了。

单纯形算法：实施步骤

下面是一个小小的总结

1. 准备工作

• 将LP问题化为正则形式。
• 找到一个基本解，建立初始字典。（具体方法书上P23有讲。）

2. 优化操作

• 如果目标函数中所有变量的系数都是负的，那么目标函数已经取最大值。此时将非基本变量设为0，借此解出基本变量与目标函数的值。返回这组值。
• 如果目标函数中存在正系数变量，取之为输入变量。如果无法进行优化操作，则LP问题无界。如果可以进行优化操作，那就进行一下优化操作。
• 建立对应的新字典，重复之前步骤。

单纯形算法到此结束

习题(P20)

1. 要挑选哪个变量作为输入变量，哪个作为输出变量？
   满足定义就行。
2. 优化操作是否会在有限步后结束？
   是。因为优化操作本质上是对可行域顶点的枚举，而顶点只有有限个，且不重复取到。不重复的原因是每一个顶点唯一地对应着目标函数的一个值，而优化算法使得目标函数增加。
3. 如何将其他LP问题形式转化为标准形式？
   这在第二章中讲过。
4. 如何找到初始字典？
   见书上第23页。