双向链表
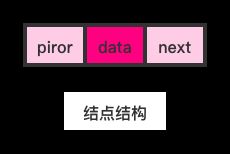
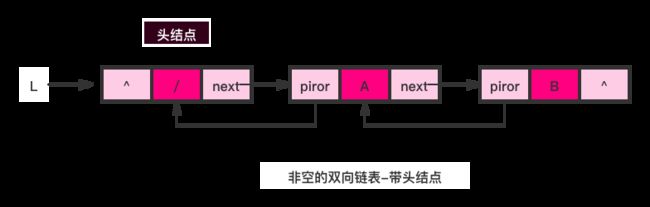
双向链表（双链表）是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继（next）和直接前驱（prior）。如果他为空，那么 next 和 prior 都指向自己。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。
结点结构.png
无头结点的非空的双向链表.png
带头结点的非空的双向链表.png
创建
宏定义
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码，如OK等 */
typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */
//定义结点
typedef struct Node {
ElemType data;
struct Node *prior;
struct Node *next;
} Node;
typedef struct Node * LinkList;
创建结点
Status createLinkList(LinkList *L) {
//*L 指向头结点
*L = (LinkList)malloc(sizeof(Node));
if (*L == NULL) return ERROR;
(*L)->prior = NULL;
(*L)->next = NULL;
(*L)->data = -1;
//新增数据
LinkList p = *L;
for(int i=0; i < 10; i++){
//1.创建1个临时的结点
LinkList temp = (LinkList)malloc(sizeof(Node));
temp->prior = NULL;
temp->next = NULL;
temp->data = I;
//2.为新增的结点建立双向链表关系
//① temp 是p的后继
p->next = temp;
//② temp 的前驱是p
temp->prior = p;
//③ p 要记录最后的结点的位置,方便下一次插入
p = p->next;
}
return OK;
}
插入
插入结点.png
插入.png
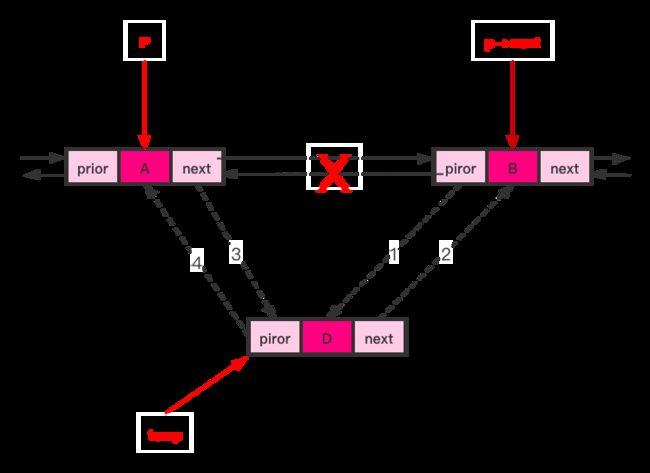
A：插入位置的前结点；B：插入位置的后结点；D：新结点
- 创建新结点 D；
- 找到插入位置的前一个结点 A；
- 判断是不是插入在尾结点之后，如果是，新结点 D 的 piror 指向尾结点 A，尾结点 B 的 next 指向新结点；如果不是，A 的 next 指向新结点 D，新结点 D 的 piror 指向 A，新结点 D 的 next 指向 B，B 的 piror 指向新结点 D。
Status ListInsert(LinkList *L, int i, ElemType data) {
//1. 插入的位置不合法 为0或者为负数
if (i < 1) return ERROR;
//2. 新建结点
LinkList temp = (LinkList)malloc(sizeof(Node));
temp->data = data;
temp->prior = NULL;
temp->next = NULL;
//3.将p指向头结点!
LinkList p = *L;
//4. 找到插入位置i直接的结点
for(int j = 1; j < i && p;j++)
p = p->next;
//5. 如果插入的位置超过链表本身的长度
if(p == NULL) {
return ERROR;
}
//6. 判断插入位置是否为链表尾部;
if (p->next == NULL) {
p->next = temp;
temp->prior = p;
}
else {
//将p->next 结点的前驱prior = temp
p->next->prior = temp;
//将temp->next 指向原来的p->next
temp->next = p->next;
//p->next 更新成新创建的temp
p->next = temp;
//新创建的temp前驱 = p
temp->prior = p;
}
return OK;
}
删除
删除需要判断是不是尾节点，因为尾节点的 next 需要设为 NULL。
删除结点.png
删除双向链表指定位置上的结点
Status ListDelete(LinkList *L, int i, ElemType *e) {
int k = 1;
LinkList p = (*L);
//1.判断双向链表是否为空,如果为空则返回ERROR;
if (*L == NULL) {
return ERROR;
}
//2. 将指针p移动到删除元素位置前一个
while (k < i && p != NULL) {
p = p->next;
k++;
}
//3.如果k>i 或者 p == NULL 则返回ERROR
if (k>i || p == NULL) {
return ERROR;
}
//4.创建临时指针delTemp 指向要删除的结点,并将要删除的结点的data 赋值给*e,带回到main函数
LinkList delTemp = p->next;
*e = delTemp->data;
//5. p->next 等于要删除的结点的下一个结点
p->next = delTemp->next;
//6. 如果删除结点的下一个结点不为空,则将将要删除的下一个结点的前驱指针赋值p;
if (delTemp->next != NULL) {
delTemp->next->prior = p;
}
//7.删除delTemp结点
free(delTemp);
return OK;
}
删除双向链表指定的元素
Status LinkListDeletVAL(LinkList *L, int data) {
LinkList p = *L;
//1.遍历双向循环链表
while (p) {
//2.判断当前结点的数据域和data是否相等,若相等则删除该结点
if (p->data == data) {
//修改被删除结点的前驱结点的后继指针,参考图上步骤1️⃣
p->prior->next = p->next;
//修改被删除结点的后继结点的前驱指针,参考图上步骤2️⃣
if(p->next != NULL){
p->next->prior = p->prior;
}
//释放被删除结点p
free(p);
//退出循环
break;
}
//没有找到该结点,则继续移动指针p
p = p->next;
}
return OK;
}
查找
- 从首元结点开始判断结点的 data 是否一致，不一致移动指针，指向下一个结点，直到指针指向的结点的 data 是我们需要的，返回。
int selectElem(LinkList L, ElemType elem) {
LinkList p = L->next;
int i = 1;
while (p) {
if (p->data == elem) {
return I;
}
I++;
p = p->next;
}
return -1;
}
更新
- 找到要操作的结点；
- 更新结点的 data。
Status replaceLinkList(LinkList *L, int index, ElemType newElem) {
LinkList p = (*L)->next;
for (int i = 1; i < index; i++) {
p = p->next;
}
p->data = newElem;
return OK;
}
双向循环链表
双向循环链表相对于双向链表而言，只需要最后一个元素的next指向head->next，head->next的prior指向最后一个节点即可。本质上还是一个双向链表，因此在双向循环链表中，依然能够找到头指针和头节点等。
双向非空循环链表.png
双向循环链表大体上实现是相同的，下面只针对不同的地方做一些说明。
双向循环链表的创建
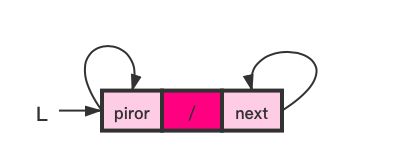
初始化时需要将头节点的next和prior都指向自己。
空的双向循环链表.png
Status creatLinkList(LinkList *L) {
*L = (LinkList)malloc(sizeof(Node));
if (*L == NULL) {
return ERROR;
}
(*L)->next = (*L); //指向自己
(*L)->prior = (*L); //指向自己
// 和双链表的处理类似
return OK;
}
双向循环链表的插入
- 当插入位置超过链表长度则插入到链表末尾；
- 不需要判断尾节点的 next 是否为 NULL，因为它会指向头节点。
Status LinkListInsert(LinkList *L, int index, ElemType e) {
//1. 创建指针p,指向双向链表头
LinkList p = (*L);
int i = 1;
//2.双向循环链表为空,则返回error
if(*L == NULL) return ERROR;
//3.找到插入前一个位置上的结点p
while (i < index && p->next != *L) {
p = p->next;
i++;
}
//4.如果i>index 则返回error
if (i > index) return ERROR;
//5.创建新结点temp
LinkList temp = (LinkList)malloc(sizeof(Node));
//6.temp 结点为空,则返回error
if (temp == NULL) return ERROR;
//7.将生成的新结点temp数据域赋值e.
temp->data = e;
//8.将结点temp 的前驱结点为p;
temp->prior = p;
//9.temp的后继结点指向p->next;
temp->next = p->next;
//10.p的后继结点为新结点temp;
p->next = temp;
//如果temp 结点不是最后一个结点
if (*L != temp->next) {
//11.temp节点的下一个结点的前驱为temp 结点
temp->next->prior = temp;
}
else {
(*L)->prior = temp;
}
return OK;
}
双向循环链表的删除
- 如果删除到只剩下首元结点了,则直接将*L置空；
- 不需要判断尾节点的 next 是否为 NULL，因为它会指向头节点。
Status LinkListDelete(LinkList *L,int index,ElemType *e) {
int i = 1;
LinkList temp = (*L)->next;
if (*L == NULL) {
return ERROR;
}
//如果删除到只剩下首元结点了,则直接将*L置空;
if(temp->next == *L){
free(*L);
(*L) = NULL;
return OK;
}
//1.找到要删除的结点
while (i < index) {
temp = temp->next;
i++;
}
//2.给e赋值要删除结点的数据域
*e = temp->data;
//3.修改被删除结点的前驱结点的后继指针
temp->prior->next = temp->next;
//4.修改被删除结点的后继结点的前驱指针
temp->next->prior = temp->prior;
//5. 删除结点temp
free(temp);
return OK;
}