在开始介绍卷积神经网络之前,觉得有必要先说一说计算机是如何读解图像语义的。在计算机中是采用什么样数据结构来保存图像。只有理解这些内容我们还此基础上开始研究让给你计算机像人类一样读取图片语义来做一些计算机任务。
我在西瓜视频发布相关视频,账号 zidea 头像和一致,希望大家多多关注。
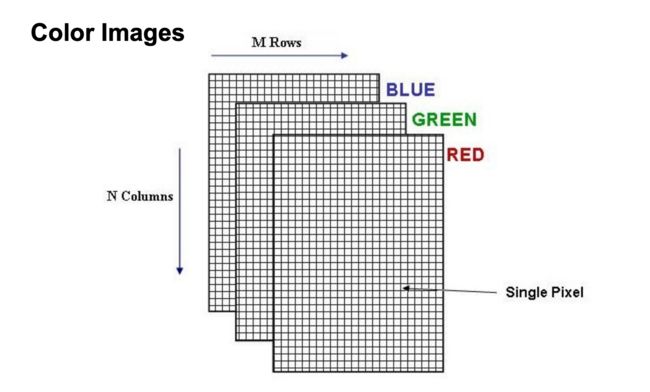
其实用矩阵来保存一张图像,通过将 3 维矩阵来表示一张图像,可以理解将图像切分一个一个小方块 (pixel) 每个小方块都有一个位置信息坐标,pixel 颜色通过 RBG 来表示,可能还具有透明通道,或者带有表示深度的通道,就用这些信息来表示一张图像输入给计算机。这样这种表示存储图像方式比较低级,会丢失许多语义信息。
我们可以将图像理解为一个函数 其中 和 表示像素位置,输出一个像素 RGB 值。
那么计算机在面对这些只有位置和颜色的信息数据,想要得到更多信息就需要靠自己,因为信息不足,这样对于计算机来理解或者读懂一张图片的语义无形带来困难。
以及有关图像的一些问题,我们需要读懂一张图像就像知道图像变化,计算机通过感知这些变化(边缘变化),有了边缘信息可以将图像进行分隔具有一定含义区域。
为了把握图片 intensity 变化看层空间上变换,空间变化程度可以看成图片的一些特征,在边和角是图片。
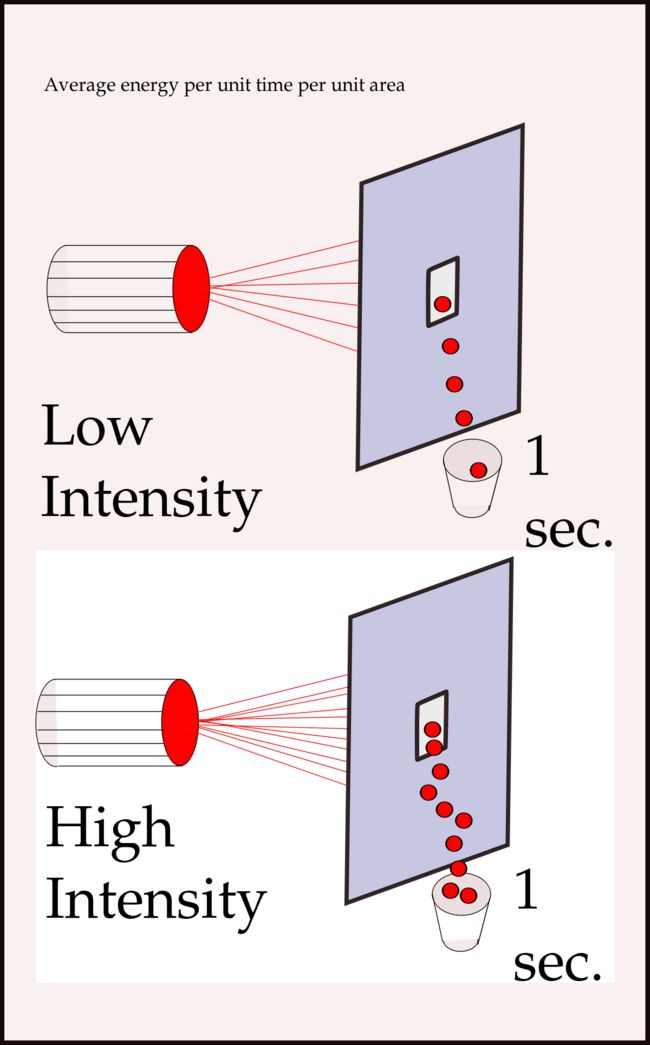
我们可以将图像处理为灰度图,在灰度图中明暗可以 intensity 来描述图片。这里 intensity 可以简单理解为我们某一像素(点)对光感知程度。怎么把这件事说清楚呢。我们看到物体是物体反射的光,发生不同颜色光以及光强度来反映一个物体。在计算机上我们将图像数字化过程,就是给图像每一个位置一个像素值,这个值可以分解为多个通道,值大小表示感光的程度。这就是我们在计算机视觉中要研究的对象。
通过 3D 视图形象地将我们如何通过灰度图 intensity 来表示图。接下来说一说卷积,
卷积
学习卷积神经也有一段时间,虽然已经了解到了如何将卷积应用到图像进行运算来得到特征图,以及卷积如何应用图片上进行滤波、降噪、锐化以及边缘检测。但是如何要深究卷积,还是有点摸不到头脑。所以收集一些资料。
我们先把公式抛出来,大家先看一看,觉得有点陌生也不要紧,接下来我们就来详细解释这个公式由来以及其应用
- 是在 上可以积分的函数
- 大家可能已经注意到了
- 所谓积分就是曲线进行切分很小的间隔然后进行求和,其实所谓的积分就是求和
- 假设两次抽取扑克牌概率是独立
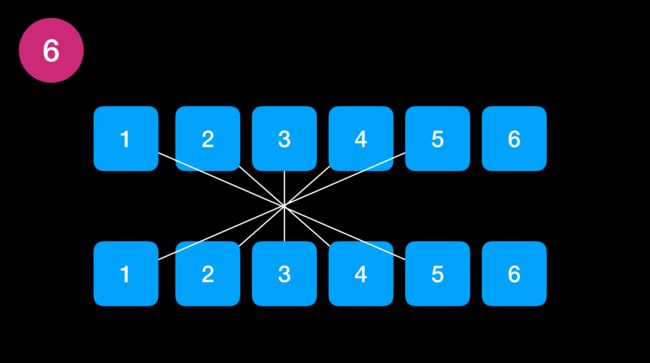
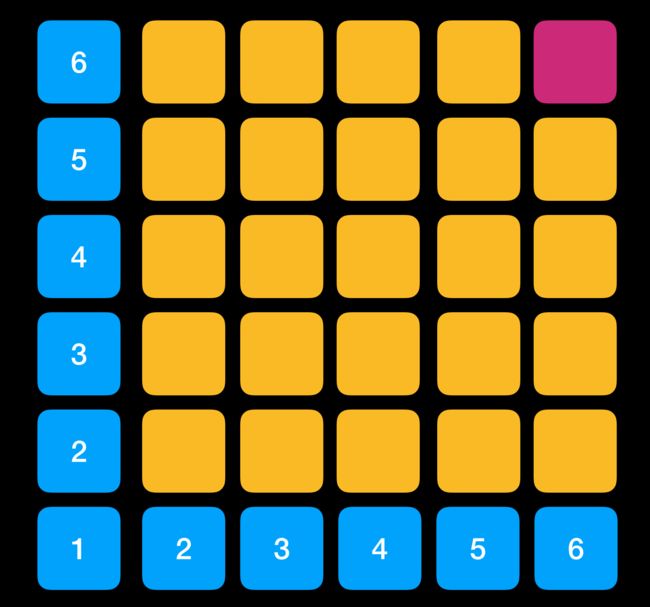
接下来用图解方式给大家详细介绍卷积,以及卷积的过程,假设我们有两个骰子,每次一起投掷骰子。通过连线来表示两两组合。
如果我们找出两个骰子数加起来为 6 的组合,通过连线方式表达出来
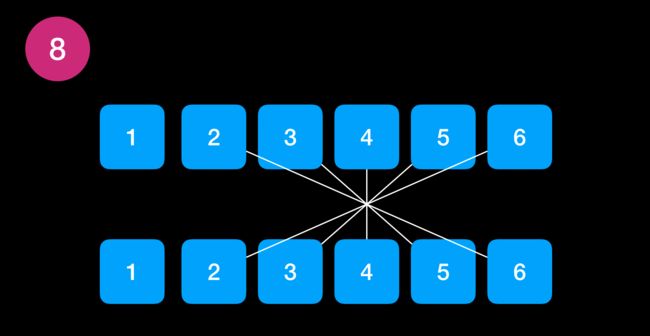
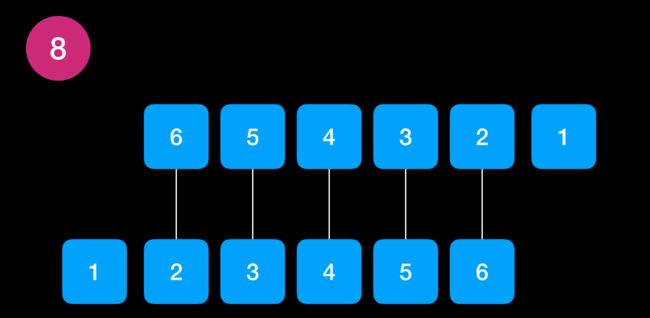
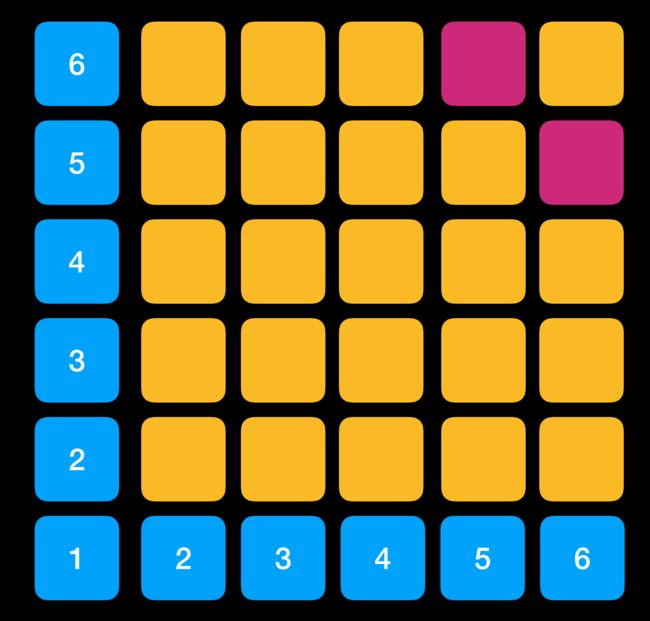
同上,如果我们想要找出两个骰子数加起来为 8 的组合,通过连线方式表达出来。不过这样连线看起来不是很舒服,所以我们可以通过翻卷得到就得到下面的形式,这就是卷积的由来。
这张图
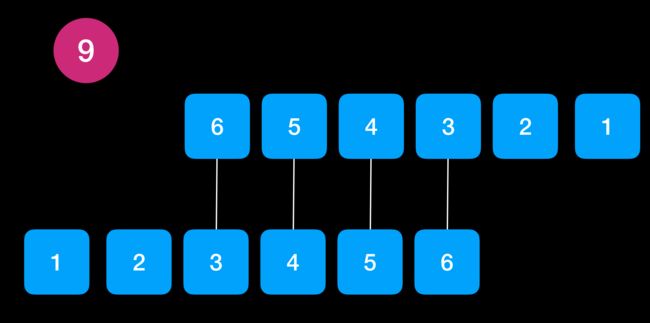
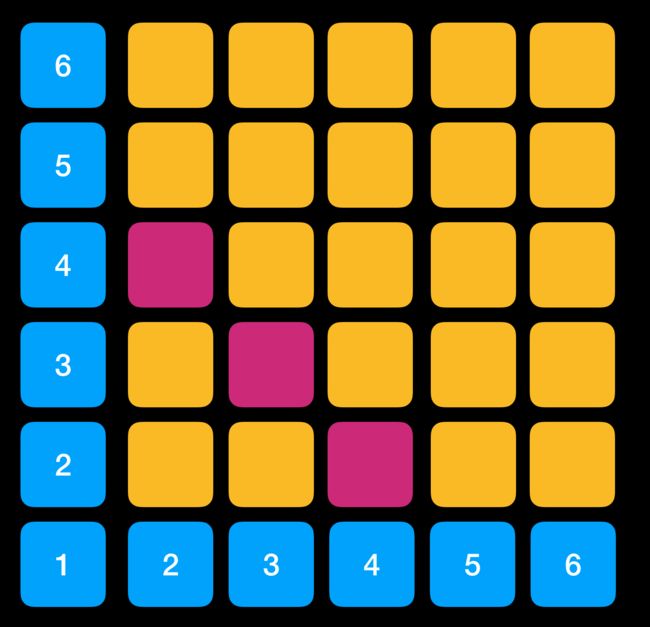
我们把一个骰子做行,另一个骰子作为列组成一个矩阵,如果再次选择让两个骰子数值相加得到某一个数值时,组合情况用颜色表示出来如以下几张图,就有点像将一张 paper 从右上角开始卷起。
卷积的特性
- 滤波Filtering
- 卷积Convolution
- 矩阵Matrix
- 颜色值Color values
- 卷积核 kernel:
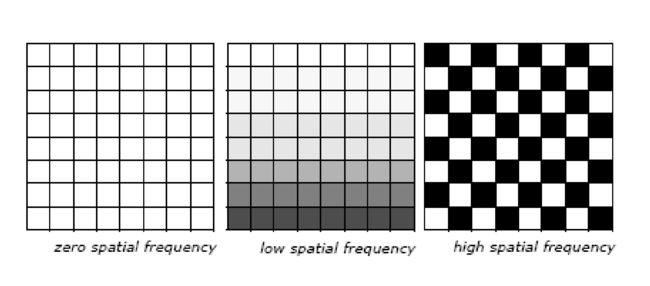
空间频率
卷积滤波用于修改图像的空间频率特性。
卷积的定义
- 一般卷积可以用于图片的滤镜效果,是对图像
- 卷积是运算,用整数组成的矩阵扫过图像
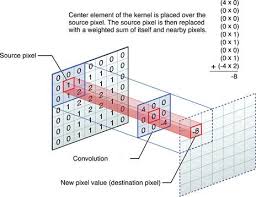
- 卷积在图片上作用可以看作,通过将所有相邻像素的加权值相加来确定中心像素的值
- 输出经过过滤的图像
- 卷积核就是放置权重的模版
卷积是如何处理图片
通过将一个像素及其相邻像素的颜色值乘以一个矩阵,也就是对应位置数值相乘。

- 卷积的像素
- 像素的值
- F 系数
- V 表示输出像素
卷积核进行旋转 180 度后,再去做卷积操作,如果不进行旋转卷积核的操作叫做相关,其实通常卷积核都是对称的。可以将我们神经网络学习到卷积核

卷积的性质
- 叠加性:
- 平移不变性:
- 交换律
- 结合律
- 分配律
- 标量
边界填充
一般经过卷积操作的图像会变小,所以为了保持输入和输出图像一样大小,需要在做卷积前对边界进行填充。
- 拉伸填充
- 镜像填充
- 0 填充
平滑和锐化

纹理特征(Texture Features)
形态特征(Morphological Features)
图像平滑
根据某一个像素其周围值来重新计算得到改点的新的值从而实现平滑。