调参

参数更新

神经网络的学习目的是找到使损失函数尽可能小的参数,即解决一个最优化问题.但是由于神经网络参数空间过于复杂,很难通过数学式求解的方式解决这个最优化问题.

SGD

将参数的梯度作为线索,沿梯度的反方向更新参数,重复这个步骤多次从而靠近最优参数,这个方式称为随机梯度下降(SGD)

class SGD:
    def __init__(self, lr=0.01):
         self.lr = lr
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]
# 参数更新过程伪代码
network = neural network(...)
optimizer = SGD()
for i in range(10000):
    ...
    x_batch, t_batch = get_mini_batch(...) # mini-batch
    grads = network.gradient(x_batch, t_batch)
    params = network.params
    optimizer.update(params, grads)
    ...

SGD低效的原因:梯度的方向并不一定指向最小值的方向,更新参数寻找最优解的过程会变得非常"曲折"

Momentum

这里代表物理学上的速度,表示动量参数,越小阻力越大,学习率表示重力系数
这个算法可以理解成质点在有阻力的曲面上(阻力大小正比于速度大小)受到重力影响运动的过程.

class Momentum:
    def __init__(self, alpha=0.9, eta = 1e-2):
        self.alpha = alpha
        self.eta = eta
        self.v = None
    def update(self, params, grads):
        if self.v is None: 
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
        for key in params.keys():
            self.v[key] = self.alpha * self.v[key] - self.eta * grads[key]
            params[key] += self.v[key]

AdaGrad

(Ada表示Adaptive)
AdaGrad方法是一种学习率衰减(learning rate decay)方法,随着学习的进行,学习率会逐渐减小,而AdaGrad则进一步发展了这种思想,参数空间的不同维度使用递减速度不同的学习率.

class AdaGrad:
     def __init__(self, lr= 1e-2):
        self.lr = lr,
        self.h = None
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key,val in params.items():
                self.h[key] = np.zeros_like(params[key])
        epsilon = 1e-7
        for key in params.items():
            self.h[key] += grads[key] * grads[key]
            params[key] += - self.lr  * grads[key] / (np.sqrt(self.h[key]) +epsilon)

Adam

Adam是一种结合了AdaGrad和Momentum的学习方法.

class Adam(GradientDescent):
    epsilon = 1e-7

    def __init__(self, lr=1e-3, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.m = None
        self.v = None
        self.iter = 0

    def update(self, grads, params):
        if self.m is None or self.v is None:
            self.m = {}
            self.v = {}
            for key, value in params.items():
                self.m[key] = np.zeros_like(value,dtype='float')
                self.v[key] = np.zeros_like(value,dtype='float')
        self.iter += 1
        lr_t = self.lr * np.sqrt(1. - self.beta2 ** self.iter) / (1. - self.beta1 ** self.iter)
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] * grads[key] - self.v[key])
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key] + self.epsilon))

初始值的选择

当激活函数使用ReLU函数时,权重初始函数使用He初始值,当激活函数为sigmoid或者tanh等S型函数时,初始值使用Xavier初始值.
He初始值: 标准差为的高斯分布,其中n为上一层节点数
Xavier初始值:标准差为的高斯分布,其中n为上一层节点数

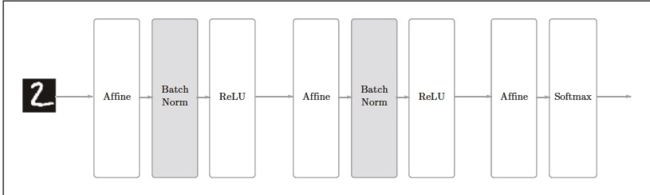
Batch Normalization(批标准化)

含有Batch Normalization层的神经网络

正向传播

反向传播