对局部性原理的一点理解
一个编写良好的计算机程序常常具有良好的局部性。也就是说。它们倾向于引用临近于其他最近引用过的数据项的数据项,或者最近引用过的数据项本身。这汇总倾向性,就被称为局部性原理,这是一个持久的概念,对硬件和软件系统的设计和性能都有着极大的影响。
局部性通常有两种不同的形式:时间局部性和空间局部性。在一个具有良好时间局部性的程序中,被引用一次的存储器位置很有可能在接下来时间内再被多次引用。在已给具有良好空间局部性的程序中,若一个存储器位置被引用了一次,那么在接下来时间内将引用附近的一个存储器位置。
一般而言,优良好局部性的程序比局部性差的程序运行的更快。现代计算机系统的各个层次,从硬件到OS、再到应用程序,它们的设计都利用了局部性。在硬件层,cache的引入就是利用了局部性,将最近被引用的指令和数据项存在cache中,从而提高了对主存的访问速度。在OS级,局部性原理允许使用主存作为虚拟地址空间作为最近被引用块的高速缓存;类似的使用主存来缓存磁盘文件系统中最近被使用磁盘快。在应用程序设计中,Web浏览器将最近被引用的文件放在本地磁盘中,就是利用的时间局部性。
下面是一个简单的函数:
int sum1(int v[])
{
int i, sum = 0;
int length = sizeof(v);
for(i = 0; i < length; i++)
sum += v[i];
return sum;
}该函数中,变量sum在每次循环迭代时被引用一次,因此对sum来说,有好的时间局部性。对变量v来说,它是一个int类型数组,循环时按顺序访问v[i],因而有很好的空间局部性,但时间局部性不好,因为每个元素只被访问了一次。这就有点像一个程序的时间复杂度和空间复杂度一样,二者是不可兼得的,所以只要满足时间和空间局部性二者之一,就可以说符合程序的局部性原则。
像上面这样顺序访问一个数组中的每个元素,称为具有*步长为1的的引用模式*,有时称该模式为顺序引用模式。一个连续数组中,每隔k个元素进行访问,称为*步长为k的引用模式*,一般来说,随着步长增加,空间局部性下降。
之前有一篇写展开循环的,通过减少循环的次数来节省运行时间。
http://blog.csdn.net/sinat_31508159/article/details/50541726
虽然说展开循环增加了步长,使空间局部性变差,但同时也减少了运行时间,所以说这是维持程序性能的一个折中选择。
下面是一个读取二位数组的例子:
int sum2(int array[][])//假设是一个 M*N 的二维数组
{
int i, j, sum = 0;
for(i = 0; i < M; i++)
{
for(j = 0; j < N; j++)
sum += array[i][j];
}
return sum;
}该函数对一个二维数组求和,双重嵌套循环按照行有限顺序读取数组中的元素。该函数有很好的空间局部性,因为它按照数组被存储的的行优先顺序来访问数组。
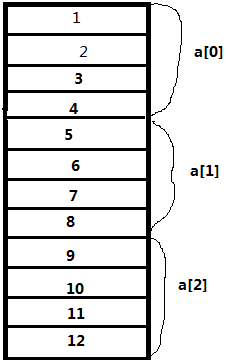
一个数组a[3][4]存储着1~12。虽然数组是二维的,但仍然是按照顺序存储在存储器中的。按行优先顺序读取该数组时,读出数据为1,2,3,4……11, 12,数据对应的存储位置分别为0, 1, 2, 3…… 恰好相当于读取一个顺序文件,这样有良好的空间局部性。
有时一些很小的改动会对程序产生很大的影响。下面的代码仅仅将行优先改为列优先:
int sum2(int array[][])//假设是一个 M*N 的二位数组
{
int i, j, sum = 0;
for(j = 0; i < M; i++)
{
for(i = 0; j < N; j++)
sum += array[i][j];
}
return sum;
}以列优先读取时,顺序是这样的:1, 5, 9, 2, 6, 10……8, 12
对应存储位置分别为:0, 4, 8, 1, 5, 9…… 7, 11
这个小改动不会改变程序的运行结果,但是改为列优先后,函数sum1按列顺序遍历数组,这样一来,相当于由步长为k = 1的引用模式变成了步长为k = 4的引用模式,导致空间局部性变差。
原因:是C数组在存储器中是按行顺序来存放的。
小结:
- 重复引用同一个变量的程序有良好的时间局部性。
- 对于具有步长为k的引用模式的程序来说,步长k越小,空间局部性越好。步长为1的程序有很好的空间局部性。以上面按列读取数组为例,在存储器以大步长跳来跳去的程序空间局部性会很差。
- 对于取指令来说,循环有很好的时间和空间局部性。循环体越小,循环迭代次数越多,局部性越好。
小结引自CSAPP第六章6.2.3局部性小结