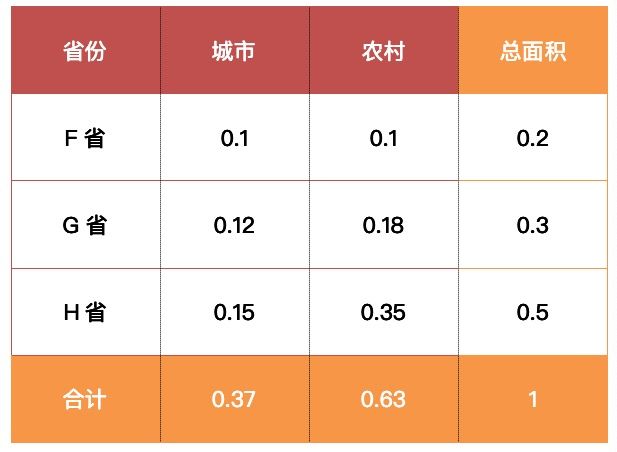
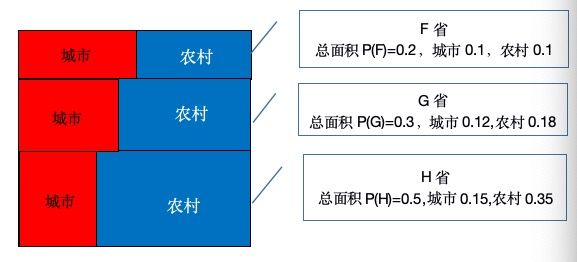
我们来看一个例子,一个国家有三个省份,分别是F省,G省和H省,三个省份的土地面积分布是P(F),P(G)和P(H),每个省份分为城市和农村两个部分,现在国家派下调研员,调研这三个省份的城市化情况,他得到了关于三个省份城市农村数据表格(见表1),并根据表格画出了更形象的占比图(见图1)
调研员要计算城市化指标出来,以便评比三个省份的城市化率情况,他利用符号P(城市|省份)记录该省份的城市面积占比,等于城市面积P(省份,城市)除以省份面积P(省份),例如关于F省份的城市占比计算公式如下:
P(城市|F)=P(F,城市)/P(F)=50%
同理G省和H省的城市占比计算公式分别为:
P(城市|G)=P(G,城市)/P(G)=40%
P(城市|H)=P(H,城市)/P(H)=30%
调研员通过计算,得到城市化率排序为F省>G省>H省。这个时候,H省份觉得这种评比方式不合理,他把调研员的符号做了一下改变,把"|"符号两边调换了一下,即由P(城市|省份)更改为P(省份|城市),调研员问,这符号表示什么,H省的工作人员答复说,这表示在所有的城市中,某个省份的城市占比,计算公式为P(省份,城市)/P(城市)。三个省份的计算公式如下:
P(F|城市)=P(F,城市)/P(城市)≈27%
P(G|城市)=P(G,城市)/P(城市)≈32%
P(H|城市)=P(H,城市)/P(城市)≈41%
调研员使用H省工作人员推荐的公式一算,发现在这个指标下,H省排在了最前头。
为何只是调换一下,意思完全不同,而且结果也很大的不同?
我们来看一下调研员使用的记号P(城市|F),这表示F省份的城市占比,是F省份的城市占F省总面积的比例。城市可以是H省的城市,也可以是G省的城市,但是设定了F省份作为一个前提条件,那么只能用F省的城市做计算。这其实就是条件概率,条件概率是指事件A在另外一个事件B已经发生条件下的发生概率,换句话说,事件A发生的概率要考虑事件B的影响。我们再看看H省推荐的符号P(F|城市),前提条件变为了城市,即三个省份的城市面积之和,在这个前提条件下来讨论F省份城市占城市总面积之比。
为什么调换一下,结果完全不同,那是因为在不同条件下计算概率导致的,条件不同,概率值当然也不同。这在日常生活中能找到各种例子,例如我们都知道经济好坏对股市的影响很大,经济好的时候(股市上涨的概率和经济差的时候股市上涨的概率是不同的。有句话说,抛开剂量谈毒性也有条件概率的意思在里面,剂量是一个前提条件,必须得考虑前提条件才能谈毒性大小。
根据以上的例子,可以更抽象提出条件概率的严格定义:
定义:如果A和B是两个事件,且P(B)≠0。那么事件B条件下,事件A的条件概率为
P(A|B)=P(A∩B)/P(B)
P(A∩B)表示A和B的交集,相当于双方的共同部分,在上例中,因为城市的面积包含在省份面积中,因此P(A∩B)就是城市的面积,其他P(A|B)和P(B)分别表示城市面积占比和省份面积。得到条件概率的公式,那就可以在公式上做做文章做更多的推论。
例如在公式两边都乘以P(B),得到推论1:
P(A∩B)=P(A|B)P(B)
左边P(A∩B)是城市的面积,右边P(A|B)城市面积占比,P(B)省份面积。还可以通过另一个例子来理解,例如专家预测经济上行的概率为P(经济上行),专家根据往年的统计,在经济上行的时候,股市上涨的概率为P(股市涨|经济上行),套用公式,我们可以推出经济上行而且股市涨的概率
P(股市涨∩经济上行)=P(股市涨|经济上行)×P(经济上行)
还有一个推论,我们知道,所有城市总面积是三个城市面积之和,计算公式如下:
P(城市)=P(F,城市)+P(G,城市)+P(H,城市)
我们再把推论1计算城市面积的公式套进去,得到:
P(城市)=P(城市|F)P(F)+P(城市|G)P(G)+P(城市|H)P(H)
这是通过已知的条件概率,来计算一个事件的概率的方法,这个推论是有前提条件的,只是在本例中这个前提条件看起来不那么明显,这个前提条件是三个省份不相关,或者互斥的,如果满足这个条件,我们可以得到更一般的推论公式:
推论2:有事件B1,B2,...,Bn,如果(这表示所有事件B并起来等于整个样本空间,例如三个省份面积并起来等于这个国家的面积),并且两个不同事件互斥(Bi∩Bj=Φ, 如果i≠j,对应到例子中,各个省份没有交集),且任意P(Bi)>0。那么,对于任意事件A,有:
P(A)=