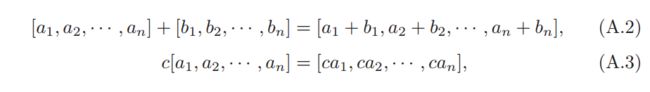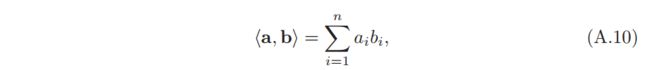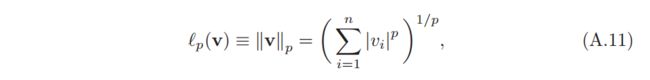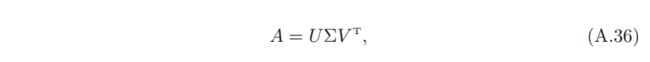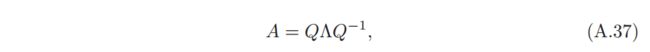github开源:https://nndl.github.io/
nndl作者:邱锡鹏
笔记作者:Isaac.(原创)
本书其他章节的笔记目录
线性代数主要包含向量、向量空间(或称线性空间)以及向量的线性变换和有限维的线性方程组。
目录结构
A.1 向量和向量空间
A.1.1 向量
A.1.2 向量空间
A.1.3 范数
A.1.4 常见的向量
A.2 矩阵
A.2.1 线性映射
A.2.2 矩阵操作
A.2.3 矩阵类型
A.2.4 特征值与特征向量
[图片上传中...(1566052999321.png-7d079c-1566055716718-0)]
A.2.5 矩阵分解
A.1 向量和向量空间
A.1.1 向量
标量(Scalar)是一个实数,只有大小,没有方向。
向量(Vector)是由一组实数组成的有序数组,同时具有大小和方向。
A.1.2 向量空间
向量空间(Vector Space),也称线性空间(Linear Space),是指由向量组成的集合, 并满足向量加法和标量乘法 。
欧氏空间(Euclidean Space):一个常用的线性空间。
线性子空间:向量空间 V 的线性子空间 U 是 V 的一个子集,并且满足向量空间的条件(向量加法和标量乘法)。
线性无关:线性空间 V 中的一组向量 { v1, v2, · · · , vn },如果对任意的一组标量 λ1, λ2, · · · , λn,满足 λ1v1 + λ2v2 + · · · + λnvn = 0,则必然 λ1 = λ2 = · · · =λn = 0,那么{ v1, v2, · · · , vn }是线性无关的。
基向量(Base Vector) 、坐标(Coordinates)
标准基(Standard Basis) 、笛卡尔坐标(Cartesian Coordinate)
内积:一个 n维线性空间中的两个向量 a 和 b,其内积为
正交:如果向量空间中两个向量的内积为 0,则它们正交(Orthogonal)。
A.1.3 范数
范数(Norm)是一个表示向量“长度”的函数。
一个常见的范数函数为 ℓp 范数
ℓ1 范数为向量的各个元素的绝对值之和。
ℓ2 范数为向量的各个元素的平方和再开平方,也常称为向量的模。
ℓ∞ 范数为向量的各个元素的最大绝对值 。
A.1.4 常见的向量
one-hot向量为有且只有一个元素为 1,其余元素都为 0 的向量。
A.2 矩阵
A.2.1 线性映射
线性映射(Linear Mapping) 、矩阵(Matrix) 、列向量 、行向量
A.2.2 矩阵操作
矩阵相加:两个矩阵大小必须相同。
矩阵乘积:两个矩阵的乘积仅当第一个矩阵的列数和第二个矩阵的行数相等时才能定义。
Hadamard 积 :A和 B 的Hadamard 积,也称为逐点乘积,为 A和 B 中对应的元素相乘。
转置(Transposition):行列对调。
向量化:矩阵的向量化是将矩阵表示为一个列向量。
迹(Trace):方块矩阵 A的对角线元素之和,tr(AB) = tr(BA) 。
行列式:det(A)或 |A| 。
秩(Rank):一个矩阵 A 的列秩是 A 的线性无关的列向量数量,行秩是 A 的线性无关的行向量数量。一个矩阵的列秩和行秩总是相等的。
一个 m × n 的矩阵 A 的秩最大为 min(m, n) 。若 rank(A) = min(m, n),则称矩阵为满秩的。
如果一个矩阵不满秩,说明其包含线性相关的列向量或行向量,其行列式为 0 。
两个矩阵的乘积 AB 的秩 rank(AB) ≤ min(rank(A), rank(B))。
A.2.3 矩阵类型
对称矩阵(Symmetric Matrix):指其转置等于自己的矩阵,A = AT 。
对角矩阵(Diagonal Matrix):是一个主对角线之外的元素皆为 0 的矩阵。对角矩阵 A也可以记为 diag(a)。
单位矩阵(Identity Matrix):In 是一种特殊的的对角矩阵,其主对角线元素为 1,其余元素为 0。 一个矩阵和单位矩阵的乘积等于其本身。
逆矩阵(Inverse Matrix) :AB = BA = In。其中 In 为单位阵,则称 A 是可逆的。矩阵 B 称为矩阵 A 的逆矩阵,记为 A-1 。 一个方阵的行列式等于 0 当且仅当该方阵不可逆。
正定矩阵(Positive-Definite Matrix):对于一个 n × n 的对称矩阵 A,如果对于所有的非零向量 x ∈ Rn 都满足 xTAx > 0,则A为正定矩阵。若xTAx ≥ 0则A是半正定矩阵(Positive-Semidefinite Matrix)。
正交矩阵(Orthogonal Matrix ):A 为方块矩阵,其逆矩阵等于转置矩阵。
AT = A-1,即 ATA = AAT = In。
A.2.4 特征值与特征向量
对一个矩阵 A,如果存在一个标量 λ 和一个非零向量 v 满足 Av = λv 则 λ 和 v 分别称为矩阵 A 的特征值(Eigenvalue)和特征向量(Eigenvector)。
A.2.5 矩阵分解
一个矩阵通常可以用一些比较“简单”的矩阵来表示,称为矩阵分解(Matrix Decomposition, Matrix Factorization)。
奇异值分解(Singular Value Decomposition, SVD) :m × n 的矩阵 A
其中 U 和 V 分别为 m × m 和 n × n 的正交矩阵,、Σ 为 m × n 的对角矩阵,其对角线上的元素称为奇异值。
特征分解 (Eigendecomposition):一个n × n 的方块矩阵 A
其中 Q 为 n × n 的方块矩阵,其每一列都为A的特征向量,Λ 为对角阵,其每一个对角元素为的特征值。
如果 A 为对称矩阵,则 A 可以被分解为
其中 Q 为正交阵。
本书其他章节的笔记目录