#include
#include
#include
//双亲表示法
#define MAX_TREE_SIZE 10
#define OK 1
#define ERROR 0
#define true 1
#define false 0
#define EOVERFLOW 0
typedef char ElemType;
typedef int bool;
typedef int Status;
enum TREEWAY
{
PREORDER, INORDER, POSTORDER, LEVEL
};
enum TREEWAY treeWay = PREORDER;
char blankStr=' ';//空格
typedef struct _BTNode{
ElemType data;
struct _BTNode *lchild,*rchild;
}BiTNode,*BiTree;
//---------------栈(链表)相关开始----------------------
typedef BiTree SElemType;
typedef struct _SqNode{
SElemType data;
struct _SqNode *next;
}SqNode;
typedef struct _SqStack{
SqNode *top;
int count;//栈计数器
}SqStack;
void Init_Stack(SqStack *stack){
stack->top=NULL;
stack->count=0;
}
//压栈
Status Push(SqStack *stack,SElemType e){
SqNode *node=NULL;
do{
node=(SqNode*)malloc(sizeof(SqNode));
}while(!node);
node->data=e;
node->next=stack->top;
stack->top=node;
stack->count++;
return OK;
}
//出栈 后进先出
Status Pop(SqStack *stack,SElemType *e){
if(stack->top){
SqNode *tmp=stack->top;
stack->top=tmp->next;
*e=tmp->data;
free(tmp);
stack->count--;
return OK;
}else{
printf("栈为空,出栈失败\n");
return ERROR;
}
}
void Clear_Stack(SqStack *stack){
if(!stack->top)return;
SqNode *p=stack->top;
SqNode *tmp;
while(p){
tmp=p;
p=tmp->next;
free(tmp);
}
stack->top=NULL;
stack->count=0;
}
void Destory_Stack(SqStack *stack){
Clear_Stack(stack);
free(stack);
}
int Stack_IsEmpty(SqStack stack){
if(stack.top){
return false;
}
return true;
}
//---------------栈相关结束----------------------
//---------------队列(顺序结构,循环)相关开始----------------------
const int INIT_QUEUE_SIZE=100;
const int INCREAMENT_QUEUE_SIZE=2;
typedef BiTree QElemType;
typedef struct _SqQueue{
int front;//对头
int rear;//对尾
QElemType *base;
int size;
int capacity;
}Queue;
Queue* Init_Queue(){
Queue* q=(Queue*)malloc(sizeof(Queue));
if(!q){
return NULL;
}
q->base=(QElemType*)malloc(sizeof(QElemType)*INIT_QUEUE_SIZE);
q->front=q->rear=0;
q->size=0;
q->capacity=INIT_QUEUE_SIZE;
return q;
}
int Queue_IsFull(Queue *q){
if(q->size==q->capacity){
return true;
}
return false;
}
int Queue_IsEmpty(Queue *q){
if(q->size==0){
return true;
}
return false;
}
void Clear_Queue(Queue *queue){
queue->front=queue->rear=0;
queue->size=0;
}
void Destroy_Queue(Queue *queue){
free(queue->base);
queue->base=NULL;
}
//扩容 未完善
Queue* Copy_Queue(Queue *q){
if(q->base==NULL){
return q;
}
Queue* newQueue=(Queue*)malloc(sizeof(Queue));
newQueue->base=(QElemType*)malloc(sizeof(QElemType)*(q->capacity+INCREAMENT_QUEUE_SIZE));
newQueue->front=newQueue->rear=0;
newQueue->size=0;
newQueue->capacity=q->capacity+INCREAMENT_QUEUE_SIZE;
int i,end,index=0;
//队尾与对头相减大于0 则最大下标为队尾,否则下标为队列最大容量 可能存在重头开始情况
bool flag=q->rear-q->front>0;
if(flag){
end=q->rear;
}else{
end=q->capacity;
}
for(i=q->front;ibase[index++]=q->base[i];
}
if(!flag){
for(int j=0;jrear;j++){
newQueue->base[index++]=q->base[j];
}
}
newQueue->size=q->size;
return newQueue;
}
//入队列
void Push_Queue(Queue *q,QElemType e){
//判断队列容量是否已经满了 重新分配
if(Queue_IsFull(q)){
printf("\n队列已满,无法入队\n");
return ;
}
//将新元素赋值到队尾
q->base[q->rear]=e;
//重新设置队尾
//获取下一个下标,取模 循环当下标到最大时,从0开始;
int nextIndex=(q->rear+1)%(q->capacity);
q->rear=nextIndex;
q->size++;
}
void Pop_Queue(Queue *q,QElemType *e){
//判断是否为空
if(q->size==0){
printf("队列为空,不能出队\n");
return;
}
*e=q->base[q->front];
int nexIndex=(q->front+1)%q->capacity;
q->front=nexIndex;
q->size--;
}
//---------------队列相关结束----------------------
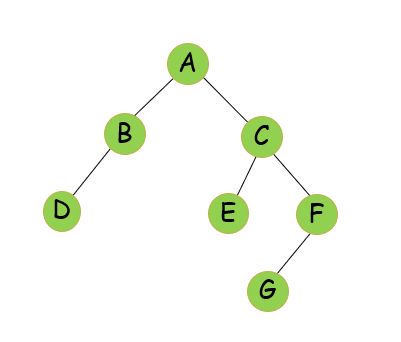
//创建二叉树
void CreateBiTree(BiTree *Root){
ElemType val=0;
val=getchar();
//如果输入' ',则指向为空
if(val == blankStr){
(*Root) = NULL;
//如果输入非' ',则给数据域赋值
}else{
*Root = (BiTNode*)malloc(sizeof(BiTNode));//根节点
if(!(*Root)){
printf("创建节点失败,无法分配可用内存...");
exit(EOVERFLOW);
}else{
(*Root)->data=val;
//创建左子树
CreateBiTree(&(*Root)->lchild);//左节点
//创建右子树
CreateBiTree(&(*Root)->rchild);//右节点
}
}
}
//判断二叉树是否为空
int BiTreeEmpty(BiTree T){
if(T){
return false;
}
return true;
}
int BiTreeDepth(BiTree T){
if(!T){
return 0;
}
//树的高度 = max(左子树的高度,右子树的高度) + 1
int leftDepth = BiTreeDepth(T->lchild);
int rightDepth = BiTreeDepth(T->rchild);
return leftDepth >= rightDepth ? leftDepth + 1 : rightDepth + 1;
}
//获取树的叶子节点个数
int getLeafNum(BiTree T){
if(!T){
return 0;
}
if(!T->lchild && !T->rchild){
return 1;
}
int num=0;
num+=getLeafNum(T->lchild);
num+=getLeafNum(T->rchild);
return num;
}
//打印所有叶子节点
void printLeaf(BiTree T){
if(!T)return;
//叶子节点 打印
if(!T->lchild && !T->rchild){
putchar(T->data);
return;
}
printLeaf(T->lchild);
printLeaf(T->rchild);
}
void Traverse(BiTree T,enum TREEWAY treeWay){
if(T){
//前序遍历
//访问根结点 (V);
//前序遍历左子树 (L);
//前序遍历右子树 (R)
if(treeWay==PREORDER){
putchar(T->data);
Traverse(T->lchild,treeWay);
Traverse(T->rchild,treeWay);
//中序遍历
//前序遍历左子树 (L);
//访问根结点 (V);
//前序遍历右子树 (R)
}else if(treeWay==INORDER){
Traverse(T->lchild,treeWay);
putchar(T->data);
Traverse(T->rchild,treeWay);
//后序遍历
//前序遍历左子树 (L);
//访问根结点 (V);
//前序遍历右子树 (R)
}else if(treeWay==POSTORDER){
Traverse(T->lchild,treeWay);
Traverse(T->rchild,treeWay);
putchar(T->data);
//层序遍历:
//从树的第一层开始,从上而下逐层遍历,在同一层中,按从左到右顺序逐个访问;
}else if(treeWay==LEVEL){
//关键中间变量存放每一层的数据
BiTree temp[100];
int in=0,out =0;
temp[in++]=T;
//每次把这一层存入,然后输出的时候就把他的左右节点存入
//例如一颗完全二叉树abcdefg 输出a的时候把bc放入,输出b的时候把b的孩子放入也就是de,再输出c并且放入孩子fg,依次这样,达到层序的要求
while(in>out){
if(temp[out]){
putchar(temp[out]->data);
temp[in++]=temp[out]->lchild;
temp[in++]=temp[out]->rchild;
}
out++;
}
}
}
}
//以递归形式先序遍历二叉树
void PreOrderTraverse(BiTree T){
Traverse(T,PREORDER);
}
//以递归形式中序遍历二叉树
void InOrderTraverse(BiTree T){
Traverse(T,INORDER);
}
//以递归形式后序遍历二叉树
void PostOrderTraverse(BiTree T){
Traverse(T,POSTORDER);
}
void LevelTraverse1(BiTree T){
Traverse(T,LEVEL);
}
//层序遍历
void LevelTraverse(BiTree T){
if(T){
Queue *queue=Init_Queue();
//根节点入队
Push_Queue(queue,T);
BiTree tmp;
while(!Queue_IsEmpty(queue)){
Pop_Queue(queue,&tmp);
putchar(tmp->data);
if(tmp->lchild){
Push_Queue(queue,tmp->lchild);
}
if(tmp->rchild){
Push_Queue(queue,tmp->rchild);
}
}
}
}
//前序非递归遍历
void NoPreOrderTraverse(BiTree T){
if(!T){
fprintf(stdout, "树为空\n");
return;
}
SqStack stack;//栈记录遍历过的左子树
Init_Stack(&stack);
BiTree tmp= T;
while(tmp || !Stack_IsEmpty(stack)){
//将tmp节点的左子树全部压入栈并打印,
while(tmp){
Push(&stack,tmp);
putchar(tmp->data);
tmp=tmp->lchild;
}
//到叶子结点后,出栈,获取右子树
if(!Stack_IsEmpty(stack)){
Pop(&stack, &tmp);
//将 tmp 置为右节点
tmp = tmp->rchild;
}
//继续循环 压入右子树的左子树。
}
}
//中序非递归遍历
void NoInOrderTraverse(BiTree T){
if(!T){
fprintf(stdout, "树为空\n");
return;
}
SqStack stack;
Init_Stack(&stack);
BiTree tmp= T;
while(tmp || !Stack_IsEmpty(stack)){
//将tmp节点的左子树压入栈
while(tmp){
Push(&stack,tmp);
tmp=tmp->lchild;
}
//到叶子结点后,出栈,访问该栈顶结点并打印, 获取右子树
if(!Stack_IsEmpty(stack)){
Pop(&stack, &tmp);
putchar(tmp->data);
//将 tmp 置为右节点
tmp = tmp->rchild;
}
//继续循环 压入右子树的左子树。
}
}
//后序非递归遍历
//后序遍历中,要保证左孩子和右孩子都已被访问,并且左孩子在右孩子之前访问才能访问根结点
void NoPostOrderTraverse(BiTree T){
if(!T){
fprintf(stdout, "树为空\n");
return;
}
SqStack stack;
Init_Stack(&stack);
BiTree cur;//当前节点
BiTree pre=NULL;//前一次访问的结点
BiTree tmp;
//将根节点入栈
Push(&stack, T);
while(!Stack_IsEmpty(stack)){
//获取当前节点
cur=stack.top->data;
//如果当前节点不存在左孩子和右孩子(相对的根节点),则可以直接访问它
//或者 当前节点存在左孩子或右孩子,但是其左孩子和右孩子都已经被访问过 则可以直接访问它
if((!cur->lchild && !cur->rchild)||(pre && (pre==cur->lchild||pre==cur->rchild))){
putchar(cur->data);//如果当前结点没有孩子结点或者孩子结点都已被访问过
Pop(&stack, &tmp);
pre = cur;
}else{
//将当前节点的右孩子和左孩子依次入栈,这样就保证了每次取栈顶元素的时候,左孩子在右孩子之前别访问,左孩子和右孩子都在根结点前面被访问
if(cur->rchild){
Push(&stack,cur->rchild);
}
if(cur->lchild){
Push(&stack,cur->lchild);
}
}
}
}
int main()
{
BiTree tree=NULL;
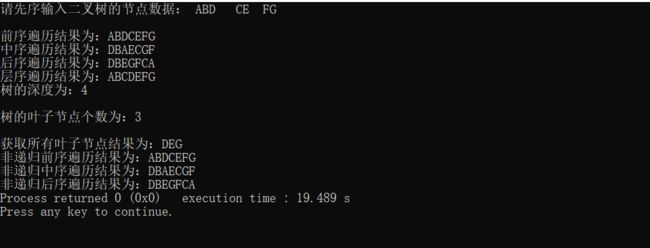
printf("请先序输入二叉树的节点数据: ");
CreateBiTree(&tree);
printf("\n前序遍历结果为:");
PreOrderTraverse(tree);
printf("\n中序遍历结果为:");
InOrderTraverse(tree);
printf("\n后序遍历结果为:");
PostOrderTraverse(tree);
printf("\n层序遍历结果为:");
LevelTraverse1(tree);
printf("\n树的深度为:%d\n",BiTreeDepth(tree));
printf("\n树的叶子节点个数为:%d\n",getLeafNum(tree));
printf("\n获取所有叶子节点结果为:");
printLeaf(tree);
printf("\n非递归前序遍历结果为:");
NoPreOrderTraverse(tree);
printf("\n非递归中序遍历结果为:");
NoInOrderTraverse(tree);
printf("\n非递归后序遍历结果为:");
NoPostOrderTraverse(tree);
return 0;
}
号为空格
ABD###CE##FG###