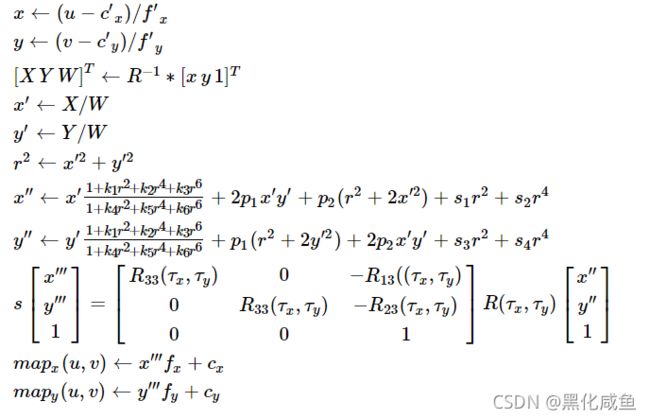单目相机标定结果的评估——重投影误差与畸变校正

目录

1.重投影误差的概念

2.基于摄像机模型的重投影误差

3.畸变校正算法

3.1利用畸变模型正向求解

3.2利用畸变模型反向求解

---

1.重投影误差的概念

在相机标定后，我们可以通过计算重投影误差来判断标定地精准程度。在标定后每个三维点根据相机的投影矩阵计算得到的图像位置与实际图像位置之间总存在一个距离，这个距离的累加和就是重投影误差。重投影误差不仅考虑的单应矩阵间的计算误差，也考虑了图像的测量误差，因此适合用来评价标定结果。重投影误差受镜头畸变等因素的影响，因此本文比较了畸变矫正前后的重投影误差大小。

2.基于摄像机模型的重投影误差

我们知道有限射影摄像机模型下，三维点X和图像点x之间的映射关系如下：

则计算得到的图像点位置可以用世界坐标系坐标表示为：

将求得的图像点与实际图像点间求二范数即反投影误差，各点反投影误差之和即重投影误差。笔者猜想，这就是OpenCV中调用projectPoints()函数时，令畸变系数为0时所采用的算法，笔者通过实验发现结果与猜想基本一致。

值得注意的是，这里没有考虑镜头的畸变。 

3.畸变校正算法

我们在相机标定结束后获得的五个畸变系数：k1,k2,k3,p1,p2分别代表了径向畸变和切向畸变的系数，公式如下：

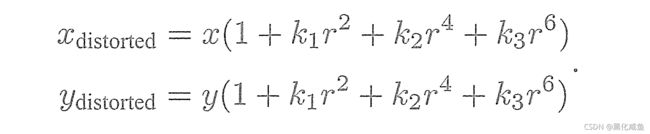径向畸变公式 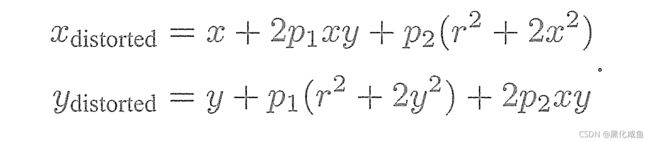切向畸变公式 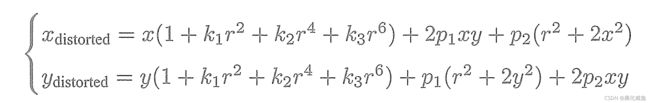综合径向畸变和切向畸变的公式

 注意，为理想坐标，为畸变后的坐标，且两个坐标均在归一化平面上。因此原始图像的已知坐标为，畸变矫正的过程就是根据原始图像计算理想坐标的过程。

 笔者在OpenCV官方文档上找到了使用该模型的矫正算法。

3.1利用畸变模型正向求解

OpenCV官方文档由理想坐标点到带畸变坐标点的正向求解的算法如下：

该算法的基本思路为：

理想图像坐标系,转移到相面坐标,再通过归一化，得到归一化平面上的坐标，利用畸变模型（图中的畸变参数暂未用到，默认为0）得到畸变后的坐标（如果是双目相机模型，还需要利用相机间的旋转矩阵，得到该点在某一相机相面上的图像位置）。再利用图像坐标系和相面坐标系的关系还原到图像系中，得到畸变后的，从而得到了畸变前后图像坐标系的映射关系，利用这种映射关系就能对图像进行矫正。

该算法的对应OpenCV函数为：initUndistortRectifyMap()，函数原型如下：

CV_EXPORTS_W
void initUndistortRectifyMap(
InputArray cameraMatrix, // computed camera matrix
InputArray distCoeffs,                  
InputArray R, 
InputArray newCameraMatrix,
Size size, 
int m1type, 
OutputArray map1, 
OutputArray map2);

得到映射后，调用remap()来矫正每幅图像。

CV_EXPORTS_W 
void remap( 
InputArray src, 
OutputArray dst,
InputArray map1, 
InputArray map2,
int interpolation, 
int borderMode = BORDER_CONSTANT,
const Scalar& borderValue = Scalar());

如果仅需要矫正一幅图像，可以将两个函数组合起来方便调用，OpenCV提供了这种函数undistort()，其函数原型如下：

CV_EXPORTS_W 
void undistort( 
InputArray src, 
OutputArray dst,
InputArray cameraMatrix,
InputArray distCoeffs,
InputArray newCameraMatrix = noArray() );

3.2利用畸变模型反向求解

OpenCV还提供了根据带畸变点坐标计算理想点坐标的算法。

注意，其中undistort()是一种近似的迭代算法，它从归一化的畸变点坐标中估计归一化的原始点坐标(“归一化”意味着坐标不依赖于相机矩阵)。

使用该算法对应的函数为undistortPoints()，函数原型如下：

CV_EXPORTS_W
void undistortPoints(
InputArray src, 
OutputArray dst,                
InputArray cameraMatrix, 
InputArray distCoeffs,
InputArray R = noArray(), 
InputArray P = noArray());