基于金枪鱼群优化算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、金枪鱼群优化算法
-
- (1)初始化
- (2)螺旋觅食
- (3)抛物线觅食
- 2、TSO算法伪代码
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
1、金枪鱼群优化算法
金枪鱼群优化(Tuna swarm optimization, TSO)算法的主要灵感来自金枪鱼群的合作觅食行为。该算法模拟了金枪鱼群体的两种觅食行为,即螺旋觅食和抛物线觅食。
(1)初始化
与大多数基于群体的元启发式算法类似,TSO通过在搜索空间中均匀随机生成初始种群来启动优化过程。 X i i n t = rand ⋅ ( u b − l b ) + l b , i = 1 , 2 , ⋯ , N P (1) \text{\bf X}_i^{\rm int}=\text{\bf rand}\cdot({\rm\bf ub-lb)+lb},\,\,i=1,2,\cdots,NP\tag{1} Xiint=rand⋅(ub−lb)+lb,i=1,2,⋯,NP(1)其中, X i i n t \text{\bf X}_i^{\rm int} Xiint是第 i i i个个体的初始位置, u b \rm\bf ub ub和 l b \rm\bf lb lb分别是搜索空间的上界和下界, N P NP NP是金枪鱼种群的数量, r a n d \rm\bf rand rand是一个均匀分布在 [ 0 , 1 ] [0,1] [0,1]内的随机向量。
(2)螺旋觅食
金枪鱼群通过形成紧密的螺旋来追逐猎物,除了追逐猎物,成群的金枪鱼还相互交换信息。每一条金枪鱼都跟在前一条鱼的后面,因此可以在相邻的金枪鱼之间共享信息。基于上述原理,螺旋觅食策略的数学公式如下: X i t + 1 = { α 1 ⋅ ( X b e s t t + β ⋅ ∣ X b e s t t − X i t ∣ ) + α 2 ⋅ X i t , i = 1 α 1 ⋅ ( X b e s t t + β ⋅ ∣ X b e s t t − X i t ∣ ) + α 2 ⋅ X i − 1 t , i = 2 , 3 , ⋯ , N P (2) \text{\bf X}_i^{t+1}=\begin{dcases}\alpha_1\cdot\left(X_{best}^t+\beta\cdot|X_{best}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_i^t,\quad\,\,\,\,\, i=1\\[2ex]\alpha_1\cdot\left(X_{best}^t+\beta\cdot|X_{best}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_{i-1}^t,\quad i=2,3,\cdots,NP\end{dcases}\tag{2} Xit+1=⎩⎨⎧α1⋅(Xbestt+β⋅∣Xbestt−Xit∣)+α2⋅Xit,i=1α1⋅(Xbestt+β⋅∣Xbestt−Xit∣)+α2⋅Xi−1t,i=2,3,⋯,NP(2) α 1 = a + ( 1 − a ) ⋅ t t max (3) \alpha_1=a+(1-a)\cdot\frac{t}{t_{\max}}\tag{3} α1=a+(1−a)⋅tmaxt(3) α 2 = ( 1 − a ) − ( 1 − a ) ⋅ t t max (4) \alpha_2=(1-a)-(1-a)\cdot\frac{t}{t_{\max}}\tag{4} α2=(1−a)−(1−a)⋅tmaxt(4) β = e b l ⋅ cos ( 2 π b ) (5) \beta=e^{bl}\cdot\cos(2\pi b)\tag{5} β=ebl⋅cos(2πb)(5) l = e 3 cos ( ( ( t max + 1 ) / t ) − 1 ) π ) (6) l=e^{3\cos(((t_{\max}+1)/t)-1)\pi)}\tag{6} l=e3cos(((tmax+1)/t)−1)π)(6)其中, X i t + 1 \text{\bf X}_i^{t+1} Xit+1是第 t + 1 t+1 t+1次迭代的第 i i i个个体, X b e s t t X_{best}^t Xbestt是当前最佳个体(食物), α 1 \alpha_1 α1和 α 2 \alpha_2 α2是控制个体向最佳个体和前一个个体移动趋势的权重系数, a a a是一个常数,用于确定金枪鱼在初始阶段跟随最佳个体和前一个体的程度, t t t表示当前迭代次数, t m a x t_{max} tmax表示最大迭代次数, b b b是均匀分布在0到1之间的随机数。
当最优个体找不到食物时,盲目跟随最优个体觅食不利于群体觅食。因此,考虑在搜索空间中生成一个随机坐标,作为螺旋搜索的参考点。它使每个个体都能在更广阔的空间里探索,并使TSO具有全局探索能力。具体的数学模型描述如下: X i t + 1 = { α 1 ⋅ ( X r a n d t + β ⋅ ∣ X r a n d t − X i t ∣ ) + α 2 ⋅ X i t , i = 1 α 1 ⋅ ( X r a n d t + β ⋅ ∣ X r a n d t − X i t ∣ ) + α 2 ⋅ X i − 1 t , i = 2 , 3 , ⋯ , N P (7) \text{\bf X}_i^{t+1}=\begin{dcases}\alpha_1\cdot\left(X_{rand}^t+\beta\cdot|X_{rand}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_i^t,\quad\,\,\,\,\, i=1\\[2ex]\alpha_1\cdot\left(X_{rand}^t+\beta\cdot|X_{rand}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_{i-1}^t,\quad i=2,3,\cdots,NP\end{dcases}\tag{7} Xit+1=⎩⎨⎧α1⋅(Xrandt+β⋅∣Xrandt−Xit∣)+α2⋅Xit,i=1α1⋅(Xrandt+β⋅∣Xrandt−Xit∣)+α2⋅Xi−1t,i=2,3,⋯,NP(7)其中, X r a n d t X_{rand}^t Xrandt是搜索空间中随机生成的参考点。
特别地,元启发式算法通常在早期阶段进行广泛的全局探索,然后逐渐过渡到精确的局部开发。因此,随着迭代次数的增加,TSO将螺旋觅食的参考点从随机个体更改为最优个体。综上所述,螺旋觅食策略的最终数学模型如下: X i t + 1 = { { α 1 ⋅ ( X r a n d t + β ⋅ ∣ X r a n d t − X i t ∣ ) + α 2 ⋅ X i t , i = 1 α 1 ⋅ ( X r a n d t + β ⋅ ∣ X r a n d t − X i t ∣ ) + α 2 ⋅ X i − 1 t , i = 2 , 3 , ⋯ , N P , if rand < t t max { α 1 ⋅ ( X b e s t t + β ⋅ ∣ X b e s t t − X i t ∣ ) + α 2 ⋅ X i t , i = 1 α 1 ⋅ ( X b e s t t + β ⋅ ∣ X b e s t t − X i t ∣ ) + α 2 ⋅ X i − 1 t , i = 2 , 3 , ⋯ , N P , if rand ≥ t t max (8) \text{\bf X}_i^{t+1}=\begin{cases}{\begin{cases}\alpha_1\cdot\left(X_{rand}^t+\beta\cdot|X_{rand}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_i^t,\quad\,\,\,\,\, i=1\\[2ex]\alpha_1\cdot\left(X_{rand}^t+\beta\cdot|X_{rand}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_{i-1}^t,\quad i=2,3,\cdots,NP\end{cases},\text{if}\,\,\text{rand}<\frac{t}{t_{\max}}}\\[2ex]\\{\begin{cases}\alpha_1\cdot\left(X_{best}^t+\beta\cdot|X_{best}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_i^t,\quad\,\,\,\,\, i=1\\[2ex]\alpha_1\cdot\left(X_{best}^t+\beta\cdot|X_{best}^t-\text{\bf X}_i^t|\right)+\alpha_2\cdot\text{\bf X}_{i-1}^t,\quad i=2,3,\cdots,NP\end{cases},\,\,\,\,\text{if}\,\,\text{rand}\geq \frac{t}{t_{\max}}}\end{cases}\tag{8} Xit+1=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎩⎨⎧α1⋅(Xrandt+β⋅∣Xrandt−Xit∣)+α2⋅Xit,i=1α1⋅(Xrandt+β⋅∣Xrandt−Xit∣)+α2⋅Xi−1t,i=2,3,⋯,NP,ifrand<tmaxt⎩⎨⎧α1⋅(Xbestt+β⋅∣Xbestt−Xit∣)+α2⋅Xit,i=1α1⋅(Xbestt+β⋅∣Xbestt−Xit∣)+α2⋅Xi−1t,i=2,3,⋯,NP,ifrand≥tmaxt(8)
(3)抛物线觅食
金枪鱼除了形成螺旋觅食外,还形成抛物线合作觅食。金枪鱼以食物为参照点形成抛物线形。此外,金枪鱼通过在周围搜索来寻找食物。假设两种方法的选择概率均为50%,则两种方法同时进行。具体的数学模型描述如下: X i t + 1 = { X b e s t t + r a n d ⋅ ( X b e s t t − X i t ) + T F ⋅ p 2 ⋅ ( X b e s t t − X i t ) , if rand < 0.5 T F ⋅ p 2 ⋅ X i t , if rand ≥ 0.5 (9) \text{\bf X}_i^{t+1}=\begin{dcases}\text{\bf X}_{best}^{t}+{\bf rand}\cdot({\bf X}_{best}^t-{\bf X}_i^t)+TF\cdot p^2\cdot({\bf X}_{best}^t-{\bf X}_i^t),\quad\text{if}\,\,\text{rand}<0.5\\[2ex]TF\cdot p^2\cdot{\bf X}_i^t,\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\text{if}\,\,\text{rand}\geq0.5\end{dcases}\tag{9} Xit+1=⎩⎨⎧Xbestt+rand⋅(Xbestt−Xit)+TF⋅p2⋅(Xbestt−Xit),ifrand<0.5TF⋅p2⋅Xit,ifrand≥0.5(9) p = ( 1 − t t max ) t / t max (10) p=\left(1-\frac{t}{t_{\max}}\right)^{t/t_{\max}}\tag{10} p=(1−tmaxt)t/tmax(10)其中, T F TF TF是一个值为1或−1的随机数。
2、TSO算法伪代码
金枪鱼通过两种觅食策略进行合作狩猎,然后找到猎物。对于TSO的优化过程,首先在搜索空间中随机生成种群。在每次迭代中,每个个体随机选择两种觅食策略中的一种执行,或根据概率 z z z选择重新生成搜索空间中的位置。在整个优化过程中,TSO的所有个体都会不断更新和计算,直到满足最终条件,然后返回最优个体和相应的适应度值。TSO伪代码如图1所示。

二、仿真实验与分析
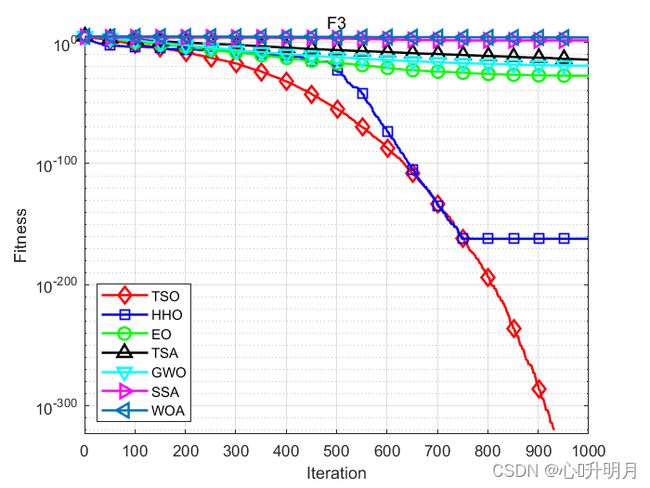
将TSO与HHO、EO、TSA、GWO、SSA和WOA进行对比,以文献[1]中的F1、F3(单峰函数/30维)、F10、F11(多峰函数/30维)、F20、F21(固定维度多峰函数/6维、4维)为例,种群规模设置为50,最大迭代次数设置为1000,每个算法独立运算30次。结果显示如下:


函数:F1
TSO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
HHO:最差值: 3.8853e-195, 最优值: 1.9148e-221, 平均值: 2.0518e-196, 标准差: 0, 秩和检验: 1.2118e-12
EO:最差值: 2.4784e-101, 最优值: 3.7885e-107, 平均值: 1.9732e-102, 标准差: 4.8432e-102, 秩和检验: 1.2118e-12
TSA:最差值: 7.8376e-51, 最优值: 4.3609e-55, 平均值: 3.2757e-52, 标准差: 1.4217e-51, 秩和检验: 1.2118e-12
GWO:最差值: 8.7456e-69, 最优值: 1.7964e-72, 平均值: 4.7536e-70, 标准差: 1.6422e-69, 秩和检验: 1.2118e-12
SSA:最差值: 1.3295e-08, 最优值: 5.7796e-09, 平均值: 9.0763e-09, 标准差: 2.0069e-09, 秩和检验: 1.2118e-12
WOA:最差值: 2.0236e-171, 最优值: 1.8763e-186, 平均值: 1.088e-172, 标准差: 0, 秩和检验: 1.2118e-12
函数:F3
TSO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
HHO:最差值: 2.676e-161, 最优值: 8.6031e-195, 平均值: 8.9199e-163, 标准差: 4.9702e-162, 秩和检验: 1.2118e-12
EO:最差值: 7.1477e-27, 最优值: 3.7095e-35, 平均值: 3.0203e-28, 标准差: 1.299e-27, 秩和检验: 1.2118e-12
TSA:最差值: 1.905e-13, 最优值: 1.3326e-28, 平均值: 6.4746e-15, 标准差: 3.4762e-14, 秩和检验: 1.2118e-12
GWO:最差值: 6.6695e-19, 最优值: 6.8916e-27, 平均值: 6.8592e-20, 标准差: 1.5409e-19, 秩和检验: 1.2118e-12
SSA:最差值: 140.278, 最优值: 5.2169, 平均值: 46.9785, 标准差: 34.4463, 秩和检验: 1.2118e-12
WOA:最差值: 24685.2948, 最优值: 1019.7777, 平均值: 11455.0503, 标准差: 5820.31, 秩和检验: 1.2118e-12
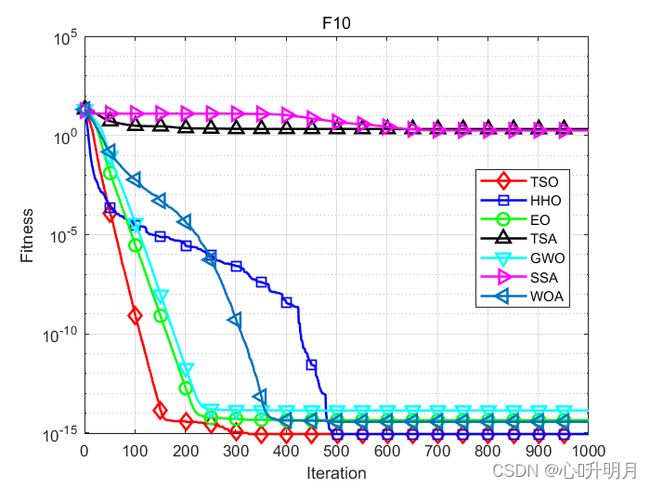
函数:F10
TSO:最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
HHO:最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
EO:最差值: 4.4409e-15, 最优值: 4.4409e-15, 平均值: 4.4409e-15, 标准差: 0, 秩和检验: 1.6853e-14
TSA:最差值: 3.5268, 最优值: 7.9936e-15, 平均值: 2.0839, 标准差: 1.5156, 秩和检验: 1.1824e-12
GWO:最差值: 1.5099e-14, 最优值: 7.9936e-15, 平均值: 1.3678e-14, 标准差: 2.5721e-15, 秩和检验: 2.5728e-13
SSA:最差值: 3.8858, 最优值: 1.9806e-05, 平均值: 1.789, 标准差: 1.0741, 秩和检验: 1.2118e-12
WOA:最差值: 7.9936e-15, 最优值: 8.8818e-16, 平均值: 3.7303e-15, 标准差: 2.1681e-15, 秩和检验: 2.642e-08
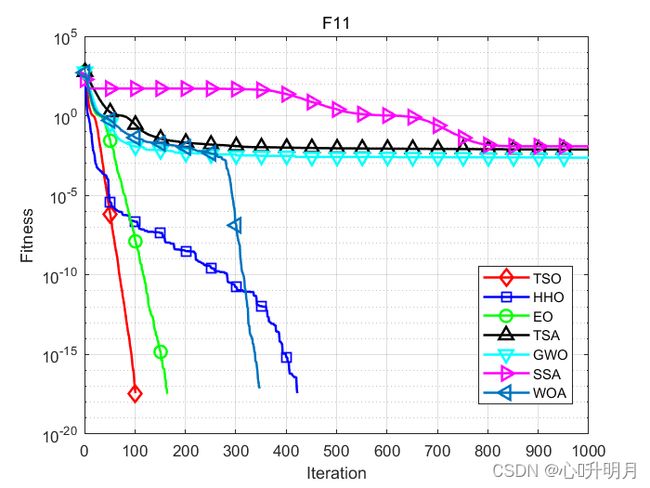
函数:F11
TSO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
HHO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
EO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
TSA:最差值: 0.051756, 最优值: 0, 平均值: 0.0075514, 标准差: 0.0099096, 秩和检验: 8.8658e-07
GWO:最差值: 0.027924, 最优值: 0, 平均值: 0.0023552, 标准差: 0.0074256, 秩和检验: 0.081523
SSA:最差值: 0.068771, 最优值: 2.5447e-08, 平均值: 0.012144, 标准差: 0.013381, 秩和检验: 1.2118e-12
WOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F20
TSO:最差值: -3.2031, 最优值: -3.322, 平均值: -3.2586, 标准差: 0.060328, 秩和检验: 1
HHO:最差值: -3.2025, 最优值: -3.322, 平均值: -3.2545, 标准差: 0.059959, 秩和检验: 0.00034656
EO:最差值: -3.1974, 最优值: -3.322, 平均值: -3.2544, 标准差: 0.060101, 秩和检验: 0.17391
TSA:最差值: -3.0832, 最优值: -3.3215, 平均值: -3.2513, 标准差: 0.070318, 秩和检验: 0.00083562
GWO:最差值: -3.1327, 最优值: -3.322, 平均值: -3.2468, 标准差: 0.069581, 秩和检验: 0.00034656
SSA:最差值: -3.1998, 最优值: -3.322, 平均值: -3.2103, 标准差: 0.030378, 秩和检验: 6.2047e-10
WOA:最差值: -3.0942, 最优值: -3.322, 平均值: -3.2418, 标准差: 0.080749, 秩和检验: 0.00083562
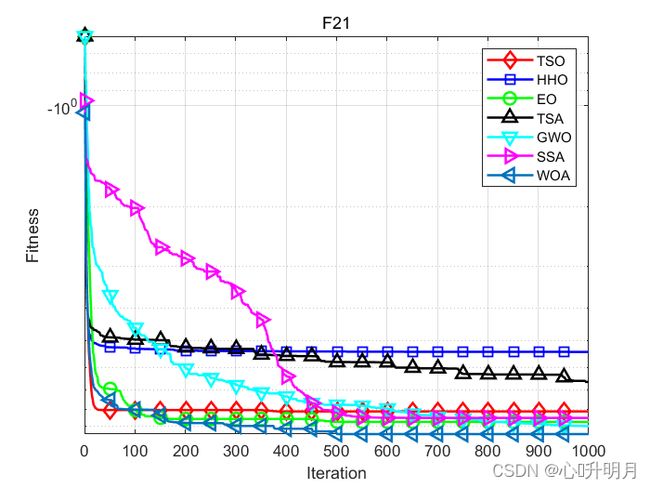
函数:F21
TSO:最差值: -5.0552, 最优值: -10.1532, 平均值: -8.114, 标准差: 2.5402, 秩和检验: 1
HHO:最差值: -5.0551, 最优值: -10.1528, 平均值: -5.395, 标准差: 1.2933, 秩和检验: 1.9883e-10
EO:最差值: -2.6305, 最优值: -10.1532, 平均值: -8.7129, 标准差: 2.4655, 秩和检验: 0.14135
TSA:最差值: -2.6166, 最优值: -10.1439, 平均值: -6.627, 标准差: 3.1565, 秩和检验: 1.1412e-05
GWO:最差值: -5.0552, 最优值: -10.1532, 平均值: -8.9695, 标准差: 2.1818, 秩和检验: 0.060583
SSA:最差值: -2.6305, 最优值: -10.1532, 平均值: -8.48, 标准差: 2.8942, 秩和检验: 0.039787
WOA:最差值: -5.0552, 最优值: -10.1532, 平均值: -9.4732, 标准差: 1.7625, 秩和检验: 0.039787
仿真结果表明:与其他比较算法相比,TSO算法具有更好的性能。
三、参考文献
[1] Lei Xie, Tong Han, Huan Zhou, et al. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization[J]. Computational Intelligence and Neuroscience, vol. 2021, Article ID 9210050, 22 pages, 2021.