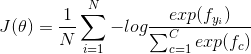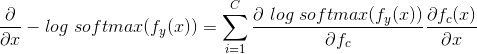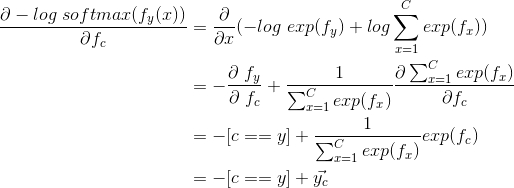cs224n学习笔记 4

1 一般的分类问题

1.1 softmax classifier

训练集的形式是，其中是inputs，是labels；在这里，我们做出一些约定，方便后面进行说明：我们认为是一个d维的向量，表示C个类别中的一类

当训练结束，进入预测阶段的时候，我们希望我们的模型能够预测"输入为x，类别为y”这件事的概率，我们可以借助训练得到的参数直接进行计算，计算的式子为，其中参数W是一个C*d的矩阵，该矩阵的第i行是预测输入类别为i时需要用到的参数，我们记W的第i行为

如此一来，上述公式的意义就比较明显了，可以看做是为输入x的类别是y这件事打了一个分数，而最后得到的概率就是对这个分数进行了一个softmax操作。为了后面方便表示，我们进一步约定：把“输入x的类别是y这件事打分”这个函数记为，即

预测的问题已经说明白了，那么就该考虑如何训练模型得到参数矩阵W。实际上方法也很简单，假设输入x的真实类别就是y，那么我们自然希望的概率尽量大，也就是希望的值尽量小，我们只要使用梯度下降的方法，将作为优化目标进行最小化，最终就可以得到W；当然，我们的训练集当中一共有N笔数据，所以object function的形式就是

在实现的过程中，还有一点需要注意：为了提升代码执行的效率以及方便书写，我们不会依次计算，我们会令，这样得到的f是一个C*1的列向量，它的每一个元素依次对应了

当矩阵W比较大，参数比较多的时候，还会涉及到一个老生常谈的话题，就是过拟合的问题。为了解决过拟合的问题，我们往往会在目标函数当中引入一个正则化的项，引入正则化因子之后softmax分类器的object function的形式为

1.2 交叉熵损失（Cross entropy）

在很多模型的训练过程中，我们都希望模型预测得到的向量和输入的标签的one-hot向量二者尽可能相似，但是这个“相似”要如何定义呢？比如对于某一条数据，模型预测得到的概率结果是向量[0.1 0.7 0.2]，而这条数据的标签是one-hot向量[0 1 0]，我要如何量化他们之间的相似性，来衡量我预测结果的优劣呢？

一个比较好的方法就是使用交叉熵：对于两个C维的向量、，是一个代表实际标签的one-hot向量，是我们预测得到的概率组成的结果向量，我们称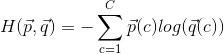的大小为二者的交叉熵；、之间的差异越大，他们的交叉熵也越大，反之则越小，因此我们可以把交叉熵作为我们要最小化的对象

对于1.1中的softmax classifier问题，针对其中的某一条数据，我们前面提到过要最小化的对象是。之前解释的出发点是要让正确预测的概率最大，现在我们可以从交叉熵的角度给出另外一种解释：这条数据的标签向量是一个只在第维是1的one-hot向量，模型预测得到的向量，、的交叉熵的值就是，所以最小化实际上就是最小化、之间的交叉熵

1.3 分类对象是词向量

当分类的对象是词向量的时候，我们在训练过程中，更新权重矩阵W的同时，一般还要更新参与训练的词的词向量，由此引发了两个可能产生问题的地方，需要特别注意：

第一，由于全部词向量的个数非常多，这样一来参数的个数就增加了很多，参数数量太多就更容易过拟合，因此需要一定的手段来进行遏制

第二，往往我们用来进行分类的单词的词向量，不是我们自己通过词嵌入算法得到的，而是直接下载别人通过大量的文本训练得到的现成的词向量，如果我们在自己训练的过程中，在已有的基础上对词向量进行了重新训练或者是更新，就可能造成下面的问题：别人在大量文本上训练，因此得到的TV、telly、television三个词的词向量比较接近，而我们自己的参与训练的文本因为比较小，只出现了TV和television这两个词，通过训练之后反而使得telly距离另外两个同义词的距离变得更大了。这显然是我们不希望看到的，对于这个问题的经验就是，如果自己参与训练的文本比较少，就不要轻易对词向量进行更新。

2 Window Classification

对于一般的机器学习问题，第1节的分类方法就是一个非常传统的解决方案，但是针对NLP领域，分类的对象如果是单词的话，第1节的方法往往是不能直接使用的，原因是对于语言来说，常常会出现一词多义的现象，在没有语境的前提下，对于一个单词进行分类会出现很多问题。比如seed这个单词，既可以做“播种种子”的意思，同时也可以做“铲除种子”的意思；再比如我想通过分类判断Paris这个词是否是一个地点，但是Paris作为巴黎来讲的时候就是一个地点，但是作为一个人名来讲的时候就不是一个地点

因此，在训练分类器的时候要把上下文考虑进去，这就是Window Classification的出发点

Window Classification其实也只是在一般的分类问题上进行了一点改变，假设原来原来词向量的长度是d，那么当我想要使用某个词进行训练的时候，我就以这个词为中心，以m为半径，将这2m+1个单词的词向量拼起来，作为一个(2m+1)*d维的向量进行训练，相应的，参数矩阵W的维度变成了。这样一来，Window Classification就化归成了一个一般的分类问题

在1中，给出了一般的分类问题的object function，但是没有计算更新时的梯度，这节给出分类问题的梯度计算

2.1 Window Classification梯度计算

一般分类问题的object function形式为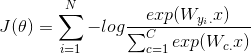，为了方便后面我们使用符号表示，我们再定义下面的几个符号：

，可以简记为

代表预测的结果向量

下面，我们将推导训练过程中每一次对词向量更新时使用的梯度

将求和号右边两部分分别计算

既然两部分都表示出来了，我们就可以求出原来要求的梯度的值，但是为了能够表示的比较精简，我们引入下面的几个符号：

,

是代表输入的实际类别的one-hot向量，根据上面的结果可知有

这么一来，就有，就得到了更新x时使用的梯度，更新W时使用的梯度课上没有给出具体求解过程，但是思路是一样的

2.2 实践中的注意点

在上面求x的梯度的过程中，我们一直试图引入更多的记号，把零散的数值整合成向量，把零散的向量整合成矩阵的形式，一方面是为了方便表示，另一方面是为了提升计算的效率

之所以矩阵运算比单独的元素或向量运算的速度要快，是因为底层有很多黑科技可以加速矩阵乘法的速度，如此一来能减少相当大的时间开销

3 神经网络

在1和2中，解决分类问题所使用的方法其实是logistic regression（虽然和很多地方讲解的logistic regression与上面使用的参数数量、激活函数的形式并不一样），这样产生的一个问题就是，在不进行维度映射的情况下，这样的方法只能作为一个线性分类器发挥作用，拟合能力及其有限；为了能够提升拟合能力，神经网络应运而生

神经网络往往是由很多层构成的，每层又有很多个神经元，从本质上来说，每个神经元都在执行一个logistic regression，前一层神经元的结果传到下一层的神经元上，使得模型能够拟合更为复杂的问题

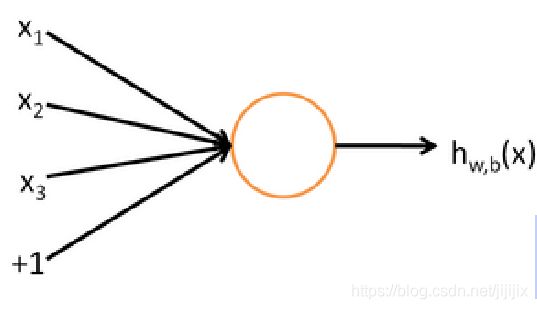
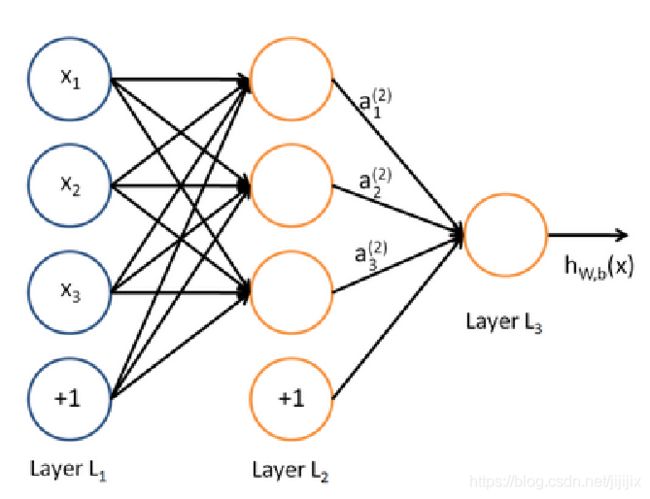
3.1 单个神经元结构

单个神经元的结构如图，首先确定一点，在表示神经网络的图中，一个神经元本身（图中橘色圆圈）代表的是一个数值大小，这个数值大小一般是一个向量某一维度上的值

右边从神经元中射出的箭头，代表的是这个神经元连向其他的神经元的“出口”，假设神经元本身的值大小是v，那么他作为“出口”连向其他神经元的时候也需要为连向的神经元提供一个值，但这个值的大小并不是v，而是h(v)，这里的h是一个激活函数，比如sigmoid函数

左边进入神经元的箭头，代表的是这个神经元的“入口”。这些箭头都是由其他神经元的“出口”连过来的，每一个“出口”提供一个数值，再乘上一个权重，累加起来就是神经元本身的数值v

如此一来，我们就可以说，神经元作为“入口”累加得到的值是，而神经元作为“出口”参与其他神经元运算时使用的值为，在本节中，我们默认激活函数是sigmoid函数，那么有

3.2 相邻两层神经网络之间的关系

如图是一个单层的神经网络结构（单层指只有一个隐藏层），第一层是输入层；第二层称为隐藏层，注意这里,,不是隐藏层神经元本身的值，而是经激活函数之后作为“出口”时的值；第三层是输出层，神经元的值经由激活函数之后，输出一个值，这就是这个模型的输出，我们记为

根据3.1中的分析，我们知道这个图中满足

如果我们以向量和矩阵的角度来认识相邻两层神经网络之间的关系，那么我们令，令所有权重组成一个矩阵，令所有偏置组成一个列向量，令所有输出值组成一个向量

根据上面的符号，有，这就是神经网络结构中相邻两层之间的关系。其中矩阵是一个维的矩阵，其中是前一层中神经元个数，是后一层中神经元的个数；向量则是维的列向量。

3.3 单层神经网络的结构

如图是一个单层的神经网络：

输入是一个20维的列向量，输入层和隐藏层之间的权重矩阵是一个维的矩阵（说明隐藏层神经元个数是8个），输入层和隐藏层之间的偏置向量是一个8维的列向量

隐藏层神经元的值组成一个8维的列向量，值为；经过激活函数后，得到一个8维的列向量，

在输出层中，输出一个数值s作为“得分”。隐藏层和输出层之间用一个维的参数矩阵来进行沟通，他们之间的关系是

但是s并不是我们直接的损失函数，在这个地方为了配合s这个“得分”，我们选择使用max-margin loss作为损失函数，这个损失函数的形式是。式子里符号的含义如下：“得分”是用label为1的“正样本”计算出的得分，“得分”是用label为0的“负样本”计算出的得分。注意虽然式子里带着一个max函数，但是我们的目标是要让的值最小，小意味着我们希望“正样本”得分尽量高，“负样本”得分尽量低。最后，max函数起到的作用是：当“正样本”得分比“负样本”得分大的值超过1的时候，我们就认为结果足够好了，直接取0，这样就不需要更多的训练，加快了模型收敛。

当然，这个例子只是神经网络的一个形式，事实上很多“组件”都可以进行替换：比如我们可以用Relu函数替代sigmoid作为激活函数；再比如输出层，我们可以对做softmax操作，得到一个的输出层，然后loss funciton改用交叉熵损失，这样一来就可以代替再对做max-margin loss

本节后面还对这个神经网络中每个变量进行了求导，但这个内容和下一节的内容有很大重复，所以放在下一节来写