人工智能实践-Tensorflow2.0 笔记1

1. 神经网络

1.1. 人工智能三学派

行为主义：构建感知-动作控制系统，如机器人
符号主义：实现理性思维，如专家系统
连接主义：仿脑神经连接，实现感性思维，如神经网络
当今人工智能主流方向–连接主义

1.2. 神经网络设计过程

1. 准备数据：采集大量“特征/标签”数据
2. 搭建网络：搭建神经网络结构
   全连接网络：网络前向传播求出预测值
   损失函数：定义预测值与真实值之间的差距；多种函数，例如MSE
3. 优化参数：训练网络获取最佳参数（反传），使损失函数最小，梯度下降法更新损失函数的参数
4. 应用网络：将网络保存为模型，输入新数据，输出分类或预测结果（前传）

1.3. 张量创建

Tensor: 张量，多维数组
阶： Tensor的维度
标量scalar -> 向量vector -> 矩阵matrix -> 张量tensor
数据类型：tf.int, tf.float …、tf.bool、tf.string
Tensor 创建：

1. tf.constant(张量内容，dtype=数据类型)
2. tf.convert_to_tensor(数据名，dtype=数据类型)，将 numpy 数据类型转换为 Tensor 数据类型
3. tf.zeros(维度)，维度：一维直接写个数，二维用[行，列]，多维用[n, m, j, k, …]
4. tf.ones(维度)
5. tf.fill(维度，指定值)，创建指定值的张量
6. tf.random.normal(维度，mean=均值，stddev=标准差)，生成正态分布的随机值
7. tf.random.truncated_normal(维度，mean=均值，stddev=标准差)，生成截断式正态分布的随机值
8. tf.random.uniform(维度，minval=最小值，maxval=最大值)

1.4. TF2 常用函数

1. tf.cast(张量名，dtype=数据类型)：强制tensor转换为该数据类型
2. tf.reduce_min(张量名)：计算tensor维度上元素的最小值
3. tf.reduce_max(张量名)：计算tensor维度上元素的最大值
   理解axis：在一个二维张量或数组中，可以通过调整axis等于0或1控制执行维度；axis=0代表跨行，axis=1代表跨列，如果不指定axis，则所有元素参与计算
4. tf.reduce_mean(张量名，axis=操作轴): 求平均值
5. tf.reduce_sum(张量名，axis=操作轴)：求和
6. tf.Variable(初始值)：将变量标记为“可训练”，被标记的变量会在反向传播中记录梯度信息
7. TF中的数学运算：四则运算–tf.add(张量1，张量2), tf.subtract, tf.multiply, tf.divide，平方次方开方–tf.square, tf.pow, tf.sqrt，矩阵乘–tf.matmul

1.5. TF2常用函数2

8. tf.data.Dataset.from_tensor_slices((输入特征，标签)): 从tensor切出数据集
9. tf.GradientTape: 求张量的梯度，一般使用 with 结构
10. enumerate: 枚举列表，元组或字符串
11. tf.one_hot(待转换数据，depth=几分类): 独热编码（one-hot encoding），在分类问题中，常用独热码表示标签，标记类别：1表示是，0表示非
12. tf.nn.softmax: n分类的n个输出，通过softmax()函数后将符合概率分布；数字只有符合概率分布后，才可以与独热码的标签作比较
13. w.assign_sub: 常用于参数的自更新
14. tf.argmax(张量名，axis=操作轴)：返回张量沿指定维度最大值的索引

1.6. 鸢尾花数据集读入

鸢尾花数据集来自于sklearn包的datasets

1.7. 神经网络实现鸢尾花分类

步骤：

1. 准备数据：数据集读入、数据集乱序、生成训练集和测试集(即 x_train/y_train, x_test/y_test)、配成(特征，标签)对，每次读入一小撮(batch)
2. 搭建网络：定义神经网络中所有可训练参数
3. 参数优化：嵌套循环迭代，with结构更新参数，显示当前loss
4. 测试效果：计算当前参数前向传播后的准确率，显示当前acc
5. acc/loss 可视化
   参考例子

1.8. Tensorflow2 安装

pip install tensorflow

2. 神经网络优化

神经网络复杂度、指数衰减学习率、激活函数、损失函数、欠拟合与过拟合、正则化减少过拟合、优化器更新网络参数

2.1. 预备知识

1. tf.greater(张量1，张量2)：比较大小（按元素）
2. tf.where(条件语句，真返回A，假返回B)
3. np.random.RandomState.rand(维度)：返回0-1之间的随机数
4. np.vstack((a, b)): 将两个数组按垂直方向叠加
5. np.mgrid[], x.ravel(), np.c_[] : 生成网格坐标点，将x变为一维数组，数组配对后输出
   

2.2. 复杂度、学习率

nn复杂度：多采用nn层数和nn参数的个数表示
空间复杂度：

• 层数=隐藏层的层数+1个输出层
• 总参数=总w+总b

时间复杂度：

• 乘法运算次数

学习率：参数每次更新的幅度
$$w_{t+1}=w_t-lr\ast \frac{\partial loss}{\partial w_t}$$
学习率设置策略：可以先用较大的学习率，快速得到较优解，然后逐步减小学习率，使模型在训练后期稳定，动态改变学习率
指数衰减学习率=初始学习率*学习率衰减率^(当前轮数/多少轮衰减一次)
lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)

2.3. 激活函数

线性模型表达力不够，所以要用非线性模型。
优秀的激活函数：非线性、可微性、单调性、近似恒等性
激活函数输出值的范围：

• 激活函数输出为有限值时，基于梯度的优化方法更稳定
• 激活函数输出为无限值时，建议调小学习率

常用激活函数：

1. sigmoid 函数
   $$f(x)=\frac{1}{1+e^{-x}}tf.nn.sigmoid(x)$$
   

2. Tanh 函数
   $$f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}tf.nn.tanh(x)$$
   

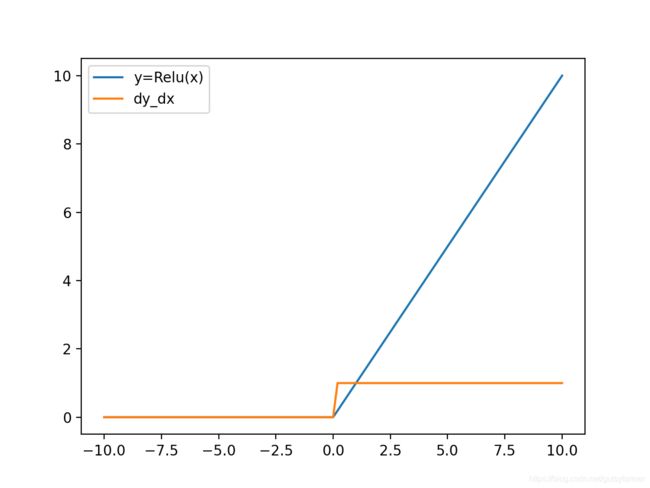
3. Relu 函数
   $$f(x)=max(x,0)tf.nn.relu(x)$$
   

4. Leaky Relu 函数
   $$f(x)=max(ax,x)tf.nn.leaky\_relu(x)$$

对初学者的建议：首选relu激活函数，学习率设置较小值，输入特征标准化(0为均值，1为标准差)，初始参数中心化

2.4. 损失函数

损失函数(loss)：预测值(y)与已知答案(y_)的差距
nn优化目标：loss最小；mse(Mean Squared Error)，自定义，ce(Cross Entropy)
均方误差mse:
$$\begin{gathered} \text{MSE}(y\_,y)=\frac{{\sum }_{i=1}^n(y-y\_{)}^2}{n} \\ loss\_mse=tf.reduce\_mean(tf.square(y\_-y)) \end{gathered}$$
交叉熵损失函数CE(Cross Entropy)：表征两个概率分布之间的距离
$$\begin{gathered} H(y\_,y)=-\sum y\_\ast \ln y \\ tf.losses.categorical\_crossentropy(y\_,y) \end{gathered}$$

softmax 与交叉熵结合：输出先过softmax函数，再计算y与y_的交叉熵损失函数
tf.nn.softmax_cross_entropy_with_logits(y_, y)
或者
y_pro = tf.nn.softmax(y)
loss_ce = tf.losses.categorical_crossentropy(y_, y_pro)

2.5. 过拟合

欠拟合：对数据集学习的不够彻底
正拟合：对测试数据、新数据拟合的都很好
过拟合：对当前数据拟合很好，但对新数据却无法拟合，模型缺乏泛化力
正则化缓解过拟合：正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了训练数据的噪声（一般不正则化b）
$$\begin{gathered} loss=loss\_mse+REGULARIZER\ast loss(w) \\ REGULARIZER=0.03 \\ los{s}_{l1}(w)=\sum _i|w_i| \\ los{s}_{l2}(w)=\sum _i|w_i^2| \\ tf.nn.l2\_loss(w)=sum(w\ast \ast 2)/2 \end{gathered}$$

2.6. 优化器

优化器是引导神经网络更新参数的工具
假设：待优化参数w，损失函数loss，学习率lr，每次迭代一个batch，t表示当前batch迭代的总次数

1. 计算t时刻损失函数关于当前参数的梯度$g_t=\nabla loss=\frac{\partial loss}{\partial (w_t)}$
2. 计算t时刻一阶动量$m_t$和二阶动量$V_t$
3. 计算t时刻下降梯度：${\eta }_t=lr\cdot \frac{m_t}{{\sqrt{V}}_t}$
4. 计算t+1时刻参数：$W_{t+1}=W_t-{\eta }_t=W_t-lr\cdot \frac{m_t}{{\sqrt{V}}_t}$

注：一阶动量是与梯度相关的函数，二阶动量是与梯度平方相关的函数，不同的优化器，实质上只是定义了不同的一阶动量和二阶动量公式

五种优化器：

1. SGD （无momentum）
   $m_t=g_t{V}_t=1$
   $W_{t+1}=W_t-{\eta }_t=W_t-lr\cdot \frac{m_t}{{\sqrt{V}}_t}=W_t-lr\cdot g_t$
2. SGDM （含 momentum），在SGD基础上增加一阶动量
   $m_t=\beta \cdot m_{t-1}+(1-\beta )\cdot g_t{V}_t=1$
   $\beta =0.99m_{t0}=0$
3. Adagrad, 在SGD基础上增加二阶动量
   $m_t=g_t{V}_t={\sum }_{\tau =1}^t{g}_{\tau }^2$
4. RMSProp, SGD基础上增加二阶动量
   $m_t=g_t{V}_t=\beta \cdot V_{t-1}+(1-\beta )\cdot g_t^2$
5. Adam, 同时结合SGDM一阶动量和RMSProp二阶动量，创建修正项，使用修正量更新参数
   $m_t={\beta }_1\cdot m_{t-1}+(1-{\beta }_1)\cdot g_t$
   修正一阶动量的偏差：$\widehat{m_t}=\frac{m_t}{1-{\beta }_1^t}$
   $V_t={\beta }_2\cdot V_{t-1}+(1-{\beta }_2)\cdot g_t^2$
   修正二阶动量的偏差：$\widehat{V_t}=\frac{V_t}{1-{\beta }_2^t}$
   ${\eta }_t=lr\cdot \frac{{\hat{m}}_t}{\sqrt{{\hat{V}}_t}}$
   $W_{t+1}=W_t-{\eta }_t=W_t-lr\cdot \frac{\frac{m_t}{1-{\beta }_1^t}}{\sqrt{\frac{V_t}{1-{\beta }_2^t}}}$

3. 使用keras快速搭建神经网络

搭建网络八股、iris代码复现、mnist数据集、训练mnist数据集、Fashion数据集

3.1. 六步法

import: 导入相关模块
train, test: 告知要喂入网络的训练集和测试集
model = tf.keras.models.Sequential: 搭建网络结构，逐层描述网络，相当于前向传播
model.compile: 配置训练方法–优化器、损失函数、评测指标
model.fit: 执行训练过程
model.summary: 打印网络结构和参数统计

1. model = tf.keras.models.Sequential([ 网络结构 ])
   网络结构：

   拉直层：tf.keras.layers.Flatten()

   全连接层：tf.keras.layers.Dense(神经元个数, activation=“激活函数”, kernel_regularizer=哪种正则化)，activation（字符串给出）可选–relu, softmax, sigmoid, tanh，kernel_regularizer 可选–tf.keras.regularizers.l1(), tf.keras.regularizers.l2()

   卷积层：tf.keras.layers.Conv2D(filters=卷积核个数，kernel_size=卷积核尺寸，strides=卷积步长，padding=“valid"or"same”)

   LSTM层：tf.keras.layers.LSTM()

2. model.compile(optimizer=优化器, loss=损失函数, metrics=[‘准确率’])
   optimizer可选：sgd–tf.keras.optimizers.SGD, adagrad, adadelta, adam
   loss可选：mse–tf.keras.losses.MeanSquaredError(), sparse_categorical_crossentropy
   metrics可选：accuracy, categorical_accuracy, sparse_categorical_accuracy

3. model.fit(训练集的输入特征，训练集的标签，batch_size=, epochs=, validation_data=(测试集的输入特征，测试集的标签)，validation_split=从训练集划分多少比例给测试集，validation_freq=多少次epoch测试一次)

3.2. 自定义model

class IrisModel(Model):
	def __init__(self):
		super(IrisModel, self).__init__()
		# 定义网络结构块
		self.d1 = Dense(3)

	del call(self, x):
		# 调用网络结构块，实现前向传播
		y = self.d1(x)
		return y

model = IrisModel()

3.3. mnist数据集

mnist数据集包含了7万张手写数字图片

3.4. FASHION数据集

fashion数据集包含了7万张衣裤等图片和标签