深度学习——从感知机到BP神经网络
深度学习入门(一)——从感知机到BP神经网络
- 前言
- 一、感知机
-
- 1、从逻辑电路开始
- 2、单层感知机
- 3、多层感知机
- 二、神经网络
-
- 1、从感知机到神经网络
- 2、激活函数
- 3、几种激活函数
-
- 3.1 sigmoid函数
- 3.2 tanh激活函数
- 3.3 ReLU函数
- 4、小结
- 三、误差反向传播算法及BP神经网络
-
- 1、误差反向传播算法
- 2、梯度下降法
-
- 2.1 梯度下降法的数学推导
- 2.2 多层感知机的数学推导
- 3、BP神经网络具体实现
-
- 3.1 BP神经网络的实现步骤如下:
- 3.2 BP神经网络结构
- 3.2.1 Affine层
- 3.2.2 ReLU层
- 3.2.3 softmax层
- 四、结论
前言
最近基于研究方向及硕士课程的契机,开始学习深度学习有关知识。通过这篇博客对自己的学习进度做一个展示,也希望能够帮助到初学深度学习的各位。
一、感知机
感知机是神经网络的学习的基础,只有理解了感知机的原理和构成,才能对神经网络有一个具体的概念。
1、从逻辑电路开始
| 输入 x 1 x_1 x1 | 输入 x 2 x_2 x2 | 输出y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
我们可以认为,与门电路仅在输入A与输入B同时为1时,输出为1.如果用数学表达式表示,可以写为以下形式:

我们设 ( w 1 , w 2 , θ ) (w_1,w_2,\theta) (w1,w2,θ)分别为(1,1,1),那么只有当 x 1 , x 2 x_1,x_2 x1,x2同时为1时,y输出为1,可以正确表述与门逻辑。
同样,我们可以用下面这个图来表示门逻辑电路,将前面的表达式在此图上表示的话,我们可以看到,与门逻辑依然是成立的。
如果将上图视为一个神经网络,那么就是一个感知机了。
2、单层感知机
感知机(perceptron)由神经元组成,单层结构如上图所示,输入层接收外界输入信号后传递给输出层。
在感知机中, w 1 , w 2 , θ w_1,w_2,\theta w1,w2,θ分别称为权重和偏置, x 1 , x 2 x_1,x_2 x1,x2为输入信号,y为输出信号。当 w 1 ∗ x 1 + w 2 ∗ x 2 > θ w_1*x_1+w_2*x_2>\theta w1∗x1+w2∗x2>θ时,y有输出1,否则输出为0.
感知机的概念就是如此简单,使用一个单层感知机,可以成功实现与门、与非门、或门三种逻辑电路。
3、多层感知机
单层感知机只有输出神经元进行激活函数处理,即只有一层功能神经元(function neuron),只能解决线性可分(linearly separable)问题,而不能解决非线性可分问题,如异或门。但感知机的优势在于,它可以进行多层感知机的叠加,从而解决非线性问题。
| 输入 x 1 x_1 x1 | 输入 x 2 x_2 x2 | 输出y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
可以看到,这个逻辑无法用线性方程进行表示。
但是在数字电路中,我们知道,一个异或门可以与门、与非门和或门组合实现一个异或门,结构如下:

如果用单层感知机表示与非门、或门和与门,那么我们同样可以用单层感知机进行组合来实现异或门。

实际上,一个复杂的多层感知机已经能够表示一个计算机的工作!这是因为,计算机实际上仍是由数量巨大的基本逻辑门电路组成的。
二、神经网络
神经网络与感知机有很多共同点,在学习了感知机后,我们就可以开始神经网络的学习了。
1、从感知机到神经网络
用图来表示神经网络的话,如下图所示:

最左边一列称为输入层,最右边一列称为输出层,中间一列称为隐藏层。设计一个神经网络的时候,输入层、输出层往往是固定的,而隐藏层可以任意指定(在后面的例子中我们可以深入理解这一句话)。神经网络同样是由输入信号输入至输入层,经过隐藏层的传播后,在输出层进行输出。
可以用一个不恰当的例子进行说明:。
我们把圆圈想象成一个个池塘,而圆圈之间的连接线想象为池塘之间的沟渠。我们把水注入称为输入层的池塘中,让水流通过沟渠流到其他池塘之中。由于沟渠深度长度不同,有的池塘之间难以流过水流,有的池塘之间却很容易联通。最后,我们在称为输出层的池塘中,统计每个输出层池塘中的水的体积,这个体积就是我们想要的数据
我们可以看到,神经网络的形状类似于上一章感知机的形状。但是我们要知道,感知机中,我们更加关注圆圈(即神经元),而在神经网络中,关键不是圆圈(神经元)而是圆圈之间的连接线(神经元之间的连接)。每一个连接线对应一个不同的权值(即权重),对神经网络的训练即对这些权值进行更新。
OK,我们现在对神经网络有了一个大概的了解。
接下来让我们了解一下激活函数的概念。
2、激活函数
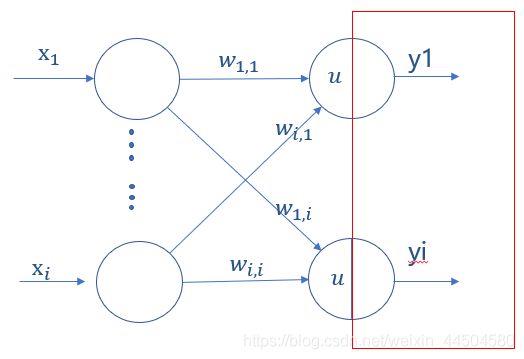
在神经元之中可以分为两部分,其结构如下图所示:

神经元的前半部分用来计算总和输入值,其输入值为 x = a ∗ w a + b ∗ w b + c ∗ w c x=a*w_a+b*w_b+c*w_c x=a∗wa+b∗wb+c∗wc,在感知机中 y = x y=x y=x,而在神经网络中 y = f ( x ) y=f(x) y=f(x),这个 f f f就是激活函数。
激活函数用来加入非线性因素,解决线性模型不能解决的问题.
由感知机可知,利用单层的感知机,输出的是一个线性函数。如果不使用激活函数,我们的每一层输出只是承接了上一层输入函数的线性变换,无论神经网络有多少层,输出都是输入的线性组合。激活函数给神经元引入非线性因素,使得神经网络可以逼近任何非线性函数,这样神经网络就可以应用到非线性模型中。
从数学角度来看:
激活函数可以用来组合训练数据的特征。

图中表达式为: x 3 = w 1 ∗ x 1 + w 2 ∗ x 2 x_3=w_1*x_1+w_2*x_2 x3=w1∗x1+w2∗x2
激活函数使用sigmoid函数:
根据泰勒展开:
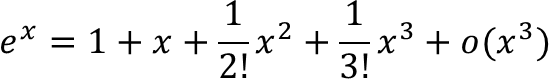
这样,就能把输入数据进行两两组合或者其他组合。
3、几种激活函数
常用的激活函数有3种,分别是sigmoid函数、tanh函数、ReLU函数,接下来我们一一介绍并分析其优缺点。
3.1 sigmoid函数
其函数式为:

其导数为:

sigmoid函数是最常用的激活函数,该函数在[-2.5,2.5]范围内迅速上升,并趋近于1,有着良好的导通性。但是其有几个缺点:
- 饱和时梯度值非常小。因此在使用梯度下降法时,得到的梯度就会非常小,在BP神经网络中权重得不到有效的更新,即梯度消失。
- 如果该层的权重初始化使得 f ( x ) f(x) f(x)处于饱和状态时,网络的权重基本无法更新。
- sigmoid的output不是0均值(即zero-centered),这是不可取的。因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。产生的结果就是对w求局部梯度都为正,这样在反向传播过程中w要么都往正方向更新,要么都往负方向更新,导致收敛缓慢。
由于BP神经网络的核心即反向传播算法,因此在BP神经网络中应尽可能避免使用sigmoid函数作为激活函数。
3.2 tanh激活函数
其函数表达式为: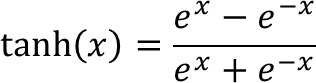

其导数为:
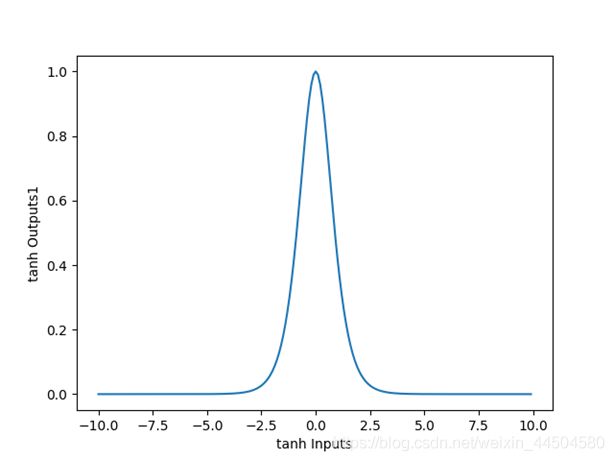
与sigmoid函数比较,tanh函数有以下优势:
- tanh的输出范围为(-1,1),解决了sigmoid函数不是0均值输出问题。
- tanh的导数范围在(0,1)之间,相比sigmoid的(0.0.25),梯度消失的问题得到缓解,但仍然存在。
3.3 ReLU函数
其函数表达式为:

其导数为:

相比sigmoid与tanh:
- ReLU解决了梯度消失问题,收敛速度更快,但要防范ReLU的梯度爆炸。
- ReLU在负半区的导数为0,表示梯度为0,这个神经元就不会被训练,即稀疏性。
- 因为ReLU函数在正半区的导数为常值,当神经网络很深时,梯度增长会比较大,会得到一个非常大的权重数值更新。
4、小结
将激活函数引入后,我们已经得到了一个完整的神经网络结构。

输入信号输入至神经元,与权重相乘后相加,再经过激活函数激活后,便得到输出数据,将输出数据传递给下一层,这就是神经网络的正向处理流。
我们终于成功追踪到了神经网络的信号——从信号进入神经网络,通过神经网络各层,并得到最终输出层的输出信号。
接下来该做些什么呢?
让我们先复习一下前面提及的最关键的一句话:在神经网络中,关键不是圆圈(神经元)而是圆圈之间的连接线(神经元之间的连接)。
带着这一句话,我们可以走进误差反向传播算法,并学习第一个神经网络——BP神经网络。
三、误差反向传播算法及BP神经网络
1、误差反向传播算法
我们接下来该做的事情是:将神经网络的输出值与训练样本中的输出值进行比较,计算出误差。我们需要用这个误差来调整神经网络本身,进而改进神经网络输出值——这就是误差反向传播算法实现的功能。即下图所示:

在多输入节点的情况下,我们应该如何将输出误差值分配到每一个输入节点呢?
——我们使用“不等分误差”来实现:按照输入节点不同的权重,将输入误差进行不等分,随后反向传播。
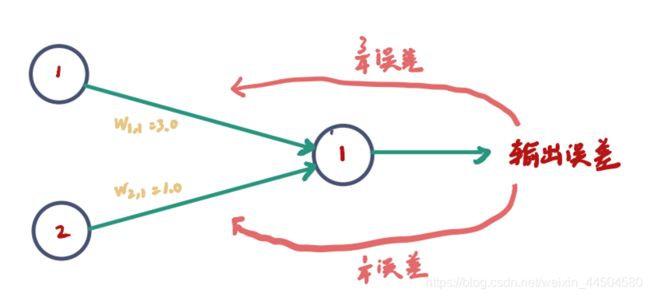
综合前面学习的知识,我们可以发现,权重在两件事情上发挥了作用:
- 在神经网络中,我们使用权重将信号从输入向前传播到输出层。
- 使用权重,将误差从输出反向传播到网络中。
误差反向传播算法基本思想:
| 学习过程由信号的正向传播与误差的反向传播两个过程组成:
| (1)正向传播:输入样本——>输入层——>隐藏层——>输出层
| (2)误差反向传播:输出误差——>隐藏层——>输入层
| 其目的主要是通过将输出误差反向传播,将误差分摊给各层所有单元,从而获得各层单元的误差信号,进而修正各单元的权重(其过程是一个权重调整的过程)。
接下来我们来看当有多个输出节点时,误差反向传播的具体过程:
反向第一层:
设由训练数据提供的所期望的输出值为 t 1 t_1 t1,实际输出值为 o 1 o_1 o1,则第一个输出节点的误差: e 1 = t 1 − o 1 e_1=t_1-o_1 e1=t1−o1,同样,对于第二个节点,我们使用相同方法计算。

继续反向传递:
由反向第一层向第二层传递,我们设 e 2 e_2 e2 , _, , 1 _1 1=链接 w 1 w_1 w1 , _, , 1 _1 1和链接 w 1 w_1 w1 , _, , 2 _2 2上分割误差之和:


到目前为止,我们已经可以将误差反向传播到网络的每一层,那么如何让误差来指导调整链接权重呢?
我们再来回想一下误差的定义:
——设由训练数据提供的所期望的输出值为 t 1 t_1 t1,实际输出值为 o 1 o_1 o1,则第一个输出节点的误差: e 1 = t 1 − o 1 e_1=t_1-o_1 e1=t1−o1
那么要使神经网络更加优良,就要使误差尽可能小。
从而,误差来指导如何调整链接权重问题变成了求误差函数最小值问题。
我们以网络误差的评分为目标函数,使用梯度下降法来求解误差函数最小值。
2、梯度下降法
我们可以想象为一个小球沿着山坡下降的方向滚落,直至滚落至山谷之中。

2.1 梯度下降法的数学推导
2.2 多层感知机的数学推导
3、BP神经网络具体实现
3.1 BP神经网络的实现步骤如下:
3.2 BP神经网络结构
3.2.1 Affine层
// affine
import numpy
class Affine:
def __init__(self,W,b):
self.W=W
self.b=b
self.x=None
self.dW=None
self.db=None
// 初始化
def forword(self,x):
self.x=x
out=numpy.dot(x,self.W)+self.b;
//前向传递
def backward(self,dout):
dx=numpy.dot(dout,self.W.T)
self.dW=numoy.dot(self.x.T,dout)
self.db=numpy.sum(dout,axis=0)
// 向后传播
return dx
3.2.2 ReLU层
即激活函数层,在BP神经网络中使用ReLU作为激活函数。
选择ReLU层作为激活函数的原因:
在前面我们讲过,由于ReLU在负半区的导数为0,表示梯度为0,这个神经元就不会被训练,即稀疏性:
如果正向传播时输入x>0,则反向传播会将上游的值原封不动传给下游。
如果正向传播时x小于0,则反向传播中传给下游的信号会停止在此处。
// ReLU
import numpy
class ReLU:
def __init__(self):
self.mask=None
// 初始化
def forword(self,x):
self.mask=(x<=0)
out[self.mask]=0
//前向传递
def backward(self,dout):
dout[self.mask]=0
dx=dout
// 向后传播
return dx
3.2.3 softmax层
即输出层——将输出值正规化后再输出。
四、结论
这篇文章简要写了我在学习神经网络的学习历程——从感知机开始到BP神经网络。
目前就先写到这里,
在下一篇我会继续更新关于CNN的介绍。