时间复杂度和空间复杂度
目录
1.时间复杂度
1.时间复杂度的概念和计算方法
2.几个简单算法的时间复杂度
1.循环嵌套
2.二分查找
3.冒泡排序
2.空间复杂度
1.空间复杂度的概念和计算方法
2.几个简单算法的时间复杂度
1.未定数组
2.递归函数
1.时间复杂度
1.时间复杂度的概念和计算方法
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
由于不同计算机运行程序效率不同,我们不能用时间长短表示时间复杂度,但是我们可以从计算程序运行次数来计算其时间复杂度。注意!时间复杂度不计算时间,计算次数。
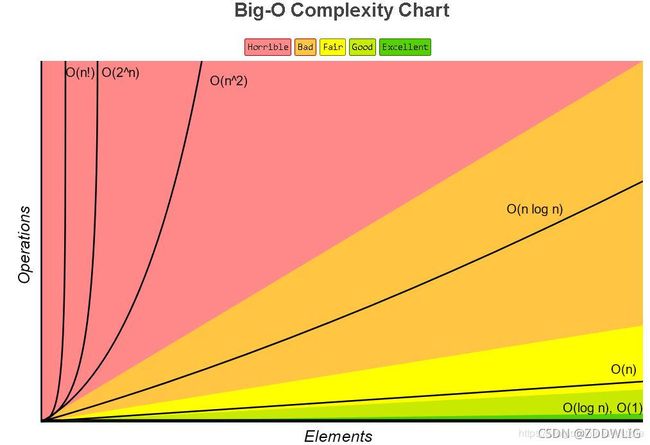
我们利用函数的变化率比较出常见时间复杂度的大小如下(考虑输入方便性,这里log默认以2为底)
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
时间复杂度越小,程序运行越快。我们来直观地比较一下几种时间复杂度程序的效率
2.几个简单算法的时间复杂度
1.循环嵌套
若有k个循环嵌套在一起且每个循环均进行N的线性函数次循环,则其时间复杂度为O(N^k),例如下面这个程序的时间复杂度为O(N^2),但是要注意的是,不是有几层循环时间复杂度就是N的几次幂,每个循环一定要进行N的线性函数次!
int main()
{
int i, j, N = 10, k = 10;
for (i = 0;i2.二分查找
计算二分查找的时间复杂度我们可以考虑最佳时间复杂度,平均时间复杂度,最糟时间复杂度,但是我们通常考虑最糟时间复杂度,不清楚二分查找思想的请看:C语言实现二分查找。我们设最糟的情况程序要进行x次,二分x次后元素个数从N变为1,每次二分元素个数都变为原来的1/2,显然这是一个首项为N,公比为1/2的等比数列,已得N*(1/2)^x=1;解的x为logN
int binary_search(int arr[],int k,int sz)
{
int left = 0;
int right = sz - 1;
while (left<=right)
{
int mid = (left + right) / 2;
if (arr[mid] < k)
{
left = mid + 1;
}
else if (arr[mid]>k)
{
right = mid - 1;
}
else
{
return mid;
}
}
return -1;
}3.冒泡排序
冒泡排序我们还是考虑最糟的情况,不清楚冒泡排序思想的请看:C语言实现冒泡排序。我们第一次外循环进行N次内循环,第二次进行N-1次内循环......最后进行1次内循环,利用等差数列求和,我们易得程序总共进行次数为N*(N+1)/2次,取N最高次幂N^2得时间复杂度为O(N^2)
void bubble_sort(int arr[],int sz)
{
int i, j,flag=1;
for (i=0;i arr[j + 1])
{
int tpm = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tpm;
flag=0;
}
}
if(flag==1)
{
break;
}
}
} 2.空间复杂度
1.空间复杂度的概念和计算方法
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了,因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。
与时间复杂度类似地,我们计算空间复杂度不能直接计算一个程序所占空间,而是计算变量的个数
常数个变量其空间复杂度为O(1),N个变量其空间复杂度为O(N),其他类推......
2.几个简单算法的时间复杂度
1.未定数组
一个长度为N的数组其空间复杂度为O(N),非常好理解,N个元素相当于创建了N个变量
int[] m = new int[n]
for(i=1; i<=n; ++i)
{
j = i;
j++;
}2.递归函数
计算机每调用一次函数就需要在内存中先开辟一块空间再执行函数内部的内容,所以递归函数有一个弊病:当递归次数过大时可能发生Stackoverflow,即栈溢出,程序无法运行。
int fac(int x)
{
if (x > 1)
return x*fac(x - 1);
else if (x = 1)
return 1;
}