A Few Useful Things to Know About Machine Learning 中英文对比和笔记

原文/翻译

似乎是CS231n推荐的文章，之前读了个开头扔掉了，最近被老板逼着做classification，所以拿出来精读。CSDN和全网没有全文翻译，有不少每个section翻译两句话的，也有不少翻译了一半的。直到我自己翻译才发现太TM的长了。大部分是机翻，然后根据自己的理解调整了一些，为了排版舒服，我自己的bb就加成了引用。我也不知道合不合规，反正我有备份。

原文引用：
Pedro Domingos. 2012. A few useful things to know about machine learning. Commun. ACM 55, 10 (October 2012), 78–87. DOI:https://doi.org/10.1145/2347736.2347755

原文地址

0. Introduction / 简介

Machine learning systems automatically learn programs from data. This is often a very attractive alternative to manually constructing them, and in the last decade the use of machine learning has spread rapidly throughout computer science and beyond. Machine learning is used in Web search, spam filters, recommender systems, ad placement, credit scoring, fraud detection, stock trading, drug design, and many other applications. A recent report from the McKinsey Global Institute asserts that machine learning (a.k.a. data mining or predictive analytics) will be the driver of the next big wave of innovation¹. Several fine textbooks are available to interested practitioners and researchers (for example, Mitchell² and Witten et al.³). However, much of the “folk knowledge” that is needed to successfully develop machine learning applications is not readily available in them. As a result, many machine learning projects take much longer than necessary or wind up producing less-than-ideal results. Yet much of this folk knowledge is fairly easy to communicate. This is the purpose of this article.

机器学习系统会自动从数据中学习程序。相较于手动构建程序，这通常是一种非常有吸引力的替代方法，并且在过去的十年中，机器学习的使用已迅速遍及整个计算机科学及其他领域。机器学习可用于Web搜索，垃圾邮件过滤器，推荐系统，广告放置，信用评分，欺诈检测，股票交易，药品设计以及许多其他应用程序中。麦肯锡全球研究所最近的一份报告断言，机器学习（又名数据挖掘或预测分析）将是下一波创新浪潮的驱动力。有兴趣的从业者和研究人员可以使用几本不错的的教科书（例如Mitchell和Witten等）。但是，成功开发机器学习应用程序所需的许多 “通俗知识” 并不容易在其中获得。结果，许多机器学习项目花费的时间比必要的要长得多，或者最终产生不理想的结果。但是，许多通俗知识相当容易交流。这就是本文的目的。

Many different types of machine learning exist, but for illustration purposes I will focus on the most mature and widely used one: classification. Nevertheless, the issues I will discuss apply across all of machine learning. A classifier is a system that inputs (typically) a vector of discrete and/or continuous feature values and outputs a single discrete value, the class. For example, a spam filter classifies email messages into “spam” or “not spam,” and its input may be a Boolean vector x = (x₁，…，x_j，…，x_d), where x_j = 1 if the jth word in the dictionary appears in the email and x_j = 0 otherwise. A learner inputs a training set of examples (x_i, y_i), where xi = (x₁，…，x_j，…，x_d) is an observed input and yi is the corresponding output, and outputs a classifier. The test of the learner is whether this classifier produces the correct output yt for future examples x_t (for example, whether the spam filter correctly classifies previously unseen email messages as spam or not spam).

存在许多不同类型的机器学习，但是出于说明目的，我将重点介绍最成熟且使用最广泛的一种：分类。不过，我将讨论的问题适用于所有机器学习。分类器是一个系统，输入一个通常由离散或连续特征值组成的向量，并输出单个离散值（类别）的系统。例如，垃圾邮件过滤器将电子邮件分类为“垃圾邮件”或“非垃圾邮件”，其输入可以是布尔向量x =（x₁，…，x_j，…，x_d），如果字典中的第j个单词出现在电子邮件中则x_j = 1，否则x_j = 0。Learner输入一组训练示例（x_i，y_i），其中x_i=（x₁，…，x_j，…，x_d）是观察到的输入，y_i是相应的输出，并输出分类器。Learner的考验是此分类器是否为将来的示例x_t生成正确的输出y_t（例如，垃圾邮件过滤器是否将以前未看到的电子邮件正确分类为垃圾邮件）。

1. Learning = Representation + Evaluation + Optimization / 学习=表示+评价+优化

Suppose you have an application that you think machine learning might be good for. The first problem facing you is the bewildering variety of learning algorithms available. Which one to use? There are literally thousands available, and hundreds more are published each year. The key to not getting lost in this huge space is to realize that it consists of combinations of just three components. The components are:

假设您有一个您认为机器学习可能会有用的应用程序。您面临的第一个问题在多得可怕的可用的学习算法中选择一个。确实有数千种可用，而且每年还会发布超过百种。在如此巨大的空间中不迷失的关键是要意识到它仅由三个组件组成。这些组件是：

• Representation. A classifier must be represented in some formal language that the computer can handle. Conversely, choosing a representation for a learner is tantamount to choosing the set of classifiers that it can possibly learn. This set is called the hypothesis space of the learner. If a classifier is not in the hypothesis space, it cannot be learned. A related question, that I address later, is how to represent the input, in other words, what features to use.
• 表示。 分类器必须以计算机可以处理的某种正式语言来表示。相对应的，为Leaner选择一个表示形式等同于选择它可能学习的一组分类器。该集合称为Leaner的假设空间。如果分类器不在假设空间中，则无法学习。我后面将讲到的一个相关问题是如何表示输入，换句话说，使用什么特征表示输入。
• Evaluation. An evaluation function (also called objective function or scoring function) is needed to distinguish good classifiers from bad ones. The evaluation function used internally by the algorithm may differ from the external one that we want the classifier to optimize, for ease of optimization and due to the issues I will discuss.
• 评估。 需要评估函数（也称为目标函数或评分函数）来区分良好的分类器和不良的分类器。该算法内部使用的评估函数可能与我们希望分类器优化的外部评估函数有所不同，这是为了简化优化以及由于我将要讨论的问题。
• Optimization. Finally, we need a method to search among the classifiers in the language for the highest-scoring one. The choice of optimization technique is key to the efficiency of the learner, and also helps determine the classifier produced if the evaluation function has more than one optimum. It is common for new learners to start out using off-the-shelf optimizers, which are later replaced by custom-designed ones.
• 优化。 最后，我们需要一种在语言中的分类器中搜索得分最高的方法。优化技术的选择是Leaner效率的关键，并且如果评估函数具有多个最优值，则还有助于确定生成的分类器。对于初学者来说，开始使用现成的优化器是很常见的，后来被定制设计的优化器所取代。

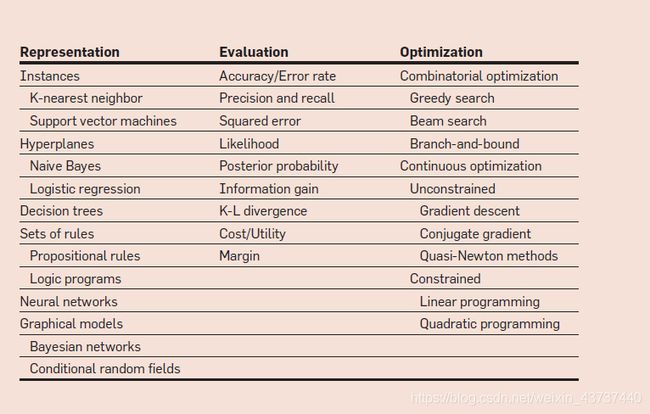
The accompanying table shows common examples of each of these three components. For example, k-nearest neighbor classifies a test example by finding the k most similar training examples and predicting the majority class among them. Hyperplane-based methods form a linear combination of the features per class and predict the class with the highest-valued combination. Decision trees test one feature at each internal node, with one branch for each feature value, and have class predictions at the leaves. Algorithm 1 (above) shows a bare-bones decision tree learner for Boolean domains, using information gain and greedy search. InfoGain(x_j, y) is the mutual information between feature x_j and the class y. MakeNode(x,c₀,c₁) returns a node that tests feature x and has c₀ as the child for x = 0 and c₁ as the child for x = 1.

下表显示了这三个组件中每个组件的通用示例。例如，KNN通过找到k个最相似的训练示例并预测其中的多数类来对测试示例进行分类。基于超平面的方法形成每个类别的特征的线性组合，并使用最高价值的组合预测类别。决策树在每个内部节点测试一个特征，每个特征值具有一个分支，并在叶子处进行类预测。上面的算法1显示了使用信息增益和贪婪搜索的布尔域的准决策树Learner。 InfoGain(x_j, y) 是特征 x_j与类y之间的相关信息。MakeNode(x,c₀,c₁)返回一个节点即测试设有X并且 c₀作为x = 0的子节点，c₁作为x = 1的子节点。

Of course, not all combinations of one component from each column of the table make equal sense. For example, discrete representations naturally go with combinatorial optimization, and continuous ones with continuous optimization. Nevertheless, many learners have both discrete and continuous components, and in fact the day may not be far when every single possible combination has appeared in some learner!

当然，并非表的每一列中的一个组件的所有组合都具有同等的意义。例如，离散表示自然会与组合优化一起使用，而连续表示则会与连续优化一起使用。但是，许多Leaner具有离散和连续的组成部分，实际上，可能不久就会在某些Leaner中出现每个可能的组合！

Most textbooks are organized by representation, and it is easy to over-look the fact that the other components are equally important. There is no simple recipe for choosing each component, but I will touch on some of the key issues here. As we will see, some choices in a machine learning project may be even more important than the choice of learner.

大多数教科书都是按表示形式组织的，很容易忽略其他组成部分同等重要的事实。没有一种简单方法指导你选择组件的组合，但是我将在这里讨论一些关键问题。正如我们将看到的，机器学习项目中的某些选择可能比Leaner的选择更为重要。

2. It’s Generalization that Counts / 概括才是最重要的

The fundamental goal of machine learning is to generalize beyond the examples in the training set. This is because, no matter how much data we have, it is very unlikely that we will see those exact examples again at test time. (Notice that, if there are 100,000 words in the dictionary, the spam filter described above has 2^100,000 possible different inputs.) Doing well on the training set is easy (just memorize the examples). The most common mistake among machine learning beginners is to test on the training data and have the illusion of success. If the chosen classifier is then tested on new data, it is often no better than random guessing. So, if you hire someone to build a classifier, be sure to keep some of the data to yourself and test the classifier they give you on it. Conversely, if you have been hired to build a classifier, set some of the data aside from the beginning, and only use it to test your chosen classifier at the very end, followed by learning your final classifier on the whole data.

机器学习的基本目标是对训练集中的示例进行概括。这是因为，无论我们拥有多少数据，我们都不太可能在测试时再次看到这些确切的示例。（请注意，如果词典中有100,000个单词，则上述垃圾邮件过滤器将有2^100,000个可能需要不同的输入。）在训练集上做得好很容易（仅记住所有示例）。在机器学习初学者中，最常见的错误是对训练集进行测试，并对成功抱有幻想。如果选择的分类器随后在新数据上进行测试，则通常不比随机猜测好。因此，如果您雇用某人来构建分类器，请确保将一些数据留给自己并测试他们在其中提供给您的分类器。相反，如果您被雇用来构建分类器，则从一开始就放置一些数据，并仅在最后使用它来测试所选分类器，然后学习整个数据的最终分类器。

Contamination of your classifier by test data can occur in insidious ways, for example, if you use test data to tune parameters and do a lot of tuning. (Machine learning algorithms have lots of knobs, and success often comes from twiddling them a lot, so this is a real concern.) Of course, holding out data reduces the amount available for training. This can be mitigated by doing cross-validation: randomly dividing your training data into (say) 10 subsets, holding out each one while training on the rest, testing each learned classifier on the examples it did not see, and averaging the results to see how well the particular parameter setting does.

测试数据对分类器的污染可能会以阴险的方式发生，例如，如果您使用测试数据来调整参数并进行大量调整。（机器学习算法有很多旋钮，而成功往往来自于对它们的大量调整，因此确实是一个需要考虑的问题。）当然，保留数据会减少可用于训练的数量。可以通过交叉验证来缓解这种情况：例如将训练数据随机分为10个子集，单独拿出每个子集并训练其余子集，最后在被拿出的子集上测试学习好的分类器，然后平均结果以查看特定参数设置的效果如何。

In the early days of machine learning, the need to keep training and test data separate was not widely appreciated. This was partly because, if the learner has a very limited representation (for example, hyperplanes), the difference between training and test error may not be large. But with very flexible classifiers (for example, decision trees), or even with linear classifiers with a lot of features, strict separation is mandatory.

在机器学习的早期，将培训和测试数据分开的需求并未得到广泛认可。部分原因是，如果Learner的表示形式非常有限（例如，超平面），则训练和测试错误之间的差异可能不会很大。但是，对于非常灵活的分类器（例如决策树），甚至对于具有很多特征的线性分类器，都必须进行严格的分隔。

Notice that generalization being the goal has an interesting consequence for machine learning. Unlike in most other optimization problems, we do not have access to the function we want to optimize! We have to use training error as a surrogate for test error, and this is fraught with danger. (How to deal with it is addressed later.) On the positive side, since the objective function is only a proxy for the true goal, we may not need to fully optimize it; in fact, a local optimum returned by simple greedy search may be better than the global optimum.

注意，将概括作为目标对于机器学习有一个有趣的结果。与大多数其他优化问题不同，我们无法访问要优化的函数！我们必须使用训练错误作为测试错误的替代，这充满了危险。（如何解决将在后面介绍。）积极的方面，由于目标函数只是真实目标的代理，因此，我们可能无需完全优化目标函数。实际上，通过简单的贪婪搜索返回的局部最优可能比全局最优更好。

3. Data Alone Is Not Enough / 只有数据是不够的

Generalization being the goal has another major consequence: Data alone is not enough, no matter how much of it you have. Consider learning a Boolean function of (say) 100 variables from a million examples. There are 2¹⁰⁰−10⁶ examples whose classes you do not know. How do you figure out what those classes are? In the absence of further information, there is just no way to do this that beats flipping a coin. This observation was first made (in somewhat different form) by the philosopher David Hume over 200 years ago, but even today many mistakes in machine learning stem from failing to appreciate it. Every learner must embody some knowledge or assumptions beyond the data it is given in order to generalize beyond it. This notion was formalized by Wolpert in his famous “no free lunch” theorems, according to which no learner can beat random guessing over all possible functions to be learned.25

将概括作为目标有另一个重要后果：只有数据是不够的，无论您拥有多少。假设考虑从一百万个示例中学习100个变量的布尔函数。有2¹⁰⁰−10⁶ 个您不知道其类型的示例。您如何弄清楚这些类是什么？在没有更多信息的情况下，没有办法做到比掷硬币还要好。这种观察是200多年前哲学家David Hume首次提出的（形式有所不同），但是直到今天，机器学习中的许多错误仍然源于对它的欣赏。每个Learner都必须在给出的数据之外体现一些知识或假设，以便对其进行概括。Wolpert在他著名的“无免费午餐” 定理中正式化了这一概念，根据该定理，没有Learner可以在所有可能的函数上胜过随机猜测 。 ⁴

This seems like rather depressing news. How then can we ever hope to learn anything? Luckily, the functions we want to learn in the real world are not drawn uniformly from the set of all mathematically possible functions! In fact, very general assumptions like smoothness, similar examples having similar classes, limited dependences, or limited complexityare often enough to do very well, and this is a large part of why machine learning has been so successful. Like deduction, induction (what learners do) is a knowledge lever: it turns a small amount of input knowledge into a large amount of output knowledge. Induction is a vastly more powerful lever than deduction, requiring much less input knowledge to produce useful results, but it still needs more than zero input knowledge to work. And, as with any lever, the more we put in, the more we can get out.

这似乎是令人沮丧的消息。那我们怎么能希望学到什么呢？幸运的是，我们想在现实世界中学习的函数并不是从所有数学上可能的函数集中统一得出！实际上，非常通用的假设，比如平滑度，相似的示例具有相似的类，有限依赖和有限复杂性通常足以很好地完成工作，这是机器学习如此成功的很大一部分原因。像演绎一样，归纳（Learner的工作方式）是知识的杠杆：它将少量的输入知识转变为大量的输出知识。归纳法比演绎法具有更强大的杠杆作用，更少的输入知识就可以产生有用的结果，但工作仍需要超过零的输入知识。而且，与任何杠杆一样，我们投入的越多，得到的越多。

A corollary of this is that one of the key criteria for choosing a representation is which kinds of knowledge are easily expressed in it. For example, if we have a lot of knowledge about what makes examples similar in our domain, instance-based methods may be a good choice. If we have knowledge about probabilistic dependencies, graphical models are a good fit. And if we have knowledge about what kinds of preconditions are required by each class, “IF … THEN …” rules may be the best option. The most useful learners in this regard are those that do not just have assumptions hardwired into them, but allow us to state them explicitly, vary them widely, and incorporate them automatically into the learning (for example, using first-order logic21 or grammars6).

必然的结果是，选择一种表示形式的关键标准之一就是哪些知识可以被它轻松表达。例如，如果我们了解什么使示例在我们的领域相似，那么基于实例的方法可能是一个不错的选择。如果我们了解概率依赖性，那么图模型非常适合。而且，如果我们了解每个类都需要什么样的前提条件，则 “ IF … THEN …”规则 可能是最佳选择。在这方面，最有用的Learner是那些不仅将假设扎根于其中的假设，而且使我们能够明确地陈述它们，进行大范围的变化并将它们自动并入学习中（例如，使用一阶逻辑21或语法6）。

In retrospect, the need for knowledge in learning should not be surprising. Machine learning is not magic; it cannot get something from nothing. What it does is get more from less. Programming, like all engineering, is a lot of work: we have to build everything from scratch. Learning is more like farming, which lets nature do most of the work. Farmers combine seeds with nutrients to grow crops. Learners combine knowledge with data to grow programs.

回想起来，学习中对知识的需求应该不足为奇。机器学习不是魔术。它不可能一事无成。它所做的就是事半功倍。像所有工程学一样，编程工作量很大：我们必须从头开始构建所有内容。学习更像是农业，它让自然完成大部分工作。农民将种子与养分结合起来种植农作物。Learner将知识与数据相结合以开发程序。

4. Overfitting Has Many Faces / 过拟合有多种形式

What if the knowledge and data we have are not sufficient to completely determine the correct classifier? Then we run the risk of just hallucinating a classifier (or parts of it) that is not grounded in reality, and is simply encoding random quirks in the data. This problem is called overfitting, and is the bugbear of machine learning. When your learner outputs a classifier that is 100% accurate on the training data but only 50% accurate on test data, when in fact it could have output one that is 75% accurate on both, it has overfit.

如果我们拥有的知识和数据不足以完全确定正确的分类器，该怎么办？我们有一定风险构造了假的的分类器（或分类器的一部分），这些分类器不真实，并且简单地编码了数据中的随机“怪胎”。这个问题称为过拟合，是机器学习的负担。当您的Learner输出的训练数据分类器的准确度为100％，而测试数据的分类器的准确度仅为50％时，实际上，当输出的分类器在两者的准确度为75％时，就显得过拟合了。

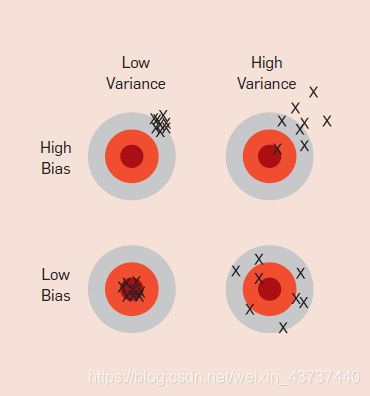
Everyone in machine learning knows about overfitting, but it comes in many forms that are not immediately obvious. One way to understand overfitting is by decomposing generalization error into bias and variance.9 Bias is a learner’s tendency to consistently learn the same wrong thing. Variance is the tendency to learn random things irrespective of the real signal. Figure 1 illustrates this by an analogy with throwing darts at a board. A linear learner has high bias, because when the frontier between two classes is not a hyperplane the learner is unable to induce it. Decision trees do not have this problem because they can represent any Boolean function, but on the other hand they can suffer from high variance: decision trees learned on different training sets generated by the same phenomenon are often very different, when in fact they should be the same. Similar reasoning applies to the choice of optimization method: beam search has lower bias than greedy search, but higher variance, because it tries more hypotheses. Thus, contrary to intuition, a more powerful learner is not necessarily better than a less powerful one.

机器学习中的每个人都知道过拟合，但是它以许多形式出现，但并不立即显而易见。一种理解过度拟合的方法是将泛化误差分解为偏差和差异 9。偏差是Learner不断学习同一错误事物的倾向。差异是学习随机事物的趋势，与真实信号无关。图1用在板上扔飞镖的类比说明了这一点。线性Learner具有较高的偏差，因为当两类之间的边界不是超平面时，Learner无法诱导它。决策树不存在此问题，因为它们可以表示任何布尔函数，但是另一方面，它们可能遭受高差异：在由相同现象生成的不同训练集上学习的决策树通常相差很大，而实际上它们应该是相同。类似的推断适用于优化方法的选择：波束搜索比贪婪搜索具有更低的偏差，但差异更大，因为它尝试了更多的假设。因此，与直觉相反，能力更强的Learner不一定比能力较弱的Learner更好。

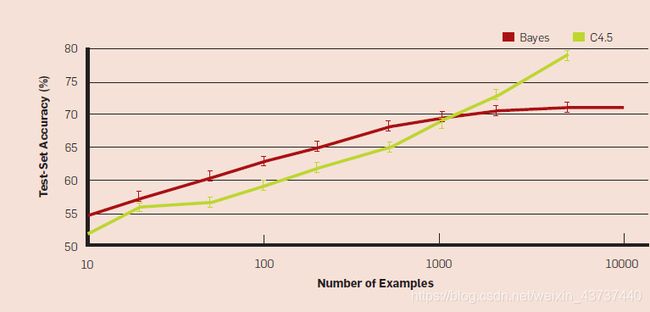
Figure 2 illustrates this.a Even though the true classifier is a set of rules, with up to 1,000 examples naive Bayes is more accurate than a rule learner. This happens despite naive Bayes’s false assumption that the frontier is linear! Situations like this are common in machine learning: strong false assumptions can be better than weak true ones, because a learner with the latter needs more data to avoid overfitting.

图2对此进行了说明。一个即使真正的分类是一组规则，具有高达1000点的例子朴素贝叶斯大于规则的Learner更准确。尽管朴素的贝叶斯错误地假设边界是线性的，但仍会发生这种情况！这样的情况在机器学习中很常见：强的错误假设可能比弱的真实假设更好，因为拥有后者的Learner需要更多数据来避免过拟合。

Cross-validation can help to combat overfitting, for example by using it to choose the best size of decision tree to learn. But it is no panacea, since if we use it to make too many parameter choices it can itself start to overfit.17

交叉验证可以帮助解决过度拟合问题，例如，通过使用交叉验证来选择要学习的最佳决策树大小。但这不是万能药，因为如果我们使用它进行过多的参数选择，它本身可能会开始过拟合。17

Besides cross-validation, there are many methods to combat overfitting. The most popular one is adding a regularization term to the evaluation function. This can, for example, penalize classifiers with more structure, thereby favoring smaller ones with less room to overfit. Another option is to perform a statistical significance test like chi-square before adding new structure, to decide whether the distribution of the class really is different with and without this structure. These techniques are particularly useful when data is very scarce. Nevertheless, you should be skeptical of claims that a particular technique “solves” the overfitting problem. It is easy to avoid overfitting (variance) by falling into the opposite error of underfitting (bias). Simultaneously avoiding both requires learning a perfect classifier, and short of knowing it in advance there is no single technique that will always do best (no free lunch).

除了交叉验证之外，还有许多方法可以防止过度拟合。最受欢迎的一种是添加正则项评估函数。例如，惩罚具有更多结构的分类器，从而倾向得到过拟合空间较小的分类器。另一种选择是在添加新结构之前执行统计显着性检验（例如卡方），以确定使用和不使用此结构时类的分布是否确实有所不同。当数据非常稀缺时，这些技术特别有用。但是，您应该对特定技术“解决”过拟合问题的说法持怀疑态度。避免过拟合（差异）很容易陷入欠拟合（偏差）。同时避免这两种情况都需要学习一个完美的分类器，而且由于事先不知道该分类器，所以没有一种技术会永远做到最好（没有免费的午餐）。

A common misconception about overfitting is that it is caused by noise, like training examples labeled with the wrong class. This can indeed aggravate overfitting, by making the learner draw a capricious frontier to keep those examples on what it thinks is the right side. But severe overfitting can occur even in the absence of noise. For instance, suppose we learn a Boolean classifier that is just the disjunction of the examples labeled “true” in the training set. (In other words, the classifier is a Boolean formula in disjunctive normal form, where each term is the conjunction of the feature values of one specific training example.) This classifier gets all the training examples right and every positive test example wrong, regardless of whether the training data is noisy or not.

关于过度拟合的一个常见误解是它是由噪声引起的，例如带有错误类的训练示例。通过使Learner画出一个反复无常的疆界以使这些示例停留在它认为正确的一面，确实可以加剧过拟合。但是，即使没有噪音，也可能发生严重的过拟合。例如，假设我们学习了一个布尔分类器，它只是训练集中标记为“ true”的示例的分离。（换句话说，分类器就是一个析取形式的公式，其中每个项都是一个特定训练示例的特征值的并集。）该分类器对所有训练示例正确，但是对每个积极测试示例错误，无论训练数据是否嘈杂。

The problem of multiple testing13 is closely related to overfitting. Standard statistical tests assume that only one hypothesis is being tested, but modern learners can easily test millions before they are done. As a result what looks significant may in fact not be. For example, a mutual fund that beats the market 10 years in a row looks very impressive, until you realize that, if there are 1,000 funds and each has a 50% chance of beating the market on any given year, it is quite likely that one will succeed all 10 times just by luck. This problem can be combatted by correcting the significance tests to take the number of hypotheses into account, but this can also lead to underfitting. A better approach is to control the fraction of falsely accepted non-null hypotheses, known as the false discovery rate.3

多次测试的问题13与过度拟合密切相关。标准的统计检验假设只对一种假设进行检验，但是现代Learner可以轻松地完成数百万的检验。结果，看起来重要的实际上可能不是。例如，一个连续十年打败市场的共同基金看起来非常令人印象深刻，直到您意识到，如果有1,000只基金，并且每种基金在任何一年都有击败市场的机会达到50％，那么很有可能仅仅靠运气，一个人就能成功十次。可以通过校正重要性检验以考虑假设的数量来解决此问题，但这也可能导致拟合不足。更好的方法是控制错误接受的非零假设的比例，即错误发现率。3

5. Intuition Fails in High Dimensions / 在高维度中直觉失效

After overfitting, the biggest problem in machine learning is the curse of dimensionality. This expression was coined by Bellman in 1961 to refer to the fact that many algorithms that work fine in low dimensions become intractable when the input is high-dimensional. But in machine learning it refers to much more. Generalizing correctly becomes exponentially harder as the dimensionality (number of features) of the examples grows, because a fixed-size training set covers a dwindling fraction of the input space. Even with a moderate dimension of 100 and a huge training set of a trillion examples, the latter covers only a fraction of about 10−18 of the input space. This is what makes machine learning both necessary and hard.

经过过度拟合后，机器学习中的最大问题是维数的诅咒。此表达由Bellman在1961年创造，指的是当输入为高维时，许多在低维上运行良好的算法变得难以处理的事实。但是在机器学习中，它涉及的更多。随着示例维数（特征数量）的增长，正确归纳变得越来越困难，因为固定大小的训练集覆盖了输入空间的不断缩小的部分。即使具有100的适度维度和数以万亿计的示例的庞大训练集，后者也仅覆盖了约10^-18的输入空间的一小部分。这就是使机器学习既必要又困难的原因。

More seriously, the similarity-based reasoning that machine learning algorithms depend on (explicitly or implicitly) breaks down in high dimensions. Consider a nearest neighbor classifier with Hamming distance as the similarity measure, and suppose the class is just x1 and x2. If there are no other features, this is an easy problem. But if there are 98 irrelevant features x3,…, x100, the noise from them completely swamps the signal in x1 and x2, and nearest neighbor effectively makes random predictions.

更严重的是，机器学习算法所依赖的基于相似性的推理（显式或隐式）在高维度上分解。将具有Hamming距离的最近邻居作为相似性度量，并假设该类仅为x₁ and x₂。如果没有其他功能，这是一个简单的问题。但是，如果存在98个不相关的特征x₃，…，x₁₀₀，则来自它们的噪声将x₁和x₂中的信号完全淹没，并且最近邻居会有效地进行随机预测。

Even more disturbing is that nearest neighbor still has a problem even if all 100 features are relevant! This is because in high dimensions all examples look alike. Suppose, for instance, that examples are laid out on a regular grid, and consider a test example x_t. If the grid is d-dimensional, x_t’s 2d nearest examples are all at the same distance from it. So as the dimensionality increases, more and more examples become nearest neighbors of x_t, until the choice of nearest neighbor (and therefore of class) is effectively random.

更令人不安的是，即使所有100个功能都相关，最近的邻居仍然有问题！这是因为在高维度上，所有示例都相似。例如，假设将示例放置在规则的网格上，并考虑一个测试示例x_t。如果网格是d维的，则x_t的2d个最近的示例都与网格距离相同。因此，随着维数的增加，越来越多的示例成为x_t的最接近邻居，直到最接近邻居（以及类别）的选择实际上是随机的。

This is only one instance of a more general problem with high dimensions: our intuitions, which come from a three-dimensional world, often do not apply in high-dimensional ones. In high dimensions, most of the mass of a multivariate Gaussian distribution is not near the mean, but in an increasingly distant “shell” around it; and most of the volume of a high-dimensional orange is in the skin, not the pulp. If a constant number of examples is distributed uniformly in a high-dimensional hypercube, beyond some dimensionality most examples are closer to a face of the hypercube than to their nearest neighbor. And if we approximate a hypersphere by inscribing it in a hypercube, in high dimensions almost all the volume of the hypercube is outside the hypersphere. This is bad news for machine learning, where shapes of one type are often approximated by shapes of another.

这只是高维一个更普遍的问题的一个例子：我们的直觉来自三维世界，通常不适用于高维世界。在高维中，多元高斯分布的大部分质量都不在均值附近，而是在它周围越来越远的“壳”中。高维橙的大部分体积在皮肤中，而不是果肉中。如果恒定数量的示例均匀分布在高维超立方体中，则除了某些维度之外，大多数示例更接近于超立方体的面而不是其最近邻居。而且，如果我们通过将超球体刻在超立方体中来近似一个超球体，那么在高维度上，几乎所有超立方体的体积都在超球体之外。其中一种类型的形状通常由另一种形状近似，这对机器学习来说是个坏消息。

Building a classifier in two or three dimensions is easy; we can find a reasonable frontier between examples of different classes just by visual inspection. (It has even been said that if people could see in high dimensions machine learning would not be necessary.) But in high dimensions it is difficult to understand what is happening. This in turn makes it difficult to design a good classifier. Naively, one might think that gathering more features never hurts, since at worst they provide no new information about the class. But in fact their benefits may be outweighed by the curse of dimensionality.

在二维或三个维度上建立分类器很容易；仅通过视觉检查，我们就可以在不同类别的示例之间找到合理的边界。（甚至有人说，如果人们可以在高维度上看到机器学习就没有必要了。）但是在高维度上，很难理解正在发生的事情。反过来，这使得设计好的分类器变得困难。天真的，人们可能会认为收集更多功能永远不会有伤害，因为在最坏的情况下，它们不提供有关该类的新信息。但是实际上，它们的好处可能会因维数的诅咒而被抵消。

Fortunately, there is an effect that partly counteracts the curse, which might be called the “blessing of non-uniformity.” In most applications examples are not spread uniformly throughout the instance space, but are concentrated on or near a lower-dimensional manifold. For example, k-nearest neighbor works quite well for handwritten digit recognition even though images of digits have one dimension per pixel, because the space of digit images is much smaller than the space of all possible images. Learners can implicitly take advantage of this lower effective dimension, or algorithms for explicitly reducing the dimensionality can be used (for example, Tenenbaum22).

幸运的是，有一种效果可以部分抵消这种诅咒，这可能被称为“祝福非均匀性”。在大多数应用中，示例并非均匀分布在整个实例空间中，而是集中在低维流形上或附近。例如，即使数字图像每像素具有一维，k近邻也可以很好地用于手写数字识别，因为数字图像的空间远小于所有可能图像的空间。Learner可以隐式地利用这个较低的有效维度，或者可以使用显式降低维度的算法（例如Tenenbaum 22）。

6. Theoretical Guarantees Are Not What They Seem / 理论保证并非它们看起来那样

Machine learning papers are full of theoretical guarantees. The most common type is a bound on the number of examples needed to ensure good generalization. What should you make of these guarantees? First of all, it is remarkable that they are even possible. Induction is traditionally contrasted with deduction: in deduction you can guarantee that the conclusions are correct; in induction all bets are off. Or such was the conventional wisdom for many centuries. One of the major developments of recent decades has been the realization that in fact we can have guarantees on the results of induction, particularly if we are willing to settle for probabilistic guarantees.

机器学习论文充满了理论保证。最常见的类型是确保良好概括所需的示例数量的界限。您应该怎么做这些保证？首先，值得注意的是，它们甚至是可能的。传统上，归纳法与演绎法形成对比：在演绎中，您可以保证结论是正确的；归纳并不行。多个世纪以来的传统智慧就是如此。近几十年来的主要发展之一是认识到实际上我们可以对归纳的结果提供保证，特别是如果我们愿意作概率保证。

The basic argument is remarkably simple⁵. Let’s say a classifier is bad if its true error rate is greater than ε. Then the probability that a bad classifier is consistent with n random, independent training examples is less than (1-ε)ⁿ. Let b be the number of bad classifiers in the learner’s hypothesis space H. The probability that at least one of them is consistent is less than b(1-ε)ⁿ, by the union bound. Assuming the learner always returns a consistent classifier, the probability that this classifier is bad is then less than |H|(1-ε)ⁿ, where we have used the fact that b ≤ |H|. So if we want this probability to be less than δ, it suffices to make n > ln(δ/|H|)/ ln(1-ε) ≥ 1/ε(ln |H| + ln 1/δ).

基本论点非常简单⁵。假设分类器的真实错误率大于ε，则它是错误的。那么，不良分类器与n个随机独立训练示例一致的概率小于(1-ε)ⁿ。令b为Learner假设空间H中不良分类器的数量。通过联合约束，它们中至少一个是一致的概率小于b(1-ε)ⁿ。假设Learner总是返回一个一致的分​​类器，则该分类器不良的概率小于|H|(1-ε)ⁿ，在这里我们使用的事实，b ≤| H |。因此，如果我们希望该概率小于δ，则足以使n > ln(δ/ |H|)/ ln(1-ε）≥1 /ε(ln|H| + ln 1 /δ)。

Unfortunately, guarantees of this type have to be taken with a large grain of salt. This is because the bounds obtained in this way are usually extremely loose. The wonderful feature of the bound above is that the required number of examples only grows logarithmically with |H| and 1/δ. Unfortunately, most interesting hypothesis spaces are doubly exponential in the number of features d, which still leaves us needing a number of examples exponential in d. For example, consider the space of Boolean functions of d Boolean variables. If there are e possible different examples, there are 2e possible different functions, so since there are 2d possible examples, the total number of functions is 22d. And even for hypothesis spaces that are “merely” exponential, the bound is still very loose, because the union bound is very pessimistic. For example, if there are 100 Boolean features and the hypothesis space is decision trees with up to 10 levels, to guarantee δ = ε = 1% in the bound above we need half a million examples. But in practice a small fraction of this suffices for accurate learning.

不幸的是，这种保证必须与大颗粒的盐一起使用。这是因为以这种方式获得的边界通常非常松散。上界的妙处在于，所需的示例数仅与|H| 和1 /δ成对数增长。不幸的是，最有趣的假设空间在特征d的数量上是双指数的，这仍然使我们需要在d中使用指数的实例。例如，考虑d个布尔变量的布尔函数的空间。如果有e个不同的示例，则有2个e可能有不同的函数，因此有2个d可能的示例，功能总数为22d。甚至对于“仅”指数空间的假设空间，边界仍然非常宽松，因为联合边界非常悲观。例如，如果有100个布尔特征，并且假设空间是最多10个级别的决策树，则要保证上面的范围内δ= ε= 1％，我们需要50万个示例。但是实际上，其中的一小部分就足以进行准确的学习。

Further, we have to be careful about what a bound like this means. For instance, it does not say that, if your learner returned a hypothesis consistent with a particular training set, then this hypothesis probably generalizes well. What it says is that, given a large enough training set, with high probability your learner will either return a hypothesis that generalizes well or be unable to find a consistent hypothesis. The bound also says nothing about how to select a good hypothesis space. It only tells us that, if the hypothesis space contains the true classifier, then the probability that the learner outputs a bad classifier decreases with training set size. If we shrink the hypothesis space, the bound improves, but the chances that it contains the true classifier shrink also. (There are bounds for the case where the true classifier is not in the hypothesis space, but similar considerations apply to them.)

此外，我们必须小心这种界限的含义。例如，它并不是说，如果您的Learner返回了与特定训练集一致的假设，那么该假设可能会很好地推广。它的意思是，在给定足够大的训练集的情况下，您的Learner很有可能会返回普遍性很好的假设，或者无法找到一致的假设。边界也没有说明如何选择一个好的假设空间。它仅告诉我们，如果假设空间包含真实分类器，则Learner输出不良分类器的概率会随着训练集大小的增加而降低。如果缩小假设空间，边界会改善，但是包含真实分类器的机会也会缩小。

Another common type of theoretical guarantee is asymptotic: given infinite data, the learner is guaranteed to output the correct classifier. This is reassuring, but it would be rash to choose one learner over another because of its asymptotic guarantees. In practice, we are seldom in the asymptotic regime (also known as “asymptopia”). And, because of the bias-variance trade-off I discussed earlier, if learner A is better than learner B given infinite data, B is often better than A given finite data.

理论保证的另一种常见类型是渐进：给定无限数据，保证Learner输出正确的分类器。这令人放心，但是由于其渐近性保证，选择一个Learner而不是另一个Learner将是轻率的。实际上，我们很少处于渐近状态（也称为“渐近”）。而且，由于我前面讨论了偏差-方差的折衷，如果LearnerA在给定无限数据的情况下优于LearnerB，则在给定有限数据的情况下B通常优于LearnerB。

The main role of theoretical guarantees in machine learning is not as a criterion for practical decisions, but as a source of understanding and driving force for algorithm design. In this capacity, they are quite useful; indeed, the close interplay of theory and practice is one of the main reasons machine learning has made so much progress over the years. But caveat emptor: learning is a complex phenomenon, and just because a learner has a theoretical justification and works in practice does not mean the former is the reason for the latter.

理论保证在机器学习中的主要作用不是作为实际决策的标准，而是作为算法设计的理解和驱动力的来源。以这种身份，它们非常有用；确实，理论与实践之间的紧密互动是机器学习多年来取得如此巨大进步的主要原因之一。但是，告诫者：学习是一个复杂的现象，仅仅因为Learner具有理论上的合理性并在实践中工作并不意味着前者是后者的原因。

7. Feature Engineering Is The Key / 特征工程是关键

At the end of the day, some machine learning projects succeed and some fail. What makes the difference? Easily the most important factor is the features used. Learning is easy if you have many independent features that each correlate well with the class. On the other hand, if the class is a very complex function of the features, you may not be able to learn it. Often, the raw data is not in a form that is amenable to learning, but you can construct features from it that are. This is typically where most of the effort in a machine learning project goes. It is often also one of the most interesting parts, where intuition, creativity and “black art” are as important as the technical stuff.

最终，一些机器学习项目成功了，而有些失败了。有什么区别？最重要的因素就是所使用的特征。如果您具有许多与类紧密相关的独立功能，则学习将很容易。另一方面，如果类是特征的非常复杂的函数，则可能无法学习。通常，原始数据的格式不适合学习，但您可以从中构造特征。这是机器学习项目中大部分工作的去向。它通常也是最有趣的部分之一，直觉，创造力和“妖术”与技术同样重要。

First-timers are often surprised by how little time in a machine learning project is spent actually doing machine learning. But it makes sense if you consider how time-consuming it is to gather data, integrate it, clean it and preprocess it, and how much trial and error can go into feature design. Also, machine learning is not a one-shot process of building a dataset and running a learner, but rather an iterative process of running the learner, analyzing the results, modifying the data and/or the learner, and repeating. Learning is often the quickest part of this, but that is because we have already mastered it pretty well! Feature engineering is more difficult because it is domain-specific, while learners can be largely general purpose. However, there is no sharp frontier between the two, and this is another reason the most useful learners are those that facilitate incorporating knowledge.

初学者通常会对在机器学习项目中实际花费很少的时间进行机器学习感到惊讶。但是，如果您考虑数据收集，整合，清理和预处理要花费多长时间，以及在功能设计中可以进行多少试验和尝试，这是有道理的。而且，机器学习不是构建数据集和运行Learner的一站式过程，而是运行Learner，分析结果，修改数据或Learner并重复的迭代过程。学习通常是最快的部分，但这是因为我们已经很好地掌握了它！特征工程更加困难，因为它是特定于领域的，而Learner在很大程度上可能是通用的。但是，两者之间没有明确的边界。

Of course, one of the holy grails of machine learning is to automate more and more of the feature engineering process. One way this is often done today is by automatically generating large numbers of candidate features and selecting the best by (say) their information gain with respect to the class. But bear in mind that features that look irrelevant in isolation may be relevant in combination. For example, if the class is an XOR of k input features, each of them by itself carries no information about the class. (If you want to annoy machine learners, bring up XOR.) On the other hand, running a learner with a very large number of features to find out which ones are useful in combination may be too time-consuming, or cause overfitting. So there is ultimately no replacement for the smarts you put into feature engineering.

当然，机器学习的圣杯之一就是使越来越多的特征工程过程自动化。今天通常这样做的一种方式是通过自动生成大量候选特征并通过（例如说）它们相对于类别的信息增益来选择最佳特征。但是请记住，孤立地看起来不相关的功能可能会组合在一起使用。例如，如果该类是k的XOR输入功能，每个功能本身都不包含有关类的信息。（如果您想让机器Learner感到烦恼，请提出XOR。）另一方面，运行具有大量功能的Learner以找出哪些功能可以组合使用可能会非常耗时，或者导致过拟合。因此，最终您无法替代投入功能工程的智能设备。

8. More Data Beats a Cleverer Algorithm / 更多数据胜过更聪明的算法

Suppose you have constructed the best set of features you can, but the classifiers you receive are still not accurate enough. What can you do now? There are two main choices: design a better learning algorithm, or gather more data (more examples, and possibly more raw features, subject to the curse of dimensionality). Machine learning researchers are mainly concerned with the former, but pragmatically the quickest path to success is often to just get more data. As a rule of thumb, a dumb algorithm with lots and lots of data beats a clever one with modest amounts of it. (After all, machine learning is all about letting data do the heavy lifting.)

假设您已经构建了最好的功能集，但是收到的分类器仍然不够准确。你现在可以做什么？有两个主要选择：设计更好的学习算法，或收集更多数据（更多示例，可能还有更多原始特征，这取决于维度的诅咒）。机器学习研究人员主要关注前者，但实用的是，成功的最快途径通常是获取更多数据。根据经验，具有大量数据的愚蠢算法会击败数量适中的聪明算法。（毕竟，机器学习只不过是让数据承担繁重的工作。）

This does bring up another problem, however: scalability. In most of computer science, the two main limited resources are time and memory. In machine learning, there is a third one: training data. Which one is the bottleneck has changed from decade to decade. In the 1980s it tended to be data. Today it is often time. Enormous mountains of data are available, but there is not enough time to process it, so it goes unused. This leads to a paradox: even though in principle more data means that more complex classifiers can be learned, in practice simpler classifiers wind up being used, because complex ones take too long to learn. Part of the answer is to come up with fast ways to learn complex classifiers, and indeed there has been remarkable progress in this direction (for example, Hulten and Domingos11).

但是，这确实带来了另一个问题：可伸缩性。在大多数计算机科学中，两个主要的有限资源是时间和内存。在机器学习中，有第三个：训练数据。哪个是瓶颈在不同的十年里是不同的。在1980年代，它往往是数据。如今有大量可以使用的数据，但是没有足够的时间来处理它，因此它无法使用。这导致了一个悖论：即使原则上更多的数据意味着可以学习更复杂的分类器，但实际上会使用更简单的分类器，因为复杂的分类器学习时间太长。答案的一部分是想出一种学习复杂分类器的快速方法，并且确实在这个方向上已经取得了显著进步（例如，Hulten和Domingos 11）。

Part of the reason using cleverer algorithms has a smaller payoff than you might expect is that, to a first approximation, they all do the same. This is surprising when you consider representations as different as, say, sets of rules and neural networks. But in fact propositional rules are readily encoded as neural networks, and similar relationships hold between other representations. All learners essentially work by grouping nearby examples into the same class; the key difference is in the meaning of “nearby.” With nonuniformly distributed data, learners can produce widely different frontiers while still making the same predictions in the regions that matter (those with a substantial number of training examples, and therefore also where most test examples are likely to appear). This also helps explain why powerful learners can be unstable but still accurate. Figure 3 illustrates this in 2D; the effect is much stronger in high dimensions.

使用更聪明的算法获得的收益比您预期的要小的部分原因是，从一阶近似值来看，它们都做同样的事情。当您认为表示形式与规则集和神经网络不同时，这令人惊讶。但是实际上，命题规则很容易被编码为神经网络，并且其他表示之间也存在类似的关系。本质上，所有Learner都将附近的示例分组到同一个类中进行学习；关键区别在于“附近”的含义。使用非均匀分布的数据，Learner可以产生非常不同的边界，同时仍可以在重要区域做出相同的预测（那些区域具有大量的训练示例，因此也可能出现大多数测试示例）。图3以二维方式说明了这一点。在高维度时效果更强。

As a rule, it pays to try the simplest learners first (for example, naïve Bayes before logistic regression, k-nearest neighbor before support vector machines). More sophisticated learners are seductive, but they are usually harder to use, because they have more knobs you need to turn to get good results, and because their internals are more opaque.

通常，首先尝试最简单的Learner（例如，朴素贝叶斯先于逻辑回归，KNN先于SVM）是值得的。经验丰富的Learner会很诱人，但通常更难使用，因为他们需要转动更多的旋钮才能获得良好的效果，并且内部结构更加不透明。

Learners can be divided into two major types: those whose representation has a fixed size, like linear classifiers, and those whose representation can grow with the data, like decision trees. (The latter are sometimes called nonparametric learners, but this is somewhat unfortunate, since they usually wind up learning many more parameters than parametric ones.) Fixed-size learners can only take advantage of so much data. (Notice how the accuracy of naive Bayes asymptotes at around 70% in Figure 2.) Variable-size learners can in principle learn any function given sufficient data, but in practice they may not, because of limitations of the algorithm (for example, greedy search falls into local optima) or computational cost. Also, because of the curse of dimensionality, no existing amount of data may be enough. For these reasons, clever algorithmsthose that make the most of the data and computing resources availableoften pay off in the end, provided you are willing to put in the effort. There is no sharp frontier between designing learners and learning classifiers; rather, any given piece of knowledge could be encoded in the learner or learned from data. So machine learning projects often wind up having a significant component of learner design, and practitioners need to have some expertise in it.12

Learner可分为两种主要类型：那些具有固定大小的表示形式（如线性分类器）和那些随数据增长的表示形式（如决策树）。（后者有时称为非参数Learner，但这有点不幸，因为它们通常比参数学习更多的参数。）固定大小的Learner只能利用大量数据。（请注意，图2中朴素的贝叶斯渐近线的准确度如何达到70％左右。）可变大小的Learner原则上可以在给定足够数据的情况下学习任何函数，但实际上，由于算法的局限性（例如，贪婪搜索属于局部最优）或计算成本，他们可能无法学习任何函数。同样，由于维数的诅咒，现有数据量可能不足。由于这些原因，只要您愿意付出努力，那些可以充分利用可用数据和计算资源的聪明算法通常会在最后得到回报。在设计Learner和学习分类器之间没有明显的界限。相反，任何给定的知识都可以在Learner中编码或从数据中学习。因此，机器学习项目经常会成为Learner设计的重要组成部分，而从业者也需要具备一些专业知识。12

In the end, the biggest bottleneck is not data or CPU cycles, but human cycles. In research papers, learners are typically compared on measures of accuracy and computational cost. But human effort saved and insight gained, although harder to measure, are often more important. This favors learners that produce human-understandable output (for example, rule sets). And the organizations that make the most of machine learning are those that have in place an infrastructure that makes experimenting with many different learners, data sources, and learning problems easy and efficient, and where there is a close collaboration between machine learning experts and application domain ones.

最后，最大的瓶颈不是数据或CPU周期，而是人员周期。在研究论文中，通常会比较Learner的准确性和计算成本。但是，节省下来的精力和获得的洞察力虽然更难衡量，但通常更重要。这有利于产生人类可理解的输出（例如，规则集）的Learner。充分利用机器学习的组织是拥有适当基础设施的组织，这些基础设施使对许多不同的Learner，数据源和学习问题的尝试变得容易而高效，并且机器学习专家和应用程序领域之间有着密切的协作那些。

9. Learn Many Models, Not Just One / 学习多种模型，而不仅仅是一种

In the early days of machine learning, everyone had a favorite learner, together with some a priori reasons to believe in its superiority. Most effort went into trying many variations of it and selecting the best one. Then systematic empirical comparisons showed that the best learner varies from application to application, and systems containing many different learners started to appear. Effort now went into trying many variations of many learners, and still selecting just the best one. But then researchers noticed that, if instead of selecting the best variation found, we combine many variations, the results are betteroften much betterand at little extra effort for the user.

在机器学习的早期，每个人都有一个喜欢的Learner，还有一些先验的理由相信它的优越性。最大的努力是尝试多种变体并选择最佳的变体。然后，系统的经验比较表明，最佳Learner因应用程序而异，并且包含许多不同Learner的系统开始出现。现在，我们尝试了许多Learner的多种变体，并且仍然只选择最好的一种。但是随后研究人员注意到，如果不选择发现的最佳变体，而是结合许多变体，结果通常会更好得多，并且用户无需付出额外的努力。

Creating such model ensembles is now standard.1 In the simplest technique, called bagging, we simply generate random variations of the training set by resampling, learn a classifier on each, and combine the results by voting. This works because it greatly reduces variance while only slightly increasing bias. In boosting, training examples have weights, and these are varied so that each new classifier focuses on the examples the previous ones tended to get wrong. In stacking, the outputs of individual classifiers become the inputs of a “higher-level” learner that figures out how best to combine them.

创建这样的模型合奏现在是标准的。1在最简单的技术（称为bagging）中，我们仅需通过重采样就可以随机生成训练集的变体，学习每种训练器的分类器，然后通过投票将结果合并。之所以有效，是因为它大大减少了方差，同时仅稍微增加了偏差。在提升中，训练示例具有权重，并且权重各不相同，因此每个新的分类器都将重点放在以前的示例容易出错的示例上。在堆叠中，各个分类器的输出成为“高级”Learner的输入，该Learner找出如何最佳地组合它们。

Many other techniques exist, and the trend is toward larger and larger ensembles. In the Netflix prize, teams from all over the world competed to build the best video recommender system (http://netflixprize.com). As the competition progressed, teams found they obtained the best results by combining their learners with other teams’, and merged into larger and larger teams. The winner and runner-up were both stacked ensembles of over 100 learners, and combining the two ensembles further improved the results. Doubtless we will see even larger ones in the future.

存在许多其他技术，并且趋势是越来越大的合奏。在Netflix奖中，来自世界各地的团队竞争建立了最佳的视频推荐系统（http://netflixprize.com）。随着比赛的进行，团队发现他们通过将Learner与其他团队相结合而获得了最佳成绩，并合并为越来越大的团队。冠军和亚军都是超过100名Learner的堆叠乐团，将这两个乐团结合起来可以进一步提高成绩。毫无疑问，将来我们会看到更大的。

Model ensembles should not be confused with Bayesian model averaging (BMA)the theoretically optimal approach to learning.4 In BMA, predictions on new examples are made by averaging the individual predictions of all classifiers in the hypothesis space, weighted by how well the classifiers explain the training data and how much we believe in them a priori. Despite their superficial similarities, ensembles and BMA are very different. Ensembles change the hypothesis space (for example, from single decision trees to linear combinations of them), and can take a wide variety of forms. BMA assigns weights to the hypotheses in the original space according to a fixed formula. BMA weights are extremely different from those produced by (say) bagging or boosting: the latter are fairly even, while the former are extremely skewed, to the point where the single highest-weight classifier usually dominates, making BMA effectively equivalent to just selecting it.8 A practical consequence of this is that, while model ensembles are a key part of the machine learning toolkit, BMA is seldom worth the trouble.

模型集成不应与贝叶斯模型平均（BMA）（理论上最佳的学习方法）相混淆。4在BMA中，对新示例的预测是通过平均所有假设空间中的分类器，由分类器对训练数据的解释程度以及我们对它们的先验信任程度加权得出。尽管它们在表面上有相似之处，但乐团和BMA却大不相同。集成改变了假设空间（例如，从单个决策树变为线性决策组合），并且可以采用多种形式。BMA根据固定公式为原始空间中的假设分配权重。BMA权重与（例如）套袋或增强产生的权重完全不同：后者相当均匀，而前者则非常偏斜，以至于单个最高权重的分类器通常占主导地位，这使得BMA实际上等同于仅选择它。8 这样的实际结果是，虽然模型集成是机器学习工具包的关键部分，但BMA很少值得为此烦恼。

10. Simplicity Does Not Imply Accuracy / 简单并不意味着准确性

Occam’s razor famously states that entities should not be multiplied beyond necessity. In machine learning, this is often taken to mean that, given two classifiers with the same training error, the simpler of the two will likely have the lowest test error. Purported proofs of this claim appear regularly in the literature, but in fact there are many counterexamples to it, and the “no free lunch” theorems imply it cannot be true.

著名的奥卡姆剃刀指出，不应将实体复制到不必要的数量。在机器学习中，这通常是指给定两个具有相同训练误差的分类器，这两个分类器中较简单的一个可能具有最低的测试误差。有关此主张的声称证据定期出现在文献中，但实际上有许多反例，“无免费午餐”定理暗示此说法不成立。

We saw one counterexample previously: model ensembles. The generalization error of a boosted ensemble continues to improve by adding classifiers even after the training error has reached zero. Another counterexample is support vector machines, which can effectively have an infinite number of parameters without overfitting. Conversely, the function sign(sin(ax)) can discriminate an arbitrarily large, arbitrarily labeled set of points on the x axis, even though it has only one parameter.23 Thus, contrary to intuition, there is no necessary connection between the number of parameters of a model and its tendency to overfit.

之前我们看到了一个反例：模型集成。即使在训练误差达到零之后，通过添加分类器，增强的集成体的泛化误差也会继续改善。另一个反例是支持向量机，它可以有效地具有无限数量的参数而不会过度拟合。相反，功能符号（sin（ax））可以区分x轴上任意大的，标注标签的点集，即使它只有一个参数。23因此，与直觉相反，模型的参数数量与其过拟合趋势之间没有必要的联系。

A more sophisticated view instead equates complexity with the size of the hypothesis space, on the basis that smaller spaces allow hypotheses to be represented by shorter codes. Bounds like the one in the section on theoretical guarantees might then be viewed as implying that shorter hypotheses generalize better. This can be further refined by assigning shorter codes to the hypotheses in the space we have some a priori preference for. But viewing this as “proof” of a trade-off between accuracy and simplicity is circular reasoning: we made the hypotheses we prefer simpler by design, and if they are accurate it is because our preferences are accurate, not because the hypotheses are “simple” in the representation we chose.

相反，在较小的空间允许用较短的代码表示假设的基础上，更复杂的视图将复杂度与假设空间的大小等同起来。像理论保证一节中所述的界限可能被认为暗示着较短的假设可以更好地推广。通过为我们有一些先验偏好的空间中的假设分配较短的代码，可以进一步完善这一点。但是，将其视为在准确性和简单性之间进行折衷的“证明”是循环推理：我们通过设计使我们更喜欢的假设变得更简单，如果它们是准确的，那是因为我们的偏好是正确的，而不是因为假设是“简单的”在我们选择的表示形式中。

A further complication arises from the fact that few learners search their hypothesis space exhaustively. A learner with a larger hypothesis space that tries fewer hypotheses from it is less likely to overfit than one that tries more hypotheses from a smaller space. As Pearl18 points out, the size of the hypothesis space is only a rough guide to what really matters for relating training and test error: the procedure by which a hypothesis is chosen.

进一步的复杂性是由于几乎没有Learner详尽地搜索其假设空间这一事实引起的。与从较小空间尝试更多假设的学生相比，拥有较大假设空间的Learner从中尝试较少假设的可能性较小。正如Pearl 18指出的那样，假设空间的大小仅是对与训练和测试错误相关的真正重要内容的粗略指导：选择假设的过程。

Domingos7 surveys the main arguments and evidence on the issue of Occam’s razor in machine learning. The conclusion is that simpler hypotheses should be preferred because simplicity is a virtue in its own right, not because of a hypothetical connection with accuracy. This is probably what Occam meant in the first place.

Domingos 7调查了有关奥卡姆剃刀在机器学习中的问题的主要论据和证据。结论是，应该采用更简单的假设，因为简单本身就是一种美德，而不是因为假设与准确性之间存在联系。这可能是Occam首先的意思。

11. Representable Does Not Imply Learnable / 可表示并不意味着可学

Essentially all representations used in variable-size learners have associated theorems of the form “Every function can be represented, or approximated arbitrarily closely, using this representation.” Reassured by this, fans of the representation often proceed to ignore all others. However, just because a function can be represented does not mean it can be learned. For example, standard decision tree learners cannot learn trees with more leaves than there are training examples. In continuous spaces, representing even simple functions using a fixed set of primitives often requires an infinite number of components. Further, if the hypothesis space has many local optima of the evaluation function, as is often the case, the learner may not find the true function even if it is representable. Given finite data, time and memory, standard learners can learn only a tiny subset of all possible functions, and these subsets are different for learners with different representations. Therefore the key question is not “Can it be represented?” to which the answer is often trivial, but “Can it be learned?” And it pays to try different learners (and possibly combine them).

基本上，可变大小Learner中使用的所有表示形式都有相关的定理，形式为“使用该表示形式，每个函数都可以表示或任意近似地近似表示”。对此感到放心的是，代表制的拥护者经常会忽略其他所有人。但是，仅仅表示一个函数并不意味着可以学习它。例如，标准决策树Learner学习的叶子不能多于训练示例。在连续空间中，使用一组固定的基元表示即使是简单的函数，通常也需要无限数量的组件。此外，如果假设空间具有很多评估函数的局部最优值（如通常情况），则Learner即使找到可表示的真实函数也可能找不到。给定有限的数据，时间和内存，标准Learner只能学习所有可能功能的一小部分，而这些子集对于具有不同表示形式的Learner而言是不同的。因此，关键问题不是“可以代表吗？” 答案通常是微不足道的，但是“可以学习吗？” 尝试不同的Learner（并可能将他们组合）很值得。

Some representations are exponentially more compact than others for some functions. As a result, they may also require exponentially less data to learn those functions. Many learners work by forming linear combinations of simple basis functions. For example, support vector machines form combinations of kernels centered at some of the training examples (the support vectors). Representing parity of n bits in this way requires 2n basis functions. But using a representation with more layers (that is, more steps between input and output), parity can be encoded in a linear-size classifier. Finding methods to learn these deeper representations is one of the major research frontiers in machine learning.2

对于某些功能，某些表示形式比其他表示形式更紧凑。结果，他们可能还需要更少的数据来学习这些功能。许多Learner通过形成简单基函数的线性组合来工作。例如，支持向量机形成以一些训练示例（支持向量）为中心的内核组合。以这种方式表示n位的奇偶校验需要2 n个基函数。但是，使用具有更多层的表示（即输入和输出之间的更多步骤），可以将奇偶校验编码为线性大小的分类器。寻找学习这些更深层表示的方法是机器学习的主要研究领域之一。

12. Correlation Does Not Imply Causation / 相关并不暗示因果关系

The point that correlation does not imply causation is made so often that it is perhaps not worth belaboring. But, even though learners of the kind we have been discussing can only learn correlations, their results are often treated as representing causal relations. Isn’t this wrong? If so, then why do people do it?

关联并不意味着因果关系这一点经常被提出，以至于可能不值得进行研究。但是，即使我们一直在讨论的那种Learner只能学习相关性，其结果也经常被视为代表因果关系。这不是错吗？如果是这样，那人们为什么要这么做呢？

More often than not, the goal of learning predictive models is to use them as guides to action. If we find that beer and diapers are often bought together at the supermarket, then perhaps putting beer next to the diaper section will increase sales. (This is a famous example in the world of data mining.) But short of actually doing the experiment it is difficult to tell. Machine learning is usually applied to observational data, where the predictive variables are not under the control of the learner, as opposed to experimental data, where they are. Some learning algorithms can potentially extract causal information from observational data, but their applicability is rather restricted.19 On the other hand, correlation is a sign of a potential causal connection, and we can use it as a guide to further investigation (for example, trying to understand what the causal chain might be).

通常，学习预测模型的目的是将其用作行动指南。如果我们发现啤酒和尿布经常在超市一起购买，那么将啤酒放在尿布部分旁边可能会增加销量。（这是数据挖掘世界中的一个著名例子。）但是，如果没有实际进行实验，就很难说清楚。机器学习通常应用于观测数据，而预测数据则不受实验者的控制，而实验数据则受实验数据的控制。一些学习算法可以潜在地从观测数据中提取因果信息，但是其适用性受到很大限制。19 另一方面，相关性是潜在的因果关系的标志，我们可以将其用作进一步研究的指南（例如，尝试了解因果链可能是什么）。

Many researchers believe that causality is only a convenient fiction. For example, there is no notion of causality in physical laws. Whether or not causality really exists is a deep philosophical question with no definitive answer in sight, but there are two practical points for machine learners. First, whether or not we call them “causal,” we would like to predict the effects of our actions, not just correlations between observable variables. Second, if you can obtain experimental data (for example by randomly assigning visitors to different versions of a Web site), then by all means do so.14

许多研究人员认为因果关系只是一种方便的小说。例如，物理定律中没有因果关系的概念。因果关系是否真的存在是一个深层的哲学问题，没有明确的答案，但是对于机器Learner来说，有两个实用的观点。首先，无论我们是否称其为“因果关系”，我们都希望预测行为的影响，而不仅仅是预测变量之间的相关性。其次，如果您可以获得实验数据（例如，通过将访问者随机分配到网站的不同版本），则一定要这样做。14

0. Conclusion / 结论

Like any discipline, machine learning has a lot of “folk wisdom” that can be difficult to come by, but is crucial for success. This article summarized some of the most salient items. Of course, it is only a complement to the more conventional study of machine learning. Check out http://www.cs.washington.edu/homes/pedrod/class class for a complete online machine learning course that combines formal and informal aspects. There is also a treasure trove of machine learning lectures at http://www.videolectures.net. A good open source machine learning toolkit is Weka.24

像任何学科一样，机器学习具有很多“通俗知识”，这很难获得，但对成功至关重要。本文总结了一些最突出的项目。当然，它只是对传统机器学习的补充。请访问http://www.cs.washington.edu/homes/pedrod/class，以获取结合了正式和非正式方面的完整在线机器学习课程。在http://www.videolectures.net上还有一个机器学习讲座宝库。Weka是一个很好的开源机器学习工具包。24

Happy learning!

学习愉快！

---

1. error ↩︎

2. error ↩︎

3. error ↩︎

4. error ↩︎

5. ↩︎ ↩︎