梯度下降(一):批梯度下降、随机梯度下降、小批量梯度下降、动量梯度下降、Nesterov加速梯度下降法 Matlab 可视化实现
梯度下降 (一): 批梯度下降、随机梯度下降、小批量梯度下降、动量梯度下降、Nesterov加速梯度下降法
-
-
- 前言
- 梯度下降法(GD / Gradient Descent)
- 单变量线性回归模型(Univariate Linear Regression)
- 批梯度下降法(Batch GD / Batch Gradient Descent)
- 随机梯度下降法(SGD / Stochastic Gradient Descent)
- 小批量梯度下降(Mini Batch GD / Mini-batch Gradient Descent)
- 动量梯度下降(Momentum / Gradient Descent with Momentum)
- Nesterov加速梯度下降法(NAG / Nesterov Accelerated Gradient)
- 后语
-
前言
本文通过使用单变量线性回归模型讲解一些常见的梯度下降算法。为了更好的作对比,我们对参数设置了不同的学习率。
梯度下降法(GD / Gradient Descent)
梯度下降法(Gradient Descent)是一种常见的、用于寻找函数极小值的一阶迭代优化算法,又称为最速下降(Steepest Descent),它是求解无约束最优化问题的一种常用方法。以下是梯度下降的基本公式:
θ : = θ − ∂ J ( θ ) ∂ θ \theta := \theta - \frac{\partial J(\theta)}{\partial \theta} θ:=θ−∂θ∂J(θ)
其中 J ( θ ) J(\theta) J(θ) 是关于参数 θ \theta θ 的损失函数, η \eta η 是学习率(正标量),也称为梯度下降的步长。由上述公式可知,梯度下降的想法是使得参数 θ \theta θ 向着负梯度方向做更新迭代。
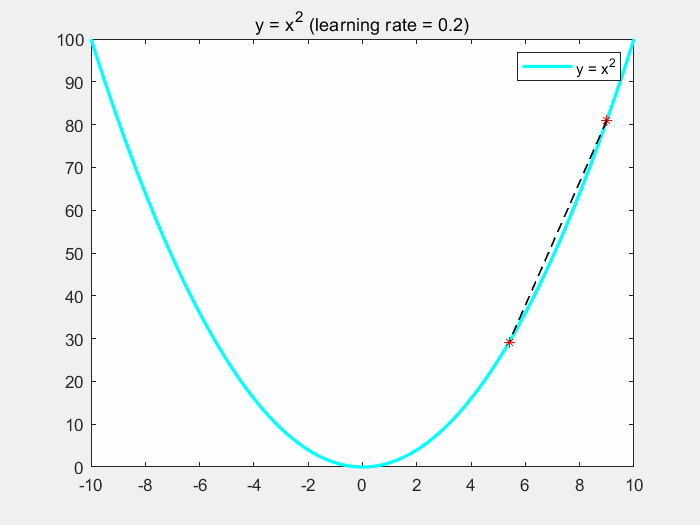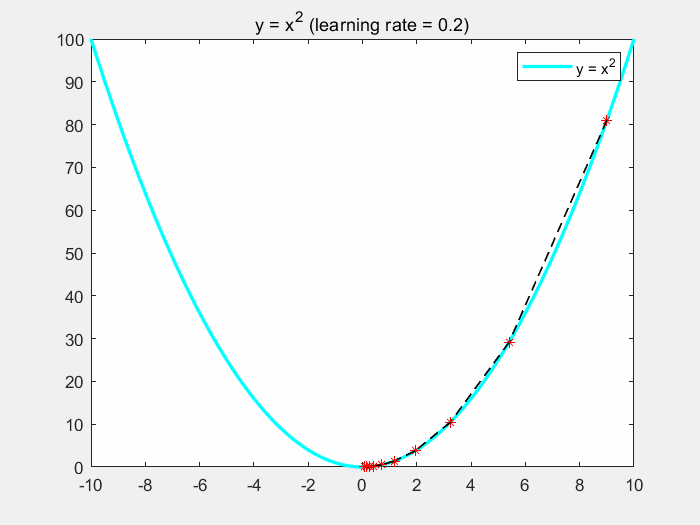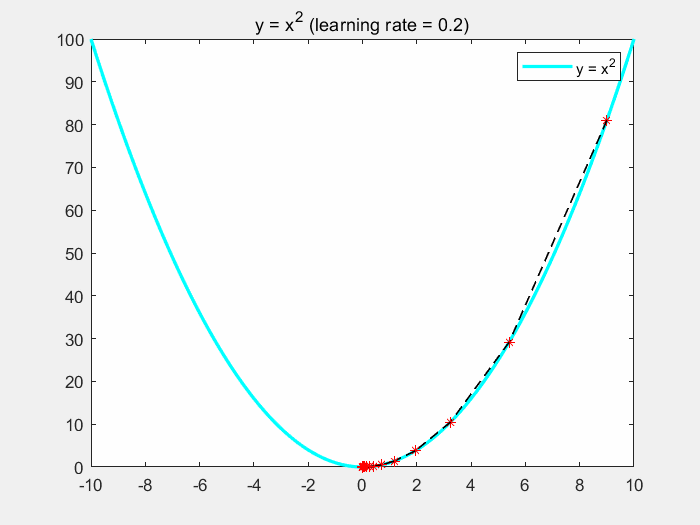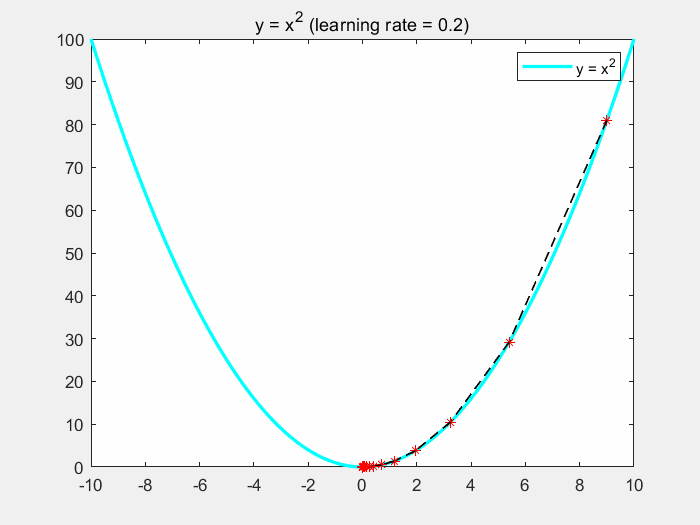
下面通过一个简单的例子来直观了解梯度下降的过程。假设 J ( θ ) J(\theta) J(θ) 为关于 θ \theta θ 的一元二次函数,即 J ( θ ) = θ 2 J(\theta) = \theta^2 J(θ)=θ2。假设初始值为 ( θ , J ( θ ) ) = ( 9 , 81 ) (\theta, J(\theta)) = (9,81) (θ,J(θ))=(9,81), η = 0.2 。 \eta = 0.2。 η=0.2。对于第一次迭代,求取梯度为: ∂ J ( θ ) ∂ θ = 2 θ = 18 \frac{\partial J(\theta)}{\partial \theta} = 2\theta = 18 ∂θ∂J(θ)=2θ=18,更新 θ : = θ − ∂ J ( θ ) ∂ θ = 9 − 0.2 ∗ 18 = 5.4 \theta := \theta - \frac{\partial J(\theta)}{\partial \theta} = 9 - 0.2*18 = 5.4 θ:=θ−∂θ∂J(θ)=9−0.2∗18=5.4。继续重复迭代步骤,最后函数将会趋于极值点 x = 0 x = 0 x=0。
如下图所示,我们可以发现,随着梯度的不断减小,函数收敛越来越慢:
下面是该程序的matlab代码:
% writen by: Weichen Gu, date: 4/18th/2020
clc; clf; clear;
xdata = linspace(-10,10,1000); % x range
f = @(xdata)(xdata.^2); % Quadratic function - loss function
ydata = f(xdata);
plot(xdata,ydata,'c','linewidth',2);
title('y = x^2 (learning rate = 0.2)');
hold on;
x = [9 f(9)]; % Initial point
slope = inf; % Slope
LRate = 0.2; % Learning rate
slopeThresh = 0.0001; % Slope threshold for iteration
plot(x(1),x(2),'r*');
while abs(slope) > slopeThresh
[tmp,slope] = gradientDescent(x(1),f,LRate);
x1 = [tmp f(tmp)];
line([x(1),x1(1)],[x(2),x1(2)],'color','k','linestyle','--','linewidth',1);
plot(x1(1),x1(2),'r*');
legend('y = x^2');
drawnow;
x = x1;
end
hold off
function [xOut,slope] = gradientDescent(xIn,f, eta)
syms x;
slope = double(subs(diff(f(x)),xIn));
xOut = xIn- eta*(slope);
end学习率决定了梯度下降的收敛速度,合适的学习率会使收敛速度得到一定的提高。我们应该避免过小或者过大的学习率:
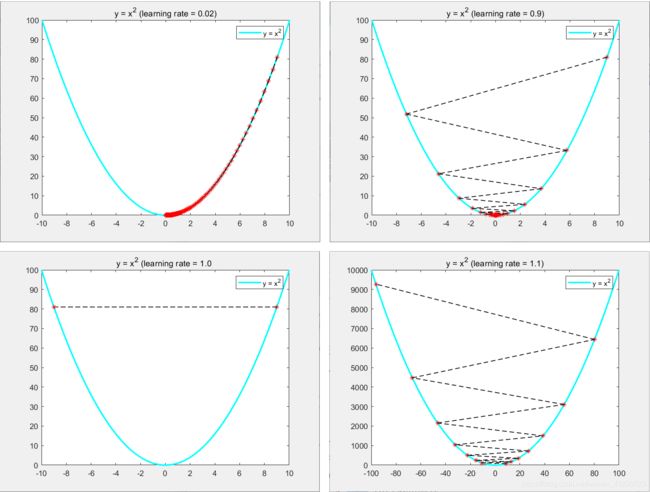
- 学习率过小会导致函数收敛速度非常慢,所需迭代次数多,难以收敛。
- 学习率过大会导致梯度下降过程中出现震荡、不收敛甚至发散的情况。
如下图所示:
对于学习率,一开始可以设置较大的步长,然后再慢慢减小步长来调整收敛速度,但是实际过程中,设置最优的学习率一般来说是比较困难的。
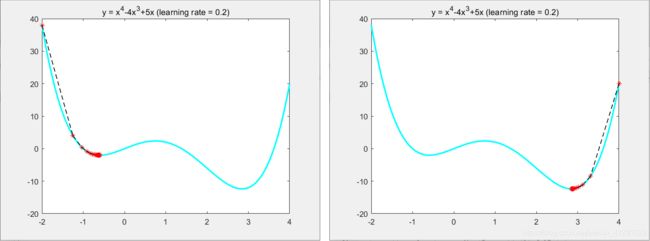
同时我们应该知道,梯度下降是一种寻找函数极小值的方法,如下图,不同的初始点可能会获得不同的极小值:
单变量线性回归模型(Univariate Linear Regression)
下面我们通过使用吴恩达老师课程中的单变量线性回归(Univariate Linear Regression)模型来讲解几种梯度下降策略。如下公式:
h θ ( x ) = θ 0 x + θ 1 h_{\theta}(x) = \theta_0 x+\theta_1 hθ(x)=θ0x+θ1
它是一种简单的线性拟合模型,并且目标函数为凸函数(根据一阶导二阶导性质),所以对于梯度下降求得的极小值就是损失函数的最优解。下列公式为单变量线性回归模型的损失函数/目标函数:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(\theta_0,\theta_1) = \frac{1}{2m}\sum_{i = 1}^m(h_{\theta}(x^i)-y^i)^2 J(θ0,θ1)=2m1i=1∑m(hθ(xi)−yi)2
其中 h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i))是通过回归模型预测的输出。 m m m为样本个数。
我们的目标是求出使得目标函数最小的参数值
( θ ^ 0 , θ ^ 1 ) = arg min θ 0 , θ 1 J ( θ 0 , θ 1 ) (\hat\theta_0,\hat\theta_1) = \argmin_{\theta_0,\theta_1}J(\theta_0,\theta_1) (θ^0,θ^1)=θ0,θ1argminJ(θ0,θ1)
对损失函数进行梯度求解,可得到:
∂ J ( θ 0 , θ 1 ) ∂ θ 0 = 1 m ∑ i = 1 m ( θ 0 + θ 1 x i − y i ) \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} = \frac{1}{m}\sum_{i = 1}^m(\theta_0+\theta_1x^i -y^i) ∂θ0∂J(θ0,θ1)=m1i=1∑m(θ0+θ1xi−yi) ∂ J ( θ 0 , θ 1 ) ∂ θ 1 = 1 m ∑ i = 1 m ( θ 0 + θ 1 x i − y i ) x i \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} = \frac{1}{m}\sum_{i = 1}^m(\theta_0+\theta_1x^i -y^i)x^i ∂θ1∂J(θ0,θ1)=m1i=1∑m(θ0+θ1xi−yi)xi
批梯度下降法(Batch GD / Batch Gradient Descent)
批梯度下降法根据整个数据集求取损失函数的梯度,来更新参数 θ \theta θ的值。公式如下:
θ : = θ − η ⋅ 1 m ∑ i = 1 m ∂ J ( θ , x i , y i ) ∂ θ \theta := \theta - \eta\cdot\frac{1}{m}\sum_{i=1}^m\frac{\partial J(\theta,x^i,y^i)}{\partial \theta} θ:=θ−η⋅m1i=1∑m∂θ∂J(θ,xi,yi)
优点:考虑到了全局数据,更新稳定,震荡小,每次更新都会朝着正确的方向。
缺点:如果数据集比较大,会造成大量时间和空间开销。
下图显示了通过批梯度下降进行拟合的结果。根据图像可看到,我们的线性回归模型逐渐拟合到了一个不错的结果。
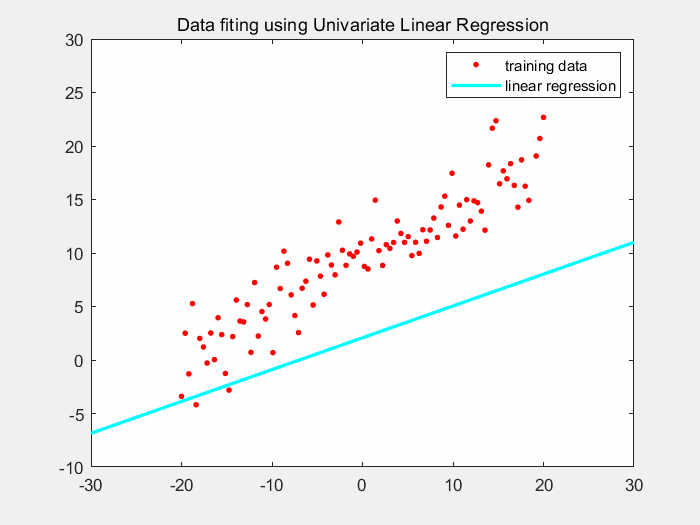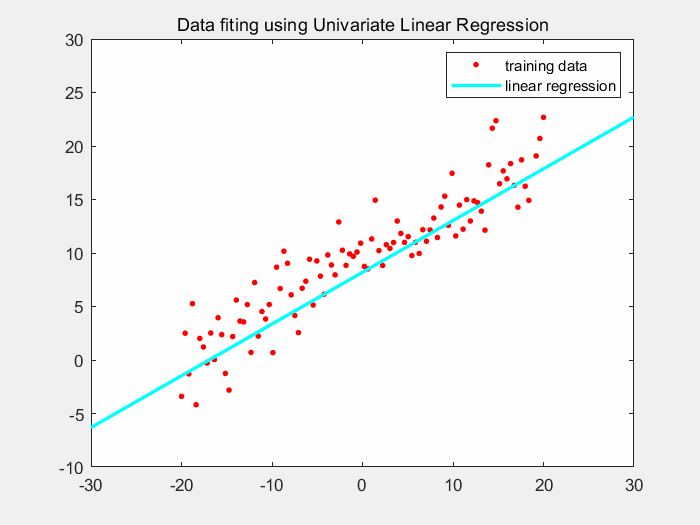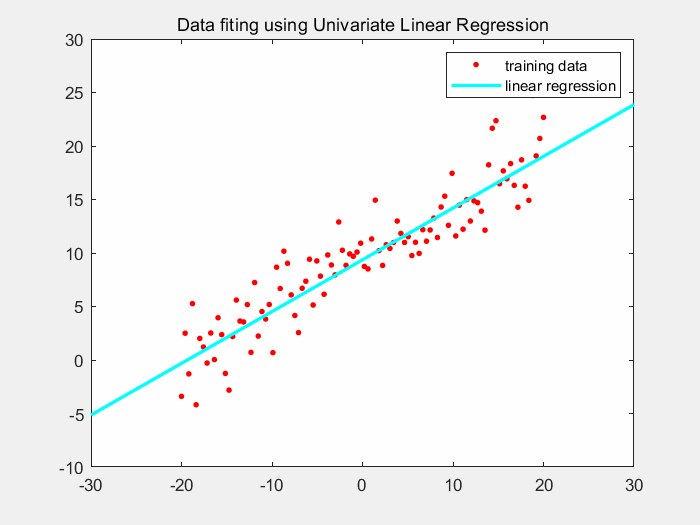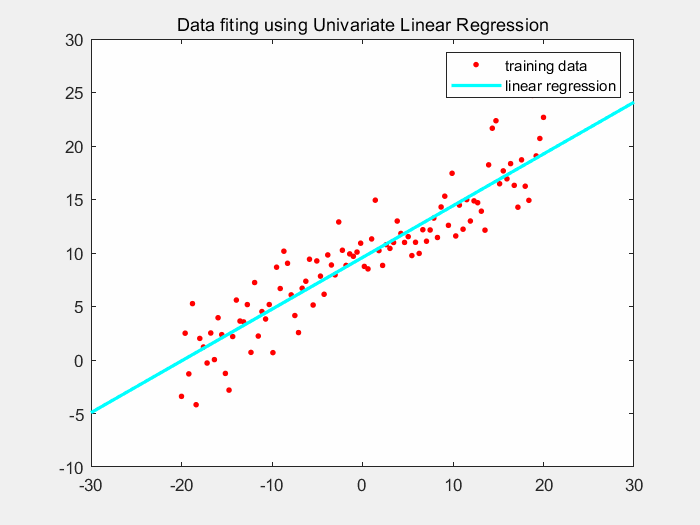
下面给出matlab的代码:
% Writen by weichen GU, data 4/19th/2020
clear, clf, clc;
data = linspace(-20,20,100); % x range
col = length(data); % Obtain the number of x
data = [data;0.5*data + wgn(1,100,1).*2+10]; % Generate dataset - y = 0.5 * x + wgn^2 + 10;
X = [ones(1, col); data(1,:)]'; % X ->[1;X];
plot(data(1,:),data(2,:),'r.','MarkerSize',10); % Plot data
title('Data fiting using Univariate Linear Regression');
axis([-30,30,-10,30])
hold on;
theta =[0;0]; % Initialize parameters
LRate = [0.1; 0.002]; % Learning rate
thresh = 0.5; % Threshold of loss for jumping iteration
iteration = 40; % The number of teration
lineX = linspace(-30,30,100);
[row, col] = size(data) % Obtain the size of dataset
lineMy = [lineX;theta(1)*lineX+theta(2)]; % Fitting line
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
for iter = 1 : iteration
delete(hLine) % set(hLine,'visible','off')
[thetaOut] = GD(X,data(2,:)',theta,LRate); % Gradient Descent algorithm
theta = thetaOut; % Update parameters(theta)
loss = getLoss(X,data(2,:)',col,theta); % Obtain the loss
lineMy(2,:) = theta(2)*lineX+theta(1); % Fitting line
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
drawnow()
if(loss < thresh)
break;
end
end
hold off
function [thetaOut] = GD(X,Y,theta,LRate)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize*(X'*(X*theta-Y)); % Obtain the gradient
thetaOut = theta -LRate.*dx; % gradient descent method
end
function [Z] = getLoss(X,Y, num,theta)
Z= 1/(2*num)*sum((X*theta-Y).^2);
end
我们希望可以直观的看到批梯度下降的过程,以便和后续的一些梯度下降算法作比较,于是我们将其三维可视化出来,画出其拟合图(1)、三维损失图(2)、等高线图(3)以及迭代损失图(4):
根据上图可以看到,批梯度下降收敛稳定,震荡小。
这里给出具体matlab实现代码:
% Writen by weichen GU, data 4/19th/2020
clear, clf, clc;
data = linspace(-20,20,100); % x range
col = length(data); % Obtain the number of x
data = [data;0.5*data + wgn(1,100,1)+10]; % Generate dataset - y = 0.5 * x + wgn^2 + 10;
X = [ones(1, col); data(1,:)]'; % X ->[1;X];
t1=-40:0.1:50;
t2=-4:0.1:4;
[meshX,meshY]=meshgrid(t1,t2);
meshZ = getTotalCost(X, data(2,:)', col, meshX,meshY);
theta =[-30;-4]; % Initialize parameters
LRate = [0.1; 0.002]; % Learning rate
thresh = 0.5; % Threshold of loss for jumping iteration
iteration = 50; % The number of teration
lineX = linspace(-30,30,100);
[row, col] = size(data) % Obtain the size of dataset
lineMy = [lineX;theta(1)*lineX+theta(2)]; % Fitting line
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
loss = getLoss(X,data(2,:)',col,theta); % Obtain current loss value
subplot(2,2,1);
plot(data(1,:),data(2,:),'r.','MarkerSize',10);
title('Data fiting using Univariate LR');
axis([-30,30,-10,30])
xlabel('x');
ylabel('y');
hold on;
% Draw 3d loss surfaces
subplot(2,2,2)
mesh(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('3D surfaces for loss')
hold on;
scatter3(theta(1),theta(2),loss,'r*');
% Draw loss contour figure
subplot(2,2,3)
contour(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('Contour figure for loss')
hold on;
plot(theta(1),theta(2),'r*')
% Draw loss with iteration
subplot(2,2,4)
hold on;
title('Loss when using Batch GD');
xlabel('iter');
ylabel('loss');
plot(0,loss,'b*');
set(gca,'XLim',[0 iteration]);
%set(gca,'YLim',[0 4000]);
hold on;
for iter = 1 : iteration
delete(hLine) % set(hLine,'visible','off')
[thetaOut] = GD(X,data(2,:)',theta,LRate); % Gradient Descent algorithm
subplot(2,2,3);
line([theta(1),thetaOut(1)],[theta(2),thetaOut(2)],'color','k')
theta = thetaOut;
loss = getLoss(X,data(2,:)',col,theta); % Obtain losw
lineMy(2,:) = theta(2)*lineX+theta(1); % Fitting line
subplot(2,2,1);
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
%legend('training data','linear regression');
subplot(2,2,2);
scatter3(theta(1),theta(2),loss,'r*');
subplot(2,2,3);
plot(theta(1),theta(2),'r*')
subplot(2,2,4)
plot(iter,loss,'b*');
drawnow();
if(loss < thresh)
break;
end
end
hold off
function [Z] = getTotalCost(X,Y, num,meshX,meshY);
[row,col] = size(meshX);
Z = zeros(row, col);
for i = 1 : row
theta = [meshX(i,:); meshY(i,:)];
Z(i,:) = 1/(2*num)*sum((X*theta-repmat(Y,1,col)).^2);
end
end
function [Z] = getLoss(X,Y, num,theta)
Z= 1/(2*num)*sum((X*theta-Y).^2);
end
function [thetaOut] = GD(X,Y,theta,eta)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*theta-Y)); % Obtain the gradient of Loss function
thetaOut = theta -eta.*dx; % Update parameters(theta)
end
随机梯度下降法(SGD / Stochastic Gradient Descent)
因为批梯度下降所需要的时间空间成本大,我们考虑随机抽取一个样本来获取梯度,更新参数 θ \theta θ。其公式如下:
θ : = θ − η ⋅ ∂ J ( θ , x i , y i ) ∂ θ \theta := \theta - \eta\cdot\frac{\partial J(\theta,x^i,y^i)}{\partial \theta} θ:=θ−η⋅∂θ∂J(θ,xi,yi)步骤如下:
- 随机打乱数据集。
- 对于每个样本点,依次迭代更新参数 θ \theta θ。
- 重复以上步骤直至损失足够小或到达迭代阈值。
优点:训练速度快,每次迭代只需要一个样本,相对于批梯度下降,总时间、空间开销小。
缺点:噪声大导致高方差。导致每次迭代并不一定朝着最优解收敛,震荡大。
下图直观显示了随机梯度下降的迭代过程:
下面给出随机梯度下降的matlab代码,因为它是小批量梯度下降的特殊情况(batchSize = 1),所以我将小批量梯度下降的代码放在本章节,并设置batchSize = 1。
% Writen by weichen GU, data 4/19th/2020
clear, clf, clc;
data = linspace(-20,20,100); % x range
col = length(data); % Obtain the number of x
data = [data;0.5*data + wgn(1,100,1)+10]; % Generate dataset - y = 0.5 * x + wgn^2 + 10;
X = [ones(1, col); data(1,:)]'; % X ->[1;X];
t1=-40:0.1:50;
t2=-4:0.1:4;
[meshX,meshY]=meshgrid(t1,t2);
meshZ = getTotalCost(X, data(2,:)', col, meshX,meshY);
theta =[-30;-4]; % Initialize parameters
LRate = [0.1; 0.002] % Learning rate
thresh = 0.5; % Threshold of loss for jumping iteration
iteration = 100; % The number of teration
lineX = linspace(-30,30,100);
[row, col] = size(data) % Obtain the size of dataset
lineMy = [lineX;theta(1)*lineX+theta(2)]; % Fitting line
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
loss = getLoss(X,data(2,:)',col,theta); % Obtain current loss value
subplot(2,2,1);
plot(data(1,:),data(2,:),'r.','MarkerSize',10);
title('Data fiting using Univariate LR');
axis([-30,30,-10,30])
xlabel('x');
ylabel('y');
hold on;
% Draw 3d loss surfaces
subplot(2,2,2)
mesh(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('3D surfaces for loss')
hold on;
scatter3(theta(1),theta(2),loss,'r*');
% Draw loss contour figure
subplot(2,2,3)
contour(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('Contour figure for loss')
hold on;
plot(theta(1),theta(2),'r*')
% Draw loss with iteration
subplot(2,2,4)
hold on;
title('Loss when using SGD');
xlabel('iter');
ylabel('loss');
plot(0,loss,'b*');
set(gca,'XLim',[0 iteration]);
hold on;
batchSize = 1;
for iter = 1 : iteration
delete(hLine) % set(hLine,'visible','off')
%[thetaOut] = GD(X,data(2,:)',theta,LRate); % Gradient Descent algorithm
[thetaOut] = MBGD(X,data(2,:)',theta,LRate,batchSize);
subplot(2,2,3);
line([theta(1),thetaOut(1)],[theta(2),thetaOut(2)],'color','k')
theta = thetaOut;
loss = getLoss(X,data(2,:)',col,theta); % Obtain losw
lineMy(2,:) = theta(2)*lineX+theta(1); % Fitting line
subplot(2,2,1);
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
%legend('training data','linear regression');
subplot(2,2,2);
scatter3(theta(1),theta(2),loss,'r*');
subplot(2,2,3);
plot(theta(1),theta(2),'r*')
subplot(2,2,4)
plot(iter,loss,'b*');
drawnow();
if(loss < thresh)
break;
end
end
hold off
function [Z] = getTotalCost(X,Y, num,meshX,meshY);
[row,col] = size(meshX);
Z = zeros(row, col);
for i = 1 : row
theta = [meshX(i,:); meshY(i,:)];
Z(i,:) = 1/(2*num)*sum((X*theta-repmat(Y,1,col)).^2);
end
end
function [Z] = getLoss(X,Y, num,theta)
Z= 1/(2*num)*sum((X*theta-Y).^2);
end
function [thetaOut] = GD(X,Y,theta,eta)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*theta-Y)); % Obtain the gradient of Loss function
thetaOut = theta -eta.*dx; % Update parameters(theta)
end
% @ Depscription:
% Mini-batch Gradient Descent (MBGD)
% Stochastic Gradient Descent(batchSize = 1) (SGD)
% @ param:
% X - [1 X_] X_ is actual X; Y - actual Y
% theta - theta for univariate linear regression y_pred = theta_0 + theta1*x
% eta - learning rate;
%
function [thetaOut] = MBGD(X,Y,theta, eta,batchSize)
dataSize = length(X); % obtain the number of data
k = fix(dataSize/batchSize); % obtain the number of batch which has absolutely same size: k = batchNum-1;
batchIdx = randperm(dataSize); % randomly sort for every epoch for achiving sample diversity
batchIdx1 = reshape(batchIdx(1:k*batchSize),k,batchSize); % batches which has absolutely same size
batchIdx2 = batchIdx(k*batchSize+1:end); % ramained batch
for i = 1 : k
thetaOut = GD(X(batchIdx1(i,:),:),Y(batchIdx1(i,:)),theta,eta);
end
if(~isempty(batchIdx2))
thetaOut = GD(X(batchIdx2,:),Y(batchIdx2),thetaOut,eta);
end
end
小批量梯度下降(Mini Batch GD / Mini-batch Gradient Descent)
随机梯度下降收敛速度快,但是波动较大,在最优解处出现波动很难判断其是否收敛到一个合理的值。而批梯度下降稳定但是时空开销很大,针对于这种情况,我们引入小批量梯度下降对二者进行折衷,在每轮迭代过程中使用n个样本来训练参数:
θ : = θ − η ⋅ 1 n ∑ i = 1 n ∂ J ( θ , x i , y i ) ∂ θ \theta := \theta - \eta\cdot\frac{1}{n}\sum_{i=1}^n\frac{\partial J(\theta,x^i,y^i)}{\partial \theta} θ:=θ−η⋅n1i=1∑n∂θ∂J(θ,xi,yi)步骤如下:
- 随机打乱数据集。
- 将数据集分为 m n \frac{m}{n} nm个集合,如果有余,将剩余样本单独作为一个集合。
- 依次对于这些集合做批梯度下降,更新参数 θ \theta θ。
- 重复上述步骤,直至损失足够小或达到迭代阈值。
下图显示了小批量梯度下降的迭代过程,其中batchSize = 32。我们可以看到,小批量折衷了批梯度下降和随机梯度下降的特点,做到了相对来说收敛快、较稳定的结果。
这里附上小批量梯度下降的相关代码:
% Writen by weichen GU, data 4/19th/2020
clear, clf, clc;
data = linspace(-20,20,100); % x range
col = length(data); % Obtain the number of x
data = [data;0.5*data + wgn(1,100,1)+10]; % Generate dataset - y = 0.5 * x + wgn^2 + 10;
X = [ones(1, col); data(1,:)]'; % X ->[1;X];
t1=-40:0.1:50;
t2=-4:0.1:4;
[meshX,meshY]=meshgrid(t1,t2);
meshZ = getTotalCost(X, data(2,:)', col, meshX,meshY);
theta =[-30;-4]; % Initialize parameters
LRate = [0.1; 0.002] % Learning rate
thresh = 0.5; % Threshold of loss for jumping iteration
iteration = 50; % The number of teration
lineX = linspace(-30,30,100);
[row, col] = size(data) % Obtain the size of dataset
lineMy = [lineX;theta(1)*lineX+theta(2)]; % Fitting line
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
loss = getLoss(X,data(2,:)',col,theta); % Obtain current loss value
subplot(2,2,1);
plot(data(1,:),data(2,:),'r.','MarkerSize',10);
title('Data fiting using Univariate LR');
axis([-30,30,-10,30])
xlabel('x');
ylabel('y');
hold on;
% Draw 3d loss surfaces
subplot(2,2,2)
mesh(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('3D surfaces for loss')
hold on;
scatter3(theta(1),theta(2),loss,'r*');
% Draw loss contour figure
subplot(2,2,3)
contour(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('Contour figure for loss')
hold on;
plot(theta(1),theta(2),'r*')
% Draw loss with iteration
subplot(2,2,4)
hold on;
title('Loss when using Mini-Batch GD');
xlabel('iter');
ylabel('loss');
plot(0,loss,'b*');
set(gca,'XLim',[0 iteration]);
%set(gca,'YLim',[0 4000]);
hold on;
batchSize = 32;
for iter = 1 : iteration
delete(hLine) % set(hLine,'visible','off')
%[thetaOut] = GD(X,data(2,:)',theta,LRate); % Gradient Descent algorithm
[thetaOut] = MBGD(X,data(2,:)',theta,LRate,batchSize);
subplot(2,2,3);
line([theta(1),thetaOut(1)],[theta(2),thetaOut(2)],'color','k')
theta = thetaOut;
loss = getLoss(X,data(2,:)',col,theta); % Obtain losw
lineMy(2,:) = theta(2)*lineX+theta(1); % Fitting line
subplot(2,2,1);
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
%legend('training data','linear regression');
subplot(2,2,2);
scatter3(theta(1),theta(2),loss,'r*');
subplot(2,2,3);
plot(theta(1),theta(2),'r*')
subplot(2,2,4)
plot(iter,loss,'b*');
drawnow();
if(loss < thresh)
break;
end
end
hold off
function [Z] = getTotalCost(X,Y, num,meshX,meshY);
[row,col] = size(meshX);
Z = zeros(row, col);
for i = 1 : row
theta = [meshX(i,:); meshY(i,:)];
Z(i,:) = 1/(2*num)*sum((X*theta-repmat(Y,1,col)).^2);
end
end
function [Z] = getLoss(X,Y, num,theta)
Z= 1/(2*num)*sum((X*theta-Y).^2);
end
function [thetaOut] = GD(X,Y,theta,eta)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*theta-Y)); % Obtain the gradient of Loss function
thetaOut = theta -eta.*dx; % Update parameters(theta)
end
% @ Depscription:
% Mini-batch Gradient Descent (MBGD)
% Stochastic Gradient Descent(batchSize = 1) (SGD)
% @ param:
% X - [1 X_] X_ is actual X; Y - actual Y
% theta - theta for univariate linear regression y_pred = theta_0 + theta1*x
% eta - learning rate;
%
function [thetaOut] = MBGD(X,Y,theta, eta,batchSize)
dataSize = length(X); % obtain the number of data
k = fix(dataSize/batchSize); % obtain the number of batch which has absolutely same size: k = batchNum-1;
batchIdx = randperm(dataSize); % randomly sort for every epoch for achiving sample diversity
batchIdx1 = reshape(batchIdx(1:k*batchSize),k,batchSize); % batches which has absolutely same size
batchIdx2 = batchIdx(k*batchSize+1:end); % ramained batch
for i = 1 : k
thetaOut = GD(X(batchIdx1(i,:),:),Y(batchIdx1(i,:)),theta,eta);
end
if(~isempty(batchIdx2))
thetaOut = GD(X(batchIdx2,:),Y(batchIdx2),thetaOut,eta);
end
end
动量梯度下降(Momentum / Gradient Descent with Momentum)
动量梯度下降通过指数加权平均(Exponentially weighted moving averages)策略,使用之前梯度信息修正当前梯度,来加速参数学习。这里我们令梯度项
1 m ∑ i = 1 m ∂ J ( θ , x i , y i ) ∂ θ = ∇ θ J ( θ ) \frac{1}{m}\sum_{i=1}^m\frac{\partial J(\theta,x^i,y^i)}{\partial \theta} = \nabla_\theta J(\theta) m1i=1∑m∂θ∂J(θ,xi,yi)=∇θJ(θ)则梯度下降可以简化表示为
θ : = θ − η ⋅ ∇ θ J ( θ ) \theta := \theta - \eta\cdot\nabla_\theta J(\theta) θ:=θ−η⋅∇θJ(θ)
对于动量梯度下降,初始化动量项 m = 0 m = 0 m=0,更新迭代公式如下
m : = γ ⋅ m + η ⋅ ∇ θ J ( θ ) m := \gamma\cdot m + \eta\cdot\nabla_\theta J(\theta) m:=γ⋅m+η⋅∇θJ(θ) θ : = θ − m \theta :=\theta - m θ:=θ−m
其中 m m m为动量梯度下降的动量项,且初始化为0; γ \gamma γ是关于动量项的超参数一般取小于等于0.9。我们可以发现,越是远离当前点的梯度信息,对于当前梯度的贡献越小。
优点:通过过去梯度信息来优化下降速度,如果当前梯度与之前梯度方向一致时候,收敛速度得到加强,反之则减弱。换句话说,加快收敛同时减小震荡,分别对应图中 θ 0 \theta_0 θ0 与 θ 1 \theta_1 θ1 方向。
缺点:可能在下坡过程中累计动量太大,冲过极小值点。
下图直观显示动量梯度下降迭代过程。
这里附上动量梯度下降的相关代码:
% Writen by weichen GU, data 4/19th/2020
clear, clf, clc;
data = linspace(-20,20,100); % x range
col = length(data); % Obtain the number of x
data = [data;0.5*data + wgn(1,100,1)+10]; % Generate dataset - y = 0.5 * x + wgn^2 + 10;
X = [ones(1, col); data(1,:)]'; % X ->[1;X];
t1=-40:0.1:50;
t2=-4:0.1:4;
[meshX,meshY]=meshgrid(t1,t2);
meshZ = getTotalCost(X, data(2,:)', col, meshX,meshY);
theta =[-30;-4]; % Initialize parameters
LRate = [0.1; 0.002] % Learning rate
thresh = 0.5; % Threshold of loss for jumping iteration
iteration = 50; % The number of teration
lineX = linspace(-30,30,100);
[row, col] = size(data) % Obtain the size of dataset
lineMy = [lineX;theta(1)*lineX+theta(2)]; % Fitting line
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
loss = getLoss(X,data(2,:)',col,theta); % Obtain current loss value
subplot(2,2,1);
plot(data(1,:),data(2,:),'r.','MarkerSize',10);
title('Data fiting using Univariate LR');
axis([-30,30,-10,30])
xlabel('x');
ylabel('y');
hold on;
% Draw 3d loss surfaces
subplot(2,2,2)
mesh(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('3D surfaces for loss')
hold on;
scatter3(theta(1),theta(2),loss,'r*');
% Draw loss contour figure
subplot(2,2,3)
contour(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('Contour figure for loss')
hold on;
plot(theta(1),theta(2),'r*')
% Draw loss with iteration
subplot(2,2,4)
hold on;
title('Loss when using Momentum GD');
xlabel('iter');
ylabel('loss');
plot(0,loss,'b*');
set(gca,'XLim',[0 iteration]);
hold on;
batchSize = 32;
grad = 0; gamma = 0.5;
for iter = 1 : iteration
delete(hLine) % set(hLine,'visible','off')
%[thetaOut] = GD(X,data(2,:)',theta,LRate); % Gradient Descent algorithm
%[thetaOut] = MBGD(X,data(2,:)',theta,LRate,20);
[thetaOut,grad] = MBGDM(X,data(2,:)',theta,LRate,batchSize,grad,gamma);
subplot(2,2,3);
line([theta(1),thetaOut(1)],[theta(2),thetaOut(2)],'color','k')
theta = thetaOut;
loss = getLoss(X,data(2,:)',col,theta); % Obtain losw
lineMy(2,:) = theta(2)*lineX+theta(1); % Fitting line
subplot(2,2,1);
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
%legend('training data','linear regression');
subplot(2,2,2);
scatter3(theta(1),theta(2),loss,'r*');
subplot(2,2,3);
plot(theta(1),theta(2),'r*')
subplot(2,2,4)
plot(iter,loss,'b*');
drawnow();
if(loss < thresh)
break;
end
end
hold off
function [Z] = getTotalCost(X,Y, num,meshX,meshY);
[row,col] = size(meshX);
Z = zeros(row, col);
for i = 1 : row
theta = [meshX(i,:); meshY(i,:)];
Z(i,:) = 1/(2*num)*sum((X*theta-repmat(Y,1,col)).^2);
end
end
function [Z] = getLoss(X,Y, num,theta)
Z= 1/(2*num)*sum((X*theta-Y).^2);
end
function [thetaOut] = GD(X,Y,theta,eta)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*theta-Y)); % Obtain the gradient of Loss function
thetaOut = theta -eta.*dx; % Update parameters(theta)
end
% Gradient Descent with Momentum
function [thetaOut, momentum] = GDM(X,Y,theta,eta,momentum,gamma)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*theta-Y)); % Obtain the gradient of Loss function
momentum = gamma*momentum +eta.*dx; % Obtain the momentum of gradient
thetaOut = theta - momentum; % Update parameters(theta)
end
% @ Depscription:
% Mini-batch Gradient Descent (MBGD)
% Stochastic Gradient Descent(batchSize = 1) (SGD)
% @ param:
% X - [1 X_] X_ is actual X; Y - actual Y
% theta - theta for univariate linear regression y_pred = theta_0 + theta1*x
% eta - learning rate;
%
function [thetaOut] = MBGD(X,Y,theta, eta,batchSize)
dataSize = length(X); % obtain the number of data
k = fix(dataSize/batchSize); % obtain the number of batch which has absolutely same size: k = batchNum-1;
batchIdx = randperm(dataSize); % randomly sort for every epoch for achiving sample diversity
batchIdx1 = reshape(batchIdx(1:k*batchSize),k,batchSize); % batches which has absolutely same size
batchIdx2 = batchIdx(k*batchSize+1:end); % ramained batch
for i = 1 : k
thetaOut = GD(X(batchIdx1(i,:),:),Y(batchIdx1(i,:)),theta,eta);
end
if(~isempty(batchIdx2))
thetaOut = GD(X(batchIdx2,:),Y(batchIdx2),thetaOut,eta);
end
end
function [thetaOut,grad] = MBGDM(X,Y,theta, eta,batchSize,grad,gamma)
dataSize = length(X); % obtain the number of data
k = fix(dataSize/batchSize); % obtain the number of batch which has absolutely same size: k = batchNum-1;
batchIdx = randperm(dataSize); % randomly sort for every epoch for achiving sample diversity
batchIdx1 = reshape(batchIdx(1:k*batchSize),k,batchSize); % batches which has absolutely same size
batchIdx2 = batchIdx(k*batchSize+1:end); % ramained batch
for i = 1 : k
[thetaOut,grad] = GDM(X(batchIdx1(i,:),:),Y(batchIdx1(i,:)),theta,eta,grad,gamma);
end
if(~isempty(batchIdx2))
[thetaOut,grad] = GDM(X(batchIdx2,:),Y(batchIdx2),thetaOut,eta,grad,gamma);
end
end
Nesterov加速梯度下降法(NAG / Nesterov Accelerated Gradient)
Nesterov加速梯度下降相比于动量梯度下降的区别是,通过使用未来梯度来更新动量。即将下一次的预测梯度 ∇ θ J ( θ − η ⋅ m ) \nabla_\theta J(\theta-\eta\cdot m) ∇θJ(θ−η⋅m)考虑进来。其更新公式如下:
m : = γ ⋅ m + η ⋅ ∇ θ J ( θ − γ ⋅ m ) m :=\gamma\cdot m+\eta\cdot\nabla_\theta J(\theta-\gamma\cdot m) m:=γ⋅m+η⋅∇θJ(θ−γ⋅m) θ : = θ − m \theta := \theta - m θ:=θ−m
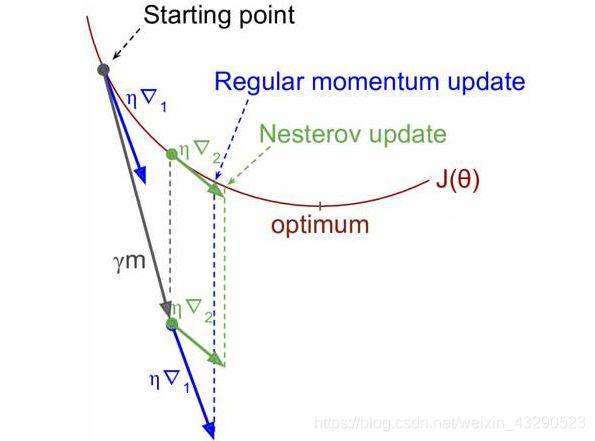
对于公式理解如下图所示,
- 对于起始点应用动量梯度下降,首先求得在该点处的带权梯度 η ⋅ ∇ 1 \eta\cdot\nabla_1 η⋅∇1,通过与之前动量 γ ⋅ m \gamma\cdot m γ⋅m矢量加权,求得下一次的 θ \theta θ位置。
- 对于起始点应用Nesterov加速梯度下降,首先通过先前动量求得 θ \theta θ的预测位置,再加上预测位置的带权梯度 γ ⋅ m \gamma\cdot m γ⋅m。
- 相对于动量梯度下降法,因为NAG考虑到了未来预测梯度,收敛速度更快(如上图)。
- 当更新幅度很大时,NAG可以抑制震荡。例如起始点在最优点的左侧
←, γ m \gamma m γm对应的值在最优点的右侧→,对于动量梯度而言,叠加 η ∇ 1 \eta\nabla_1 η∇1使得迭代后的点更加远离最优点→→。而NAG首先跳到 γ m \gamma m γm对应的值→,计算梯度为正,再叠加反方向的 η ∇ 2 \eta\nabla_2 η∇2←,从而达到抑制震荡的目的。
下图直观显示了Nesterov加速梯度下降的迭代过程:
下面是Nesterov加速梯度下降的相关代码:
% Writen by weichen GU, data 4/19th/2020
clear, clf, clc;
data = linspace(-20,20,100); % x range
col = length(data); % Obtain the number of x
data = [data;0.5*data + wgn(1,100,1)+10]; % Generate dataset - y = 0.5 * x + wgn^2 + 10;
X = [ones(1, col); data(1,:)]'; % X ->[1;X];
t1=-40:0.1:50;
t2=-4:0.1:4;
[meshX,meshY]=meshgrid(t1,t2);
meshZ = getTotalCost(X, data(2,:)', col, meshX,meshY);
theta =[-30;-4]; % Initialize parameters
LRate = [0.1; 0.002] % Learning rate
thresh = 0.5; % Threshold of loss for jumping iteration
iteration = 50; % The number of teration
lineX = linspace(-30,30,100);
[row, col] = size(data) % Obtain the size of dataset
lineMy = [lineX;theta(1)*lineX+theta(2)]; % Fitting line
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
loss = getLoss(X,data(2,:)',col,theta); % Obtain current loss value
subplot(2,2,1);
plot(data(1,:),data(2,:),'r.','MarkerSize',10);
title('Data fiting using Univariate LR');
axis([-30,30,-10,30])
xlabel('x');
ylabel('y');
hold on;
% Draw 3d loss surfaces
subplot(2,2,2)
mesh(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('3D surfaces for loss')
hold on;
scatter3(theta(1),theta(2),loss,'r*');
% Draw loss contour figure
subplot(2,2,3)
contour(meshX,meshY,meshZ)
xlabel('θ_0');
ylabel('θ_1');
title('Contour figure for loss')
hold on;
plot(theta(1),theta(2),'r*')
% Draw loss with iteration
subplot(2,2,4)
hold on;
title('Loss when using NAG');
xlabel('iter');
ylabel('loss');
plot(0,loss,'b*');
set(gca,'XLim',[0 iteration]);
hold on;
batchSize = 32;
grad = 0; gamma = 0.5;
for iter = 1 : iteration
delete(hLine) % set(hLine,'visible','off')
%[thetaOut] = GD(X,data(2,:)',theta,LRate); % Gradient Descent algorithm
%[thetaOut] = MBGD(X,data(2,:)',theta,LRate,20);
[thetaOut,grad] = MBGDM(X,data(2,:)',theta,LRate,batchSize,grad,gamma);
subplot(2,2,3);
line([theta(1),thetaOut(1)],[theta(2),thetaOut(2)],'color','k')
theta = thetaOut;
loss = getLoss(X,data(2,:)',col,theta); % Obtain losw
lineMy(2,:) = theta(2)*lineX+theta(1); % Fitting line
subplot(2,2,1);
hLine = plot(lineMy(1,:),lineMy(2,:),'c','linewidth',2); % draw fitting line
%legend('training data','linear regression');
subplot(2,2,2);
scatter3(theta(1),theta(2),loss,'r*');
subplot(2,2,3);
plot(theta(1),theta(2),'r*')
subplot(2,2,4)
plot(iter,loss,'b*');
drawnow();
if(loss < thresh)
break;
end
end
hold off
function [Z] = getTotalCost(X,Y, num,meshX,meshY);
[row,col] = size(meshX);
Z = zeros(row, col);
for i = 1 : row
theta = [meshX(i,:); meshY(i,:)];
Z(i,:) = 1/(2*num)*sum((X*theta-repmat(Y,1,col)).^2);
end
end
function [Z] = getLoss(X,Y, num,theta)
Z= 1/(2*num)*sum((X*theta-Y).^2);
end
function [thetaOut] = GD(X,Y,theta,eta)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*theta-Y)); % Obtain the gradient of Loss function
thetaOut = theta -eta.*dx; % Update parameters(theta)
end
% Gradient Descent with Momentum
function [thetaOut, momentum] = GDM(X,Y,theta,eta,momentum,gamma)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*theta-Y)); % Obtain the gradient of Loss function
momentum = gamma*momentum +eta.*dx; % Obtain the momentum of gradient
thetaOut = theta - momentum; % Update parameters(theta)
end
% @ Depscription:
% Mini-batch Gradient Descent (MBGD)
% Stochastic Gradient Descent(batchSize = 1) (SGD)
% @ param:
% X - [1 X_] X_ is actual X; Y - actual Y
% theta - theta for univariate linear regression y_pred = theta_0 + theta1*x
% eta - learning rate;
%
function [thetaOut] = MBGD(X,Y,theta, eta,batchSize)
dataSize = length(X); % obtain the number of data
k = fix(dataSize/batchSize); % obtain the number of batch which has absolutely same size: k = batchNum-1;
batchIdx = randperm(dataSize); % randomly sort for every epoch for achiving sample diversity
batchIdx1 = reshape(batchIdx(1:k*batchSize),k,batchSize); % batches which has absolutely same size
batchIdx2 = batchIdx(k*batchSize+1:end); % ramained batch
for i = 1 : k
thetaOut = GD(X(batchIdx1(i,:),:),Y(batchIdx1(i,:)),theta,eta);
end
if(~isempty(batchIdx2))
thetaOut = GD(X(batchIdx2,:),Y(batchIdx2),thetaOut,eta);
end
end
% Nesterov Accelerated Gradient (NAG)
function [thetaOut, momentum] = NAG(X,Y,theta,eta,momentum,gamma)
dataSize = length(X); % Obtain the number of data
dx = 1/dataSize.*(X'*(X*(theta- gamma*momentum)-Y)); % Obtain the gradient of Loss function
momentum = gamma*momentum +eta.*dx; % Obtain the momentum of gradient
thetaOut = theta - momentum; % Update parameters(theta)
end
function [thetaOut,grad] = MBGDM(X,Y,theta, eta,batchSize,grad,gamma)
dataSize = length(X); % obtain the number of data
k = fix(dataSize/batchSize); % obtain the number of batch which has absolutely same size: k = batchNum-1;
batchIdx = randperm(dataSize); % randomly sort for every epoch for achiving sample diversity
batchIdx1 = reshape(batchIdx(1:k*batchSize),k,batchSize); % batches which has absolutely same size
batchIdx2 = batchIdx(k*batchSize+1:end); % ramained batch
for i = 1 : k
%[thetaOut,grad] = GDM(X(batchIdx1(i,:),:),Y(batchIdx1(i,:)),theta,eta,grad,gamma);
[thetaOut,grad] = NAG(X(batchIdx1(i,:),:),Y(batchIdx1(i,:)),theta,eta,grad,gamma);
end
if(~isempty(batchIdx2))
%[thetaOut,grad] = GDM(X(batchIdx2,:),Y(batchIdx2),thetaOut,eta,grad,gamma);
[thetaOut,grad] = NAG(X(batchIdx2,:),Y(batchIdx2),thetaOut,eta,grad,gamma);
end
end
我们将 θ 1 \theta_1 θ1对应的学习率 η \eta η升高到0.005后,得到以下另一组数据方便对比。η=[0.1,0.005]
批梯度下降和随机梯度下降的迭代过程:
小批量梯度下降和动量梯度下降的迭代过程:
Nesterov加速梯度下降的迭代过程:
后语
下一篇我们将介绍几种常见的学习率自适应梯度下降算法:AdaGrad、RMSProp、AdaDelta、Adam和Nadam。