Linear Regression 线性回归
Linear Regression 线性回归
- 问题描述
- 构建模型
- 损失函数(Loss Function)
- 梯度下降(Gradient Descent)
- Learning Rate的选择
- 求取损失函数最小值
- 正则项
- 总结
- 代码实现
-
- 一次模型
- 二次模型
- 二次模型 Adamgrad
- 五次模型
- 五次模型 (With Regularization)
问题描述
房价预测:想要对一套房子进行估价,我们可以先在网上搜集已有的不同房屋面积对应的不同价格。可以假设这样一个线性模型,用我们已知的价格x乘以一个常数ω,再加上一个常数,从而得到一个预测的值y ̂ ,y ̂ = ω ∙ x + b,通过这个模型,已知房屋的面积,希望它能够帮我们预测出房屋的面积。将房屋的面积映射到模型中去,从而得出房屋对应的价格。
当然,决定一个房屋价格的因素不仅仅只有面积,比如说还有所处楼层以及距离市中心的距离等因素。我们称这些因素为Feature,也就是房屋的特征,而把价格称之为Label。
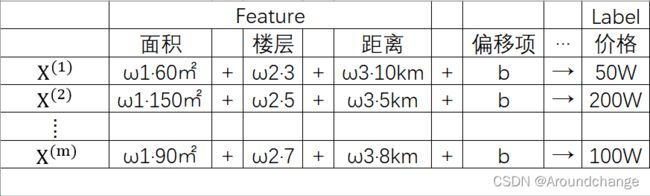
如上表所示,我们有m个房屋,每个房屋都有对应的特征,面积、楼层、距离等,以及它们各自的价格。我们还是希望有一个线性的模型能解决这个问题,我们将面积这个Feature乘以一个常数ω1,楼层这个Feature乘以一个常数ω2,距离这个Feature也乘以一个常数ω3。相乘之后我们把它们加在一起,然后再加上一个常数b,称之为偏移项,我们希望相加的结果能得到一个对应的价格。同理,每一个样本都是这样。
构建模型
将问题进行一般化描述:数据集为X,里面有1到m个样本,每个样本都有1到n个Feature。每个样本都有其对应的Label,为1到m个Y,如下表所示:

线性模型表示为:ω1 ∙ x1 + ω2 ∙ x2 + …… + ωn ∙ xn + b,我们将相加的结果赋值给y ̂,即:y ̂ = ω1 ∙ x1 + ω2 ∙ x2 + …… + ωn ∙ xn + b,也就是模型的预测值,紧凑地表示为:

模型构建好后,我们来进行求解。可以看出,x为训练集样本中的每一个数据,ω与b为模型的参数。
损失函数(Loss Function)
我们的模型为:y ̂ = ω1 ∙ x1 + ω2 ∙ x2 + …… + ωn ∙ xn + b,通过这个模型对训练集中的每一个数据进行预测,把1到m个样本中的1到n个Feature拿出来分别代入模型中,这样我们就得到了每一个样本基于模型的预测值,如下表所示:

得到这些值以后,我们将实际的Label与我们模型的预测值进行相减,也就是y(1) - y ̂ (1),y(2) - y ̂ (2),…,y(m) - y ̂ (m)。减完之后我们将它们加起来,(y(1) - y ̂ (1))+(y(2) - y ̂ (2))+…+(y(m) - y ̂ (m))。但是这样会存在一个问题:相减的值正负不确定,直接将相减的值再相加可能会出现正负抵消的情况,于是我们将每一项相减的值平方后再相加,这样的结果我们称之为损失(Loss),最终的损失函数为:

既然为损失函数,那么我们肯定希望它的值最小,也就是模型的预测值与它的实际值很接近,这就需要用到梯度下降算法。
梯度下降(Gradient Descent)
梯度下降是一种求取函数最小值的方法,我们需要找到一组值使得损失函数的值最小。也就是当(ω1*,ω2*,…,ωn*,b)带入L(ω1,ω2,…,ωn,b)有min(L(ω1,ω2,…,ωn,b))。

图中横坐标的参数为ω,纵坐标函数为L(ω),我们希望找到一点ω*,使得函数值最小,对应图中函数的最小值点,也就是min(L(ω))。我们可以先初始化一个值ω0,我们在ω0所对应的点处,图中的黑色点,求它的导数值。可以看出这一点的导数值大于0,同时ω0在ω* 的右边,我们希望ω0可以往左走一点,从而离ω* 的距离更近一点。我们可以用ω0的值减去η乘以该点的导数值,通常η也为正值,这样我们可以得到ω1,离ω* 更近一点。我们再在ω1所对应的这一点处求导数值,然后用ω1的值减去η乘以该点的导数值,从而得到ω2,离ω* 再近了一点。如此往复,到最后的时候我们就可以到达ω* 这一点,其中η在梯度下降里指的是学习率(Learning Rate),其作用为决定每一次改变ω0的多少,也即是每一次ω0向ω* 移动距离的大小。同理,ω0的初始位置也可以在ω* 的左侧,这时其对应的导数值为负,ω0的值减去η乘以该点的导数值便是整数,也即是向右移动,每移动一次就会离ω* 更近一点,直至到达ω* 这一点。

Learning Rate的选择

如果η的值很大,就会出现上图中Big learning rate的情况,而η的很小时,就会出现Small learning rate的情况。可以看出,η的值太大或太小都不适合,这时需要我们找到一个合适的η,使得梯度下降算法得到一个最好的效果。
求取损失函数最小值
对于损失函数,我们能进一步写得紧凑一些,即相应部分可以写成向量点乘的形式,如下图所示:

对于梯度下降算法来说,最重要的就是求每一个参数的偏导数,求解过程如下:

这样我们就得到了ω1的偏导,ω2的偏导,一直到ωn的偏导,还有b的偏导,有了这些偏导之后,我们就可以对我们的参数进行更新。我们的参数ω里有ω1,ω2,…,ωn,还有b。首先对它们进行初始化,初始化后可以更新参数。我们可以先初始化ω1的值,然后再减去学习率η乘以ω1的偏导数值,这就完成了对ω1的更新。以此类推,我们可以对ω2进行更新,用ω2的初始值减去学习率η乘以ω2的偏导数值,得到了一个新的ω2的值。同理,一直到ωn。对于b而言,也有b的初始值减去学习率η乘以b的偏导数值,得到了一个新的b的值。这样一来,我们就完成了第一次对所有参数的更新。我们可以进行很多次更新,直到找到了我们的最优解,也就是ω1更新到了它的最优解ω1*,ω2更新到了它的最优解ω12,一直到ωn更新到了它的最优解ωn*,b更新到了它的最优解b*。最优解可以让我们损失函数的值达到最小,也即是我们模型预测的值是最准确的。更新过程如下:

正则项
我们的损失函数为:

当ω这个向量太大时,会出现过拟合的情况,从而导致我们的模型很陡峭。求损失函数时我们希望L(ω1,ω2,…,ωn,b)最小,所以我们也希望ω最小,于是我们新的损失函数可以写成:

同理,ω1,ω2,…,ωn分别平方是为了避免正负抵消。损失函数中,加号前面是我们的模型,后面则是为了防止过拟合。λ的值可以调节我们关注过拟合的程度。当我们很关注过拟合时,λ的值则可以大一些,当我们不那么关注过拟合时,λ的值便可以相应变小。得到新的损失函数后,我们同样需要对其最小化,再次求偏导数:

损失函数中的λ也可为1/2λ,这样我们就能在求导的过程中将2抵消。为了避免出现ω正负抵消的情况,除了平方外,我们还可以将ω1,ω2,…,ωn分别加上绝对值。
总结
梯度下降算法分类
梯度下降算法可以根据计算梯度时使用训练集数据的数量分为以下三种:
- Batch Gradient Descent
- Stochastic Gradient Descent
- Mini-Batch Gradient Descent
当我们把训练集中所有的数据都用到的时候,我们采用的则是Batch Gradient Descent。而Stochastic Gradient Descent为随机梯度下降,每次只拿出一个数据来作为它的损失函数,针对这一个样本对其求偏导,再用该偏导值对参数进行更新,而Mini-Batch Gradient Descent则是取其中的一部分数据。
以上便是Linear Regression的理论部分
代码实现
- 数据集
import matplotlib.pyplot as plt
# 数据集
x = [12.3, 14.3, 14.5, 14.8, 16.1, 16.8, 16.5, 15.3, 17.0, 17.8, 18.7, 20.2, 22.3, 19.3, 15.5, 16.7, 17.2, 18.3, 19.2, 17.3, 19.5, 19.7, 21.2, 23.04, 23.8, 24.6, 25.2, 25.7, 25.9, 26.3]
y = [11.8, 12.7, 13.0, 11.8, 14.3, 15.3, 13.5, 13.8, 14.0, 14.9, 15.7, 18.8, 20.1, 15.0, 14.5, 14.9, 14.8, 16.4, 17.0, 14.8, 15.6, 16.4, 19.0, 19.8, 20.0, 20.3, 21.9, 22.1, 22.4, 22.6]
# print(len(x))
# 绘制数据集
plt.scatter(x, y)
plt.title('Dataset Samples')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
一次模型
import numpy as np
import matplotlib.pyplot as plt
# 数据集
x = [12.3, 14.3, 14.5, 14.8, 16.1, 16.8, 16.5, 15.3, 17.0, 17.8, 18.7, 20.2, 22.3, 19.3, 15.5, 16.7, 17.2, 18.3, 19.2, 17.3, 19.5, 19.7, 21.2, 23.04, 23.8, 24.6, 25.2, 25.7, 25.9, 26.3]
y = [11.8, 12.7, 13.0, 11.8, 14.3, 15.3, 13.5, 13.8, 14.0, 14.9, 15.7, 18.8, 20.1, 15.0, 14.5, 14.9, 14.8, 16.4, 17.0, 14.8, 15.6, 16.4, 19.0, 19.8, 20.0, 20.3, 21.9, 22.1, 22.4, 22.6]
# print(len(x))
# 分隔训练集和测试集
x_train = x[0: 20]
y_train = y[0: 20]
n_train = len(x_train)
x_test = x[20:]
y_test = y[20:]
n_test = len(x_test)
# Fit model y = w * x + b
# 初始值
# parameters
w = -0.1
b = 3
# hype-parameters
lr = 0.00001 # 学习率
N = 100
for j in range(N):
sum_w = 0.0
sum_b = 0.0
for i in range(n_train):
y_hat = np.array(w) * x_train[i] + b
sum_w += (y_train[i] - y_hat) * (-x_train[i])
sum_b += (y_train[i] - y_hat) * (-1)
det_w = 2 * sum_w
det_b = 2 * sum_b
w = w - lr * det_w
b = b - lr * det_b
fig, ax = plt.subplots()
ax.scatter(x_train, y_train)
ax.plot([i for i in range(10, 27)], [w * i + b for i in range(10, 27)])
plt.title('y = w * x + b')
plt.legend(('Data Points', 'Model'), loc='upper left')
plt.show()
total_train_loss = 0
for i in range(n_train):
y_hat = np.array(w) * x_train[i] + b
total_train_loss += (y_train[i] - y_hat) ** 2
total_test_loss = 0
for i in range(n_test):
y_hat = np.array(w) * x_test[i] + b
total_test_loss += (y_test[i] - y_hat) ** 2
print("训练集损失值:", total_train_loss)
print("测试集损失值:", total_test_loss)
二次模型
import math
import numpy as np
import matplotlib.pyplot as plt
# 数据集
x = [12.3, 14.3, 14.5, 14.8, 16.1, 16.8, 16.5, 15.3, 17.0, 17.8, 18.7, 20.2, 22.3, 19.3, 15.5, 16.7, 17.2, 18.3, 19.2, 17.3, 19.5, 19.7, 21.2, 23.04, 23.8, 24.6, 25.2, 25.7, 25.9, 26.3]
y = [11.8, 12.7, 13.0, 11.8, 14.3, 15.3, 13.5, 13.8, 14.0, 14.9, 15.7, 18.8, 20.1, 15.0, 14.5, 14.9, 14.8, 16.4, 17.0, 14.8, 15.6, 16.4, 19.0, 19.8, 20.0, 20.3, 21.9, 22.1, 22.4, 22.6]
# print(len(x))
# 分隔训练集和测试集
x_train = x[0: 20]
y_train = y[0: 20]
n_train = len(x_train)
x_test = x[20:]
y_test = y[20:]
n_test = len(x_test)
# Fit model y = w1 * x + w2 * (x^2) + b
# 初始值
# parameters
w1 = -0.1
w2 = 0.3
b = 3
# hype-parameters
lr = 0.0000001 # 学习率
N = 100000
for j in range(N):
sum_w1 = 0.0
sum_w2 = 0.0
sum_b = 0.0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + np.array(w2) * (x_train[i] ** 2) + b
sum_w1 += (y_train[i] - y_hat) * (-x_train[i])
sum_w2 += (y_train[i] - y_hat) * (-x_train[i] ** 2)
sum_b += (y_train[i] - y_hat) * (-1)
det_w1 = 2 * sum_w1
det_w2 = 2 * sum_w2
det_b = 2 * sum_b
w1 = w1 - lr * det_w1
w2 = w2 - lr * det_w2
b = b - lr * det_b
fig, ax = plt.subplots()
ax.scatter(x_train, y_train)
ax.plot([i for i in range(10, 27)], [w1 * i + w2 * (i ** 2) + b for i in range(10, 27)])
plt.title('y = w1 * x + w2 * (x^2) + b')
plt.legend(('Data Points', 'Model'), loc='upper left')
plt.show()
total_train_loss = 0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + w2 * (x_train[i] ** 2) + b
total_train_loss += (y_train[i] - y_hat) ** 2
total_test_loss = 0
for i in range(n_test):
y_hat = np.array(w1) * x_test[i] + w2 * (x_test[i] ** 2) + b
total_test_loss += (y_test[i] - y_hat) ** 2
print("训练集损失值:", total_train_loss)
print("测试集损失值:", total_test_loss) # OverFitting 过拟合
二次模型 Adamgrad
import math
import numpy as np
import matplotlib.pyplot as plt
# 数据集
x = [12.3, 14.3, 14.5, 14.8, 16.1, 16.8, 16.5, 15.3, 17.0, 17.8, 18.7, 20.2, 22.3, 19.3, 15.5, 16.7, 17.2, 18.3, 19.2, 17.3, 19.5, 19.7, 21.2, 23.04, 23.8, 24.6, 25.2, 25.7, 25.9, 26.3]
y = [11.8, 12.7, 13.0, 11.8, 14.3, 15.3, 13.5, 13.8, 14.0, 14.9, 15.7, 18.8, 20.1, 15.0, 14.5, 14.9, 14.8, 16.4, 17.0, 14.8, 15.6, 16.4, 19.0, 19.8, 20.0, 20.3, 21.9, 22.1, 22.4, 22.6]
# print(len(x))
# 分隔训练集和测试集
x_train = x[0: 20]
y_train = y[0: 20]
n_train = len(x_train)
x_test = x[20:]
y_test = y[20:]
n_test = len(x_test)
# Fit model y = w1 * x + w2 * (x^2) + b
# 初始值
# parameters
w1 = -0.1
w2 = 0.3
b = 3
# hype-parameters
# lr = 0.0000001 # 学习率
# Adamgrad
lr_w1 = 0.0
lr_w2 = 0.0
lr_b = 0.0
N = 10000
for j in range(N):
sum_w1 = 0.0
sum_w2 = 0.0
sum_b = 0.0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + np.array(w2) * (x_train[i] ** 2) + b
sum_w1 += (y_train[i] - y_hat) * (-x_train[i])
sum_w2 += (y_train[i] - y_hat) * (-x_train[i] ** 2)
sum_b += (y_train[i] - y_hat) * (-1)
det_w1 = 2 * sum_w1
det_w2 = 2 * sum_w2
det_b = 2 * sum_b
lr_w1 = lr_w1 + det_w1 ** 2
lr_w2 = lr_w2 + det_w2 ** 2
lr_b = lr_b + det_b ** 2
w1 = w1 - (1 / math.sqrt(lr_w1) * det_w1)
w2 = w2 - (1 / math.sqrt(lr_w2) * det_w2)
b = b - (1 / math.sqrt(lr_b) * det_b)
fig, ax = plt.subplots()
ax.scatter(x_train, y_train)
ax.plot([i for i in range(10, 27)], [w1 * i + w2 * (i ** 2) + b for i in range(10, 27)])
plt.title('y = w1 * x + w2 * (x^2) + b')
plt.legend(('Data Points', 'Model'), loc='upper left')
plt.show()
total_train_loss = 0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + np.array(w2) * (x_train[i] ** 2) + b
total_train_loss += (y_train[i] - y_hat) ** 2
total_test_loss = 0
for i in range(n_test):
y_hat = np.array(w1) * x_test[i] + np.array(w2) * (x_test[i] ** 2) + b
total_test_loss += (y_test[i] - y_hat) ** 2
print("训练集损失值:", total_train_loss)
print("测试集损失值:", total_test_loss)
五次模型
import math
import numpy as np
import matplotlib.pyplot as plt
# 数据集
x = [12.3, 14.3, 14.5, 14.8, 16.1, 16.8, 16.5, 15.3, 17.0, 17.8, 18.7, 20.2, 22.3, 19.3, 15.5, 16.7, 17.2, 18.3, 19.2, 17.3, 19.5, 19.7, 21.2, 23.04, 23.8, 24.6, 25.2, 25.7, 25.9, 26.3]
y = [11.8, 12.7, 13.0, 11.8, 14.3, 15.3, 13.5, 13.8, 14.0, 14.9, 15.7, 18.8, 20.1, 15.0, 14.5, 14.9, 14.8, 16.4, 17.0, 14.8, 15.6, 16.4, 19.0, 19.8, 20.0, 20.3, 21.9, 22.1, 22.4, 22.6]
# print(len(x))
# 绘制数据集
# plt.scatter(x, y)
# plt.title('Dataset Samples')
# plt.xlabel('x')
# plt.ylabel('y')
# plt.show()
# 分隔训练集和测试集
x_train = x[0: 20]
y_train = y[0: 20]
n_train = len(x_train)
x_test = x[20:]
y_test = y[20:]
n_test = len(x_test)
# Fit model y = w1*x + w2*x^2 + w3*x^3 + w4*x^4 w5*x^5 + b
# 初始值
# parameters
N = 10000000
w1 = -0.1
w2 = 0.1
w3 = -0.1
w4 = 0.1
w5 = 0.1
b = 0.3
# hype-parameters
# Adamgrad
lr_w1 = 0.0
lr_w2 = 0.0
lr_w3 = 0.0
lr_w4 = 0.0
lr_w5 = 0.0
lr_b = 0.0
for j in range(N):
sum_w1 = 0.0
sum_w2 = 0.0
sum_w3 = 0.0
sum_w4 = 0.0
sum_w5 = 0.0
sum_b = 0.0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + np.array(w2) * (x_train[i] ** 2) + np.array(w3) * (x_train[i] ** 3) + np.array(w4) * (x_train[i] ** 4) + np.array(w5) * (x_train[i] ** 5) + b
sum_w1 = sum_w1 - (y_train[i] - y_hat) * (x_train[i] ** 1)
sum_w2 = sum_w2 - (y_train[i] - y_hat) * (x_train[i] ** 2)
sum_w3 = sum_w3 - (y_train[i] - y_hat) * (x_train[i] ** 3)
sum_w4 = sum_w4 - (y_train[i] - y_hat) * (x_train[i] ** 4)
sum_w5 = sum_w5 - (y_train[i] - y_hat) * (x_train[i] ** 5)
sum_b = sum_b - (y_train[i] - y_hat)
# Adamgrad
det_w1 = 2.0 * sum_w1
det_w2 = 2.0 * sum_w2
det_w3 = 2.0 * sum_w3
det_w4 = 2.0 * sum_w4
det_w5 = 2.0 * sum_w5
det_b = 2.0 * sum_b
lr_w1 = lr_w1 + det_w1 ** 2
lr_w2 = lr_w2 + det_w2 ** 2
lr_w3 = lr_w3 + det_w3 ** 2
lr_w4 = lr_w4 + det_w4 ** 2
lr_w5 = lr_w5 + det_w5 ** 2
lr_b = lr_b + det_b ** 2
w1 = w1 - (1 / math.sqrt(lr_w1) * det_w1)
w2 = w2 - (1 / math.sqrt(lr_w2) * det_w2)
w3 = w3 - (1 / math.sqrt(lr_w1) * det_w3)
w4 = w4 - (1 / math.sqrt(lr_w1) * det_w4)
w5 = w5 - (1 / math.sqrt(lr_w1) * det_w5)
b = b - (1 / math.sqrt(lr_b) * det_b)
fig, ax = plt.subplots()
ax.plot([i for i in range(28)], [w1 * i + w2 * (i ** 2) + w3 * (i ** 3) + w4 * (i ** 4) + w5 * (i ** 5) + b for i in range(28)])
ax.scatter(x_train, y_train)
plt.ylim(-30, 30)
plt.title('y = w1*x + w2*x^2 + w3*x^3 + w4*x^4 w5*x^5 + b')
plt.legend(('Data Points', 'Model'), loc='upper left')
plt.show()
total_train_loss = 0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + np.array(w2) * (x_train[i] ** 2) + w3 * (x_train[i] ** 3) + w4 * (x_train[i] ** 4) + w5 * (x_train[i] ** 5) + b
total_train_loss += (y_hat - y_train[i]) ** 2
total_test_loss = 0
for i in range(n_test):
y_hat = np.array(w1) * x_test[i] + np.array(w2) * (x_test[i] ** 2) + w3 * (x_test[i] ** 3) + w4 * (x_test[i] ** 4) + w5 * (x_test[i] ** 5) + b
total_test_loss += (y_hat - y_test[i]) ** 2
print("训练集损失值:", total_train_loss)
print("测试集损失值:", total_test_loss)
五次模型 (With Regularization)
import math
import numpy as np
import matplotlib.pyplot as plt
# 数据集
x = [12.3, 14.3, 14.5, 14.8, 16.1, 16.8, 16.5, 15.3, 17.0, 17.8, 18.7, 20.2, 22.3, 19.3, 15.5, 16.7, 17.2, 18.3, 19.2, 17.3, 19.5, 19.7, 21.2, 23.04, 23.8, 24.6, 25.2, 25.7, 25.9, 26.3]
y = [11.8, 12.7, 13.0, 11.8, 14.3, 15.3, 13.5, 13.8, 14.0, 14.9, 15.7, 18.8, 20.1, 15.0, 14.5, 14.9, 14.8, 16.4, 17.0, 14.8, 15.6, 16.4, 19.0, 19.8, 20.0, 20.3, 21.9, 22.1, 22.4, 22.6]
# print(len(x))
# 绘制数据集
# plt.scatter(x, y)
# plt.title('Dataset Samples')
# plt.xlabel('x')
# plt.ylabel('y')
# plt.show()
# 分隔训练集和测试集
x_train = x[0: 20]
y_train = y[0: 20]
n_train = len(x_train)
x_test = x[20:]
y_test = y[20:]
n_test = len(x_test)
# Fit model y = w1*x + w2*x^2 + w3*x^3 + w4*x^4 w5*x^5 + b
# 初始值
# parameters
N = 10000000
w1 = -0.1
w2 = 0.1
w3 = -0.1
w4 = 0.1
w5 = 0.1
b = 0.3
# hype-parameters
# Adamgrad
lr_w1 = 0.0
lr_w2 = 0.0
lr_w3 = 0.0
lr_w4 = 0.0
lr_w5 = 0.0
lr_b = 0.0
# HyperParameter
reg = 10000
for j in range(N):
sum_w1 = 0.0
sum_w2 = 0.0
sum_w3 = 0.0
sum_w4 = 0.0
sum_w5 = 0.0
sum_b = 0.0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + np.array(w2) * (x_train[i] ** 2) + np.array(w3) * (x_train[i] ** 3) + np.array(w4) * (x_train[i] ** 4) + np.array(w5) * (x_train[i] ** 5) + b
sum_w1 = sum_w1 - (y_train[i] - y_hat) * (x_train[i] ** 1)
sum_w2 = sum_w2 - (y_train[i] - y_hat) * (x_train[i] ** 2)
sum_w3 = sum_w3 - (y_train[i] - y_hat) * (x_train[i] ** 3)
sum_w4 = sum_w4 - (y_train[i] - y_hat) * (x_train[i] ** 4)
sum_w5 = sum_w5 - (y_train[i] - y_hat) * (x_train[i] ** 5)
sum_b = sum_b - (y_train[i] - y_hat)
# Adamgrad
det_w1 = 2.0 * sum_w1 + 2 * reg * w1
det_w2 = 2.0 * sum_w2 + 2 * reg * w2
det_w3 = 2.0 * sum_w3 + 2 * reg * w3
det_w4 = 2.0 * sum_w4 + 2 * reg * w4
det_w5 = 2.0 * sum_w5 + 2 * reg * w5
det_b = 2.0 * sum_b
lr_w1 = lr_w1 + det_w1 ** 2
lr_w2 = lr_w2 + det_w2 ** 2
lr_w3 = lr_w3 + det_w3 ** 2
lr_w4 = lr_w4 + det_w4 ** 2
lr_w5 = lr_w5 + det_w5 ** 2
lr_b = lr_b + det_b ** 2
w1 = w1 - (1 / math.sqrt(lr_w1) * det_w1)
w2 = w2 - (1 / math.sqrt(lr_w2) * det_w2)
w3 = w3 - (1 / math.sqrt(lr_w1) * det_w3)
w4 = w4 - (1 / math.sqrt(lr_w1) * det_w4)
w5 = w5 - (1 / math.sqrt(lr_w1) * det_w5)
b = b - (1 / math.sqrt(lr_b) * det_b)
fig, ax = plt.subplots()
ax.plot([i for i in range(28)], [w1 * i + w2 * (i ** 2) + w3 * (i ** 3) + w4 * (i ** 4) + w5 * (i ** 5) + b for i in range(28)])
ax.scatter(x_train, y_train)
plt.ylim(-30, 30)
plt.title('y = w1*x + w2*x^2 + w3*x^3 + w4*x^4 w5*x^5 + b (With Regularization)')
plt.legend(('Data Points', 'Model'), loc='upper left')
plt.show()
total_train_loss = 0
for i in range(n_train):
y_hat = np.array(w1) * x_train[i] + np.array(w2) * (x_train[i] ** 2) + w3 * (x_train[i] ** 3) + w4 * (x_train[i] ** 4) + w5 * (x_train[i] ** 5) + b
total_train_loss += (y_hat - y_train[i]) ** 2
total_test_loss = 0
for i in range(n_test):
y_hat = np.array(w1) * x_test[i] + np.array(w2) * (x_test[i] ** 2) + w3 * (x_test[i] ** 3) + w4 * (x_test[i] ** 4) + w5 * (x_test[i] ** 5) + b
total_test_loss += (y_hat - y_test[i]) ** 2
print("训练集损失值:", total_train_loss)
print("测试集损失值:", total_test_loss)

完整代码已上传至Github,各位下载时麻烦给个follow和star,感谢!
链接:LinearRegression 线性回归




