线性回归（Linear Regression）原理小结

本博客中使用到的完整代码请移步至: 我的github：https://github.com/qingyujean/Magic-NLPer，求赞求星求鼓励~~~

---

1. 模型函数

    m个样本，每个样本$x\text{x}x$有n个属性/特征描述，第i个样本的属性描述为：$x_i\text{xi}{x}_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})$。线性回归尝试使用属性/特征的线性组合来对 $x\text{x}x$–>$h(x\text{x}x)$进行预测，其中$h(x\text{x}x)$为连续值。即模型函数为：

$$\begin{gathered} h_{\theta }(x\text{x}x)={\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n+b \\ =>h_{\theta }(x\text{x}x)={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+...+{\theta }_n{x}_n,其中x_0=1,{\theta }_0=b \\ =>h_{\theta }(x\text{x}x)=\sum _{i=0}^n{\theta }_i{x}_i \end{gathered}$$
这里$x\text{x}x$表示一个样本，它有n个特征，表示为$(x_0,x_1,x_2,...,x_n)$，$x_0=1$。
写成矩阵形式，考虑m个样本，则X：
$$h(X\text{X}X)=X\theta \text{Xθ}X\theta$$
这里$X\text{X}X$是mx(n+1)维的矩阵，m为样本数，n为属性/特征数，$X\text{X}X$中还含有常数列向量$x_0$=1。$\theta$为(n+1)x1维向量，包含${\theta }_0$，$h_{\theta }(X\text{X}X)$为mx1维向量。

2. 损失函数

    回归任务中常用的性能度量是“均方误差”（mean squared error），也叫“平方损失”，损失函数的代数表达式可写为：
$$J({\theta }_0,{\theta }_1,...,{\theta }_n)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$
其中$\frac{1}{2}$是为了求导方便。损失函数的矩阵形式可写为（矩阵形式为简洁没有加上m，但是在实际实现loss时是计算的平均损失，要除以m，后面的矩阵形式都是如此，没有写入m）：
$$J(\theta \text{θ}\theta )=\frac{1}{2}(X\theta -y\text{Xθ−y}X\theta -y{)}^T(X\theta -y\text{Xθ−y}X\theta -y)$$

在线性回归问题下，平方损失函数是关于参数$\theta$的凸函数，即具有全局唯一极值点，也就是最优值点。那么求得极值点的位置，即可得到参数$\theta$的最优解。
损失函数手动实现：

def compute_loss(X, y, theta):
    h_x = X.dot(theta) # h=θ^T dot X, X=θ0*x0+θ1*x1
    m = y.size 
    J_loss = 1./(2*m) * np.sum(np.square(h_x-y))
    return J_loss

加载数据：

data = np.loadtxt(data_dir + 'linear_regression_data1.txt', delimiter=',')
print(data.shape) # (97, 2)
# X0 即theta0 对应的那一列
X = np.c_[np.ones(data.shape[0]), data[:,0]]# (97,)=>(97, 2)
print(X[:5], X.shape) # (97, 1)

y = np.c_[data[:,1]] # (97,)=>(97, 1)
print(y[:5], y.shape) # (97, 1)

# 绘制数据点
plt.scatter(X[:,1], y, s=30, c='r', marker='x', linewidths=1)
plt.xlim(4, 24)

输出：

(97, 2)
[[1.     6.1101]
 [1.     5.5277]
 [1.     8.5186]
 [1.     7.0032]
 [1.     5.8598]] (97, 2)
[[17.592 ]
 [ 9.1302]
 [13.662 ]
 [11.854 ]
 [ 6.8233]] (97, 1)

查看一下$\theta =[0,0]$时时的loss：

loss = compute_loss(X, y, [[0],[0]])
print(loss)

输出：

32.072733877455676

3. 学习算法

要求解使得平方损失最小化的参数$\theta$，可使用2种常用的方法来求解，最小二乘法（least squared method）和梯度下降法（gradient descent）。

3.1 梯度下降法

    损失函数$J(\theta \text{θ}\theta )=\frac{1}{2}(X\theta -y\text{Xθ−y}X\theta -y{)}^T(X\theta -y\text{Xθ−y}X\theta -y)$，令$z=X\theta -y\text{z=Xθ−y}z=X\theta -y$，则$J=\frac{1}{2}{z}^{T}z\text{J=21zTz}J=\frac{1}{2}{z}^{T}z$，其中$\theta \text{θ}\theta \to z\to J$存在链式求导关系，$\frac{\partial J(\theta )}{\partial \theta }=\frac{1}{2}(\frac{\partial z}{\partial \theta }{)}^T\frac{\partial J}{\partial z}=\frac{1}{2}{X}^T\text{XT}{X}^T(2z\text{z}z)=X^T\text{XT}{X}^T(X\theta -y\text{Xθ−y}X\theta -y)$，则$\theta$的使用梯度下降法的迭代计算公式为：
$$\theta =\theta -\alpha X^T\text{XT}{X}^T(X\theta -y\text{Xθ−y}X\theta -y)$$

梯度下降手动实现：

def gradient_descent(X, y, theta, alpha=0.01, num_iters=1000):
    m = y.size
    J_losses = [] # 存放每个step过程中loss，便于绘图查看loss随着优化更新的变化

    for _ in range(num_iters):
        # 计算model输出
        h_x = X.dot(theta) # (97,1)
        # 计算梯度并更新参数 X.T.dot(h_x-y):(2,97)x(97,1)=>(2,1)
        grad = 1./m * X.T.dot(h_x-y) # (2,1)
        theta = theta - alpha*grad # (2,1)
        # 计算损失
        J_losses.append(compute_loss(X, y, theta))

    return (theta, J_losses)

theta, J_losses = gradient_descent(X, y, [[0],[0]], num_iters=1500)
print('theta:', theta.ravel()) # 拉平 (2,1)=>(2,)

plt.plot(J_losses, label='mse_loss')
plt.xlim(0)
plt.ylabel('loss_mse(mean_square_error)')
plt.xlabel('iter_steps')
plt.legend()
plt.show()

输出：

theta: [-3.63029144  1.16636235]

参数theta已经求出，现在画出拟合的直线：

xx = np.arange(5, 25)
xx = np.c_[np.ones(len(xx)), xx]
print(xx[:5], xx.shape) # (20,2)
yy = xx.dot(theta) # (20,2)x(2,1)=>(20,1)
print(yy[:5], yy.shape)

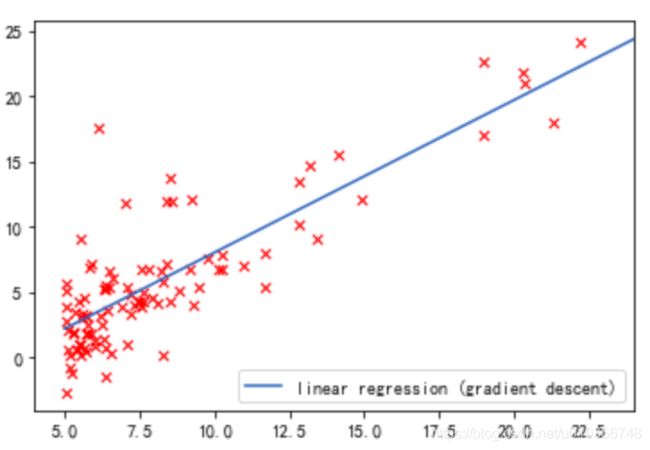
# 拟合曲线
plt.plot(xx[:,1], yy, label='linear regression (gradient descent)')
# 原始数据点
plt.scatter(X[:,1], y, s=30, c='r', marker='x', linewidths=1)

plt.xlim(4,24)
plt.legend(loc=4)
plt.show()

输出：

[[1. 5.]
 [1. 6.]
 [1. 7.]
 [1. 8.]
 [1. 9.]] (20, 2)
[[2.20152031]
 [3.36788266]
 [4.53424501]
 [5.70060736]
 [6.86696971]] (20, 1)

3.2 最小二乘法

    最小二乘法是令偏导数$\frac{\partial J(\theta )}{\partial \theta }=0$，直接求解$\theta$的表达式，由3.1可知$\frac{\partial J(\theta )}{\partial \theta }=X^T\text{XT}{X}^T(X\theta -y\text{Xθ−y}X\theta -y)$，令偏导数为0，即$X^T\text{XT}{X}^T(X\theta -y\text{Xθ−y}X\theta -y)=0$，即$X^{T}X\text{XTX}{X}^{T}X\theta \text{θ}\theta =X^{T}y\text{XTy}{X}^{T}y$，等式两边同时乘以$(X^{T}X{)}^{-1}\text{(XTX)−1}(X^{T}X{)}^{-1}$，即可得到$\theta$的使用最小二乘法的结果计算公式为：
$$\theta =(X^{T}X{)}^{-1}{X}^{T}y\text{(XTX)−1XTy}(X^{T}X{)}^{-1}{X}^{T}y$$

• 使用最小二乘法需要计算$X^{T}X\text{XTX}{X}^{T}X$的逆矩阵，矩阵可逆有条件，当不可逆时无法使用最小二乘法，此时梯度下降迭代法仍能适用。但可以通过整理样本数据，去掉冗余特征等方法，使得行列式$|X^{T}X|\ne 0$，则矩阵可逆后，再使用最小二乘法。
• 计算逆矩阵非常耗时，当特征/属性n非常大时，求n阶矩阵的逆可能不可行，此时梯度下降迭代法仍能适用。但可以通过降维的方法较少特征维度后，再使用最小二乘法。
• 如果拟合函数不是线性的，无法使用最小二乘法，此时梯度下降迭代法仍能适用；但可以通过一些技巧转化为线性问题后，再使用最小二乘法。

4. 线性回归推广

4.1 多项式回归

    以一个只有两个特征的p次方多项式回归的模型为例进行说明：
$$h_{\theta }(x_1,x_2)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2+{\theta }_5{x}_1{x}_2$$，
然后令$x_0=1,x_1=x_1,x_2=x_2,x_3=x_1^2,x_4=x_2^2,x_5=x_1{x}_2$ ,这样我们就得到了下式：
$$h_{\theta }(x_1,x_2)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+{\theta }_4{x}_4+{\theta }_5{x}_5$$
此时，一个二元的多项式回归，转化为了一个五元的线性回归，然后便可以使用线性回归的方法来完成算法。对于每个二元样本特征$(x_1,x_2)$，可转化为一个五元样本特征$(1,x_1,x_2,x_1^2,x_2^2,x_1{x}_2)$，对于转化得到的五元样本特征，便可以使用线性回归算法来求解。

sklearn.preprocessing.PolynomialFeatures的使用：
例如：有一份一个含有2元特征的数据，使用sklearn.preprocessing.PolynomialFeatures可将数据转化为28元特征的数据：

from sklearn.preprocessing import PolynomialFeatures
X = np.random.randn(100,2)
print(X.shape)
poly = PolynomialFeatures(6) # 最高次项为6次
XX = poly.fit_transform(X) # X是有2个特征，XX有28个特征（含组合特征）
print(XX.shape) # (118, 28)
# 0次项：1个，1次项：2个，2次项：3个（x1^2,x2^2,x1x2），3次项：4个
# 4次项：5个，5次项：6个，6次项：7个，一共28个特征

输出：

(100, 2)
(100, 28)

4.2 广义线性回归

4.2.1 对数线性模型（log-linear regression）

    假设输出label是在指数尺度上变化，那么可将输出label的对数作为线性模型逼近的目标，即：
$$lny\text{y}y=X\theta \text{Xθ}X\theta$$
这样得到“对数线性模型（log-linear regression）”。实际上它是在尝试让$e^{X\theta }$去逼近$y$，实际上已经是在求取输入空间到输出空间的非线性函数映射了，对数函数$ln$将线性回归模型的预测值与真实label联系起来。

4.2.2 广义线性模型（generalized linear regression）

    更一般地，考虑单调可微函数$g(\cdot )$，令
$$g(y\text{y}y)=X\theta \text{Xθ}X\theta 或y\text{y}y=g^{-1}(X\theta \text{Xθ}X\theta )$$
这样得到“广义线性模型（generalized linear regression）”。其中函数$g(\cdot )$称为联系函数，显然对数线性模型是广义线性模型在$g(\cdot )=ln(\cdot )$时的特例。

5. 加正则化项的线性回归

    为防止模型过拟合，一般会加入正则化项。线性回归的L1正则化通常称为Lasso回归，线性回归的L2正则化通常称为Ridge回归。例如这里考虑L2正则化，那么其加正则化项的损失函数代数表达式为：
$$J(\theta )=\frac{1}{2}(X\theta -y\text{Xθ−y}X\theta -y{)}^T(X\theta -y\text{Xθ−y}X\theta -y)+\frac{\lambda }{2}||\theta |{|}_2^2$$
$$即J(\theta )=\frac{1}{2}(X\theta -y\text{Xθ−y}X\theta -y{)}^T(X\theta -y\text{Xθ−y}X\theta -y)+\frac{\lambda }{2}\sum _{j=1}^n{\theta }_j^2$$
注意：正则化项中$\theta$从下标1开始计算，${\theta }_0$不参与计算。

关于正则化项的几点说明：

• 加入正则项能控制参数幅度，例如L2正则化使得参数都是较小的值（起到平滑的作用），L1正则化可直接使得某些参数为0，即某些特征的“重要性”权重为0（参数稀疏化的作用）；
• 加入正则项能限制参数搜索空间，同上，能使得参数在较小的值的范围中搜索；
• $\lambda$控制正则化的程度，$\lambda$太大会导致上式由后面部分决定，会使得$\theta \to 0$将拟合曲线拉偏，$\lambda$太小，则对参数$\theta$起不到约束作用，拟合曲线会容易被异常点/离群点拉的弯弯曲曲，不平滑；
• 正则化项其实是给参数假设一个先验分布。L1正则化等价于对参数引入拉普拉斯先验，L2正则化等价于对参数引入高斯先验。正则化参数等价于对参数引入先验分布，使得模型复杂度变小（缩小解空间），对于噪声以及 outliers 的鲁棒性增强（泛化能力）。整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计，其中正则化项对应后验估计中的先验信息，损失函数对应后验估计中的似然函数，两者的乘积即对应贝叶斯最大后验估计的形式。
• 正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大。当第一项（经验风险）较小时，模型此时一般比较复杂，此时非0参数会比较多，这时第2项的值就会较大，整体的风险（加入正则项的叫作结构风险）/损失就会大。所以第2项可以看作是对模型复杂度的惩罚项，$\lambda \ge 0$调和两者之间的关系。

6. 线性回归模型综合评价

• 形式简单，易于建模；
• 可解释性强，可控度高。$\theta$直观的表达了各特征在预测中的重要性；
• 训练快，feature engineering后效果也不错；
• 添加feature很简单；
• 蕴含了重要的基本思想，许多功能强大的非线性模型以线性模型为基础，通过引入层级结构或高维映射而得。

完整代码

完整代码请移步至: 我的github：https://github.com/qingyujean/Magic-NLPer，求赞求星求鼓励~~~

参考

[1] 机器学习（西瓜书） 周志华
[2] 线性回归原理小结   刘建平
[3] 向量/矩阵求导   刘建平
[4] 统计学习方法（第2版） 李航
[5] 正则化与数据先验分布的关系