1.插入排序
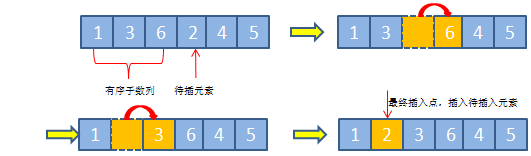
这个打麻将或者打扑克的很好理解, 比如有左手有一副牌1,2,4,7 ,来一张3的牌, 是不是就是手拿着这张牌从右往左插到2,4之间
一次插入排序的操作过程:
将待插元素,依次与已排序好的子数列元素从后到前进行比较,如果当前元素值比待插元素值大,则将移位到与其相邻的后一个位置,否则直接将待插元素插入当前元素相邻的后一位置,因为说明已经找到插入点的最终位置
public class InsertSort {
public static void sort(int[] arr) {
if (arr.length >= 2) {
for (int i = 1; i < arr.length; i++) {
//挖出一个要用来插入的值,同时位置上留下一个可以存新的值的坑
int x = arr[i];
int j = i - 1;
//在前面有一个或连续多个值比x大的时候,一直循环往前面找,将x插入到这串值前面
while (j >= 0 && arr[j] > x) {
//当arr[j]比x大的时候,将j向后移一位,正好填到坑中
arr[j + 1] = arr[j];
j--;
}
//将x插入到最前面
arr[j + 1] = x;
}
}
}
}
2.分治排序法,快速排序法
简单的说, 就是设置一个标准值, 将大于这个值的放到右边(不管排序), 将小于这个值的放到左边(不管排序), 那么这样只是区分了左小右大, 没有排序, 没关系, 左右两边再重复这个步骤.直到不能分了为止.
详细说就是:
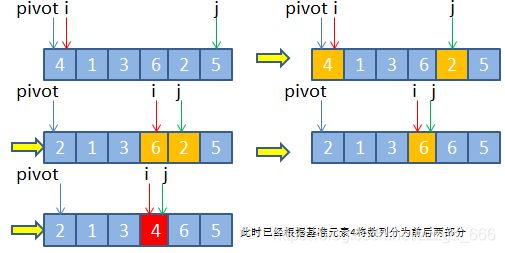
- 选择待排数列的首部第一个元素为基准元素x,设置两指针,分别指向数列首尾部位置,假设两指针分别设为i和j。
- 每次遍历的过程是这样的,首先从右到左遍历指针j所指向的元素,直到j指向的元素值小于基准元素x时,停止遍历,将其放到i的位置(因为i的值已经拷贝成了基准x腾出了位置)
- i往右挪一步, i++,接着轮到指针i从左到右遍历,直到i所指向的元素值大于基准元素x时,停止遍历,将其放到j的位置(因为上面一步j的值已经占用到了i的位置,腾出位置了)
- 依此类推,两边轮流遍历, 直到指针i与指针j相等或者大于(实际肯定是i==j)时,停止外部循环。此时必定左边都是比x小的, 右边是比x大的.
- 最后直接将基准元素x直接放置于指针i所指向的位置即可
- 完成分区操作, 从i的位置一分为二, 左边和右边再递归执行上面的操作. 层层细分
接下来,我们通过示图来展示上述分区算法思路的过程:
public class QuickSort {
public static void sort(int[] arr,int begin,int end) {
//先定义两个参数接收排序起始值和结束值
int a = begin;
int b = end;
//先判断a是否大于b
if (a >= b) {
//没必要排序
return;
}
//基准数,默认设置为第一个值
int x = arr[a];
//循环
while (a < b) {
//从后往前找,找到一个比基准数x小的值,赋给arr[a]
//如果a和b的逻辑正确--ax,就一直往下找,直到找到后面的值大于x
while (a < b && arr[b] >= x) {
b--;
}
//跳出循环,两种情况,一是a和b的逻辑不对了,a>=b,这时候排序结束.二是在后面找到了比x小的值
if (a < b) {
//将这时候找到的arr[b]放到最前面arr[a]
arr[a] = arr[b];
//排序的起始位置后移一位
a++;
}
//从前往后找,找到一个比基准数x大的值,放在最后面arr[b]
while (a < b && arr[a] <= x) {
a++;
}
if (a < b) {
arr[b] = arr[a];
//排序的终止位置前移一位
b--;
}
}
//跳出循环 a < b的逻辑不成立了,a==b重合了,此时将x赋值回去arr[a]
arr[a] = x;
//调用递归函数,再细分再排序
sort(arr,begin,a-1);
sort(arr,a+1,end);
}
}
3.冒泡排序 low版
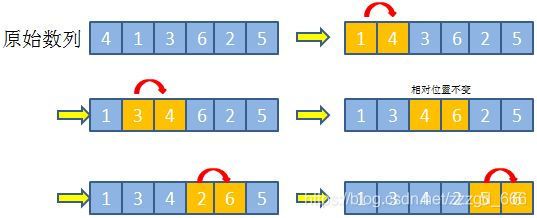
每次冒泡过程都是从数列的第一个元素开始,然后依次和剩余的元素进行比较, 跟列队一样, 从左到右两两相邻的元素比大小, 高的就和低的换一下位置. 最后最高(值最大)的肯定就排到后面了.
但是这只是把最高的排到后面了, 还得找出第二高的, 于是又从第一个开始两两比较, 高的往后站, 然后第二高的也到后面了.
然后是第三高的再往后排…
public class MaoPao {
public static void sort(int[] arr){
for (int i = 1; i < arr.length; i++) { //第一层for循环,用来控制冒泡的次数
for (int j = 0; j < arr.length-1; j++) { //第二层for循环,用来控制冒泡一层层到最后
//如果前一个数比后一个数大,两者调换 ,意味着泡泡向上走了一层
if (arr[j] > arr[j+1] ){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
4.冒泡排序 bigger版
补充, 改进后,看下文的测试结果发现提升并不大, 这是正常的, 因为改进后省略的是排序成功后的判断步骤, 而就算没改进, 排序成功后也只不过是对数组进行遍历而已, 没有进行数据更新操作, 而我们知道数组是读取快更新慢的, 所以和上面的版本相比看起来提升不算大
在这个版本中,改动了两点
- 第一点是加入了一个布尔值,判断第二层循环中的调换有没有执行,如果没有进行两两调换,说明后面都已经排好序了,已经不需要再循环了,直接跳出循环,排序结束.
- 第二点是第二层循环不再循环到arr.length - 1,因为外面的i循环递增一次,说明数组最后就多了一个排好序的大泡泡.第二层循环也就不需要到最末尾一位了,可以提前结束循环
/**
* 终极版冒泡排序
* 加入一个布尔变量,如果内循环没有交换值,说明已经排序完成,提前终止
* @param arr
*/
public static void sortPlus(int[] arr){
if(arr != null && arr.length > 1){
for(int i = 0; i < arr.length - 1; i++){
// 初始化一个布尔值
boolean flag = true;
for(int j = 0; j < arr.length - i - 1 ; j++){
if(arr[j] > arr[j+1]){
// 调换
int temp;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
// 改变flag
flag = false;
}
}
if(flag){
break;
}
}
}
}
5.选择排序
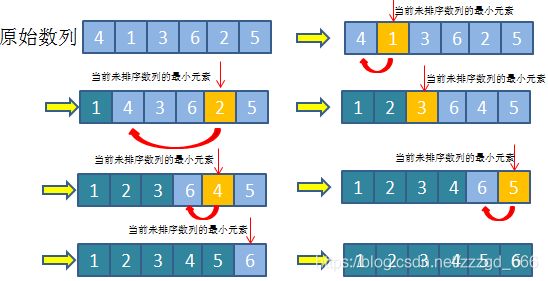
选择排序也是一种简单直观的排序算法,实现原理比较直观易懂:
首先在未排序数列中找到最小元素,然后将其与数列的首部元素进行交换,然后,在剩余未排序元素中继续找出最小元素,将其与已排序数列的末尾位置元素交换。以此类推,直至所有元素圴排序完毕.
同理,可以类比与打扑克和打麻将, 和上面插入排序不同, 插入排序相当于抽一张牌整理好了再抽一张, 而选择排序相当于一次性给你一副乱牌, 然后慢慢整理的感觉.
这也容易理解为什么选择排序为啥比插入排序慢了. 插入排序是摸一张牌, 然后直接插入到手中已经排好序的牌,再摸下一张牌.
选择排序相当于在一堆牌中, 不断的找到最小的牌往前面放.
public static void sort(int[] arr){
for(int i = 0; i < arr.length - 1 ; i++){
int min = i; // 遍历的区间最小的值
for (int j = i + 1; j < arr.length ;j++){
if(arr[j] < arr[min]){
// 找到当前遍历区间最小的值的索引
min = j;
}
}
if(min != i){
// 发生了调换
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
}
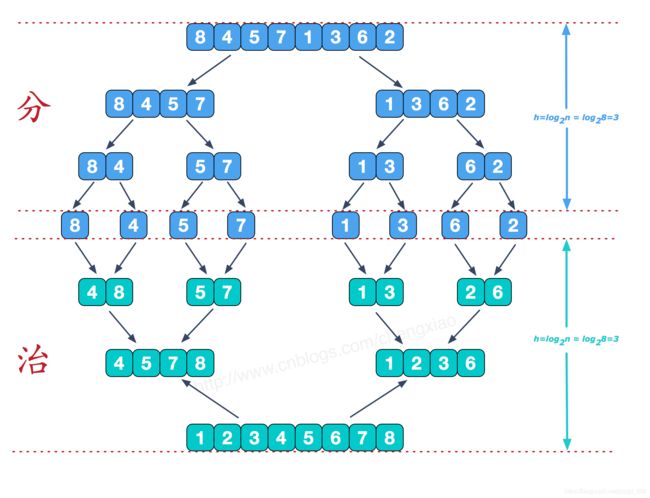
6. 归并排序
归并排序,简单的说把一串数
从中平等分为两份,再把两份再细分,直到不能细分为止. 这就是分而治之的分的步骤.
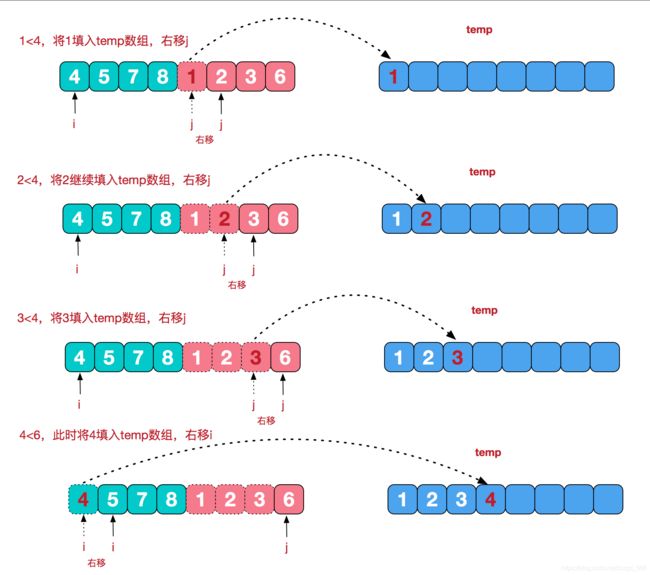
再从最小的单元,两两合并,合并的规则是将其按从小到大的顺序放到一个临时数组中,再把这个临时数组替换原数组相应位置,这就是治. 图解如下:
代码:
public static void mergeSort(int[] a,int s,int e){
int m = (s + e) / 2;
if (s < e){
mergeSort(a,s,m);
mergeSort(a,m+1,e);
//归并
merge(a,s,m,e);
}
}
private static void merge(int[] a, int s, int m, int e) {
//初始化一个从起始s到终止e的一个数组
int[] temp = new int[(e - s) + 1];
//左起始指针
int l = s;
//右起始指针
int r = m+1;
int i = 0;
//将s-e这段数据在逻辑上一分为二,l-m为一个左边的数组,r-e为一个右边的数组,两边都是有序的
//从两边的第一个指针开始遍历,将其中小的那个值放在temp数组中
while (l <= m && r <= e){
if (a[l] < a[r]){
temp[i++] = a[l++];
}else{
temp[i++] = a[r++];
}
}
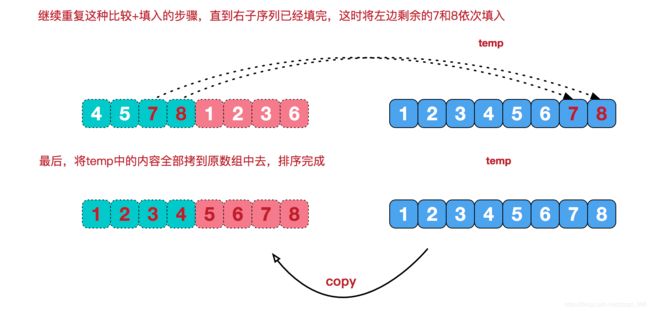
//将两个数组剩余的数放到temp中
while (l <= m){
temp[i++] = a[l++];
}
while (r <= e){
temp[i++] = a[r++];
}
//将temp数组覆盖原数组
for (int n = 0; n < temp.length; n++) {
a[s+n] = temp[n];
}
}
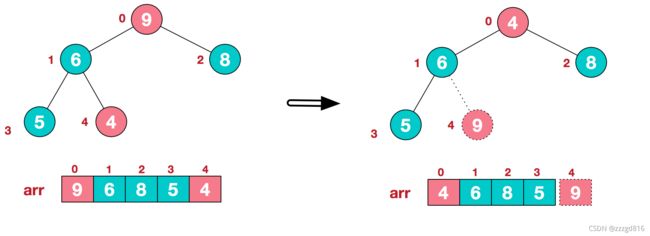
8. 堆排序
堆排序, 顾名思义, 就是将数据以堆的结构, 或者说类似于二叉树的结构, 每次都整理二叉树将最大值找到, 然后放到数组末尾. 个人感觉有点像选择排序.都是每次遍历选择一个最大值或最小值
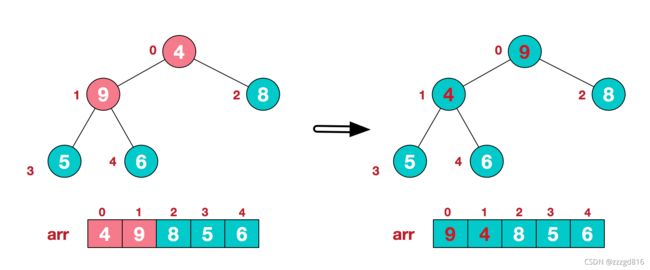
从下往上调整堆, 将最大值放到顶部
- 首先我们可以把一个数组, 从上往下, 从左到右依次放置成为二叉树
- 接着我们创建最大顶堆, 就是将最大的值调整到顶部.
- 然后我们开始遍历, 把这个[0]的最大值放到最末尾, 然后再次整理二叉树, 当然将最后一位排除在外.然后我们将截至末尾的下标往前移一位.
- 一直遍历, 把最大值放到顶部, 再调换到末尾, 到只剩最后一个元素,
找到最大值后, 放到数组后面, 并设置一个标记, 表示截止后面的都是已排序的元素, 相当于堆删除一个元素
因为是树结构, 所以整理一次树的时间复杂度是O(logn), 但是又因为它需要遍历一次挨个整理找到剩下数据中的最大值, 所以它的最坏,最好,平均时间复杂度均为O(nlogn)
踩坑
大家可以直奔v3.0版本
v1.0 巨慢不能用
这里说下踩坑, 下面是我写的堆排序v1.0版本, 写了个简单的数组测试了下发现也没有问题, ok. 然后我写一个10w的数组来和冒泡排序, 选择排序等比较, 结果发现程序像是卡死了直接花了几分钟还没出结果. 这已经远远大于冒泡排序的时间了.
/**
* 最大顶堆排序
* @param a
*/
public static void topMaxHeapSort(int[] a){
//先创建最大顶堆
createTopMaxHeap(a);
int end = a.length - 1 ;
while(end > 0 ){
//把0位的最大值放到最后
swaparr(a, 0, end);
//将计算的长度减一.不考虑最后的那个值
end--;
//重新调整堆结构
handleMaxHeapFromIndex(a, end);
}
//打印下看看
// System.out.println(Arrays.toString(a));
}
/** [3,7,1,4,9,5,6,7,2,6,8,3]
* `````````3
* ``````/ \
* `````7 1
* ````/ \ / \
* ``4 9 5 6
* `/ \ / \ /
* `7 2 6 8 3
* 变成 [9, 7, 6, 7, 6, 5, 1, 4, 2, 3, 8, 3]
* `````````9
* ```````/ \
* `````7 6
* ````/ \ / \
* ``7 6 5 1
* `/ \ / \ /
* `4 2 3 8 3
* 构建最大顶堆, 变成父节点都比子节点大的树
* @param a
*/
public static void createTopMaxHeap(int[] a){
//从倒数第二排最后一个开始, 从下往上, 层层处理把最大的换上去构建最大顶堆
//如上面的注释, 就是从5开始. 再往后就没意义了
handleMaxHeapFromIndex(a,a.length-1);
//打印下看看
// System.out.println(Arrays.toString(a));
}
private static void handleMaxHeapFromIndex(int[] a,int end){
for (int i = end / 2; i>=0; i--) {
//从i开始往后面调整它的堆
//左子节点, 右子节点
// 设置一个用于玩下遍历和判断的子节点, 默认就是左边的儿子
int child = 2 * i + 1;
while (child <= end){
//如果右子节点比左边大
int leftson = child;
int rightson = child + 1;
if(rightson <= end && a[rightson] > a[leftson]){
//就设置为右边的儿子
child++;
}
//再比较父子,如果儿子比父亲大,就互换
if(a[i] < a[child]){
swaparr(a,i,child);
}
//继续循环
i = child;
//继续选择它的左儿子
child = 2 * i + 1;
}
}
}
private static void swaparr(int[] arr,int a,int b){
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
v2.0 太慢不能用
考虑肯定调整堆的代码有问题
- 在初始构建了最大顶堆时, 父亲都比儿子大
- 后面每次都只移除顶部元素.即变化了第一层
- 那我在调整的时候, 如果这个节点比儿子节点都大, 那应该下面的都是调整好的不用管.
我选择在handleMaxHeapFromIndex方法中, 加入了break来提前跳出循环, 如下:
while (child <= end) {
// 如果右子节点比左边大
int leftson = child;
int rightson = child + 1;
if (rightson <= end && a[rightson] > a[leftson]) {
// 就设置为右边的儿子
child++;
}
// 再比较父子,如果儿子比父亲大,就互换
if (a[i] < a[child]) {
swaparr(a, i, child);
} else {
// 否则直接跳出循环, 只要父节点比子节点大, 不用管下面的调整了
break;
}
// 继续循环
i = child;
// 继续选择它的左儿子
child = 2 * i + 1;
}
再跑一次, 发现还是很慢, 但是比之前好多了, 但是还是耗时很久, 这也还是有问题啊…
v3.0
代码如下:
/**
* 最大顶堆排序
*
* @param a
*/
public static void topMaxHeapSort(int[] a) {
// 先创建最大顶堆
createTopMaxHeap(a);
System.out.println("创建完毕");
int end = a.length - 1;
while (end > 0) {
// 把0位的最大值放到最后
swaparr(a, 0, end);
// 将计算的长度减一.不考虑最后的那个值
end--;
handleMaxHeapFromIndex(a, 0, end);
}
// 打印下看看
// System.out.println(Arrays.toString(a));
}
/** [3,7,1,4,9,5,6,7,2,6,8,3]
* `````````3
* ``````/ \
* `````7 1
* ````/ \ / \
* ``4 9 5 6
* `/ \ / \ /
* `7 2 6 8 3
* 变成 [9, 7, 6, 7, 6, 5, 1, 4, 2, 3, 8, 3]
* `````````9
* ```````/ \
* `````7 6
* ````/ \ / \
* ``7 6 5 1
* `/ \ / \ /
* `4 2 3 8 3
* 构建最大顶堆, 变成父节点都比子节点大的树
* @param a
*/
public static void createTopMaxHeap(int[] a) {
// 从倒数第二排最后一个开始, 从下往上, 层层处理把最大的换上去构建最大顶堆
// 如上面的注释, 就是从5开始. 再往后就没意义了
for (int i = (a.length - 1) / 2; i >= 0; i--) {
handleMaxHeapFromIndex(a, i, a.length - 1);
}
// 打印下看看
// System.out.println(Arrays.toString(a));
}
private static void handleMaxHeapFromIndex(int[] a, int i, int end) {
// 从i开始往后面调整它的堆
// 左子节点, 右子节点
// 设置一个用于玩下遍历和判断的子节点, 默认就是左边的儿子
int child = 2 * i + 1;
while (child <= end) {
// 如果右子节点比左边大
int leftson = child;
int rightson = child + 1;
if (rightson <= end && a[rightson] > a[leftson]) {
// 就设置为右边的儿子
child++;
}
// 再比较父子,如果儿子比父亲大,就互换
if (a[i] < a[child]) {
swaparr(a, i, child);
} else {
// 否则直接跳出循环, 只要父节点比子节点大, 不用管下面的调整了
break;
}
// 继续循环
i = child;
// 继续选择它的左儿子
child = 2 * i + 1;
}
}
private static void swaparr(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
无奈之下参考了别人的博客(也有一些写的是我1.0版本和2.0版本的), 最后发现问题
首先再分析为什么要分成两步, 1. 创建大顶堆. 2. 遍历调整 ?
在创建大顶堆的时候, 是从(a.length-1)/2处从下往上整理, 才能确保最大值能像冒泡一样跑到顶部
那在构建完了大顶堆后, 我们还需不需要重新从这个位置倒排往上整理呢? 其实是不需要的. 因为变化的是第一个元素, 除了这个元素以外, 其他的元素经过大顶堆的整理肯定父亲比儿子大.
所以后面遍历调整的时候, 只需要从0下标开始找最大值就可以了. 这样就可以去掉handleMaxHeapFromIndex外层的那个循环:
private static void handleMaxHeapFromIndex(int[] a,int end){
for (int i = end / 2; i>=0; i--) { //这个循环只在创建大顶堆的时候需要, 这个就可以去掉了
....
while (child <= end){
...
}
}
另外一个坑, child<=end这里要用大于等于号, 以及后面的rightson <= end .因为我就写着写着忘记了end是最后处理的下标, 而不是数组长度, 习惯性用的<号, 导致最后2个无法排序
9. 其他排序
比如Arrays工具类提供的排序方法。它内部实现也是快速排序
private static void arraysSort(int[] a){
Arrays.sort(a);
}
还有就是将数组转为list,使用集合的排序方法,但是这无异于兜圈子,因为集合底层也是数组
private static void listSort(int[] a){
List integers = Ints.asList(a);
Collections.sort(integers);
integers.toArray(new Integer[a.length]);
}
10. 比较
试了一下几个排序的速度,代码如下:
public static void main(String[] args) {
int[] arr = new int[200000];
int[] a =getRandomArr(arr);
int[] b = a.clone();
int[] c = b.clone();
int[] d = b.clone();
int[] e = b.clone();
int[] f = b.clone();
int[] g = b.clone();
int[] h = b.clone();
long s = Clock.systemDefaultZone().millis();
quickSort(a, 0, a.length - 1);
System.out.println("quickSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
mergeSort(b,0,b.length-1);
System.out.println("mergeSort: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
listSort(c);
System.out.println("listSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
arraysSort(d);
System.out.println("arraysSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
maoPaoSort(e);
System.out.println("maoPaoSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
maoPaoSortPlus(f);
System.out.println("maoPaoSortPlus耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
insertSort(g);
System.out.println("insertSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
s = Clock.systemDefaultZone().millis();
selectSort(h);
System.out.println("selectSort耗时: " + (Clock.systemDefaultZone().millis() - s) + " ms");
}
/**
* 获取一个打乱的数组
* @param arr
*/
private static int[] getRandomArr(int[] arr) {
for (int i = 0; i < arr.length; i++) {
arr[i] = new Random().nextInt(arr.length);
}
return arr;
}
分别对1k,1w,10w,20w大小的随机数组排序,结果如下:
得到综合结果是:
速度: 快速排序>>归并排序>>>>>插入排序>>选择排序>>冒泡排序
并且可以看到,选择排序,冒泡排序在数据量越来越大的情况下,耗时已经呈指数型上涨,而不是倍数上涨,在50w的时候已经需要足足5分钟以上
//---1k---
quickSort耗时: 0 ms
mergeSort: 1 ms
listSort耗时: 7 ms
arraysSort耗时: 1 ms
maoPaoSort耗时: 3 ms
maoPaoSortPlus耗时: 4 ms
insertSort耗时: 2 ms
selectSort耗时: 3 ms
//---1w---
quickSort耗时: 2 ms
mergeSort: 3 ms
listSort耗时: 19 ms
arraysSort耗时: 4 ms
maoPaoSort耗时: 166 ms
maoPaoSortPlus耗时: 122 ms
insertSort耗时: 12 ms
selectSort耗时: 52 ms
//---10w---
quickSort耗时: 14 ms
mergeSort: 19 ms
listSort耗时: 65 ms
arraysSort耗时: 12 ms
maoPaoSort耗时: 15242 ms
maoPaoSortPlus耗时: 15044 ms
insertSort耗时: 797 ms
selectSort耗时: 4073 ms
//---20w---
quickSort耗时: 26 ms
mergeSort: 34 ms
listSort耗时: 102 ms
arraysSort耗时: 60 ms
maoPaoSort耗时: 60811 ms
maoPaoSortPlus耗时: 60378 ms
insertSort耗时: 3279 ms
selectSort耗时: 15762 ms
2021年11月25日 更新. 增加了堆排序
// 20w数据
quickSort耗时: 39 ms
mergeSort: 32 ms
创建完毕
heapSort耗时: 21 ms
listSort耗时: 111 ms
arraysSort耗时: 20 ms
maoPaoSort耗时: 50410 ms
maoPaoSortPlus耗时: 55862 ms
insertSort耗时: 10127 ms
selectSort耗时: 8619 ms
总结
到此这篇关于几种常见的java排序算法的文章就介绍到这了,更多相关java排序算法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!