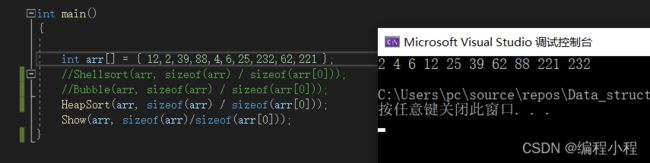
八大排序之堆排序和冒泡排序（2）

冒泡排序

排序规则

每一趟循环两两比较，大的向后挪动，最终最大值放在最后。假设现在有$n$个数据，需要跑$n-1$趟即可。

代码实现

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void Bubble(int* arr, int len)
{
	for (int i = 0; i < len - 1; i++)
	{
		for (int j = 0; j < len - i - 1; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				Swap(&arr[j], &arr[j + 1]);
			}
		}
	}
	                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                        
}

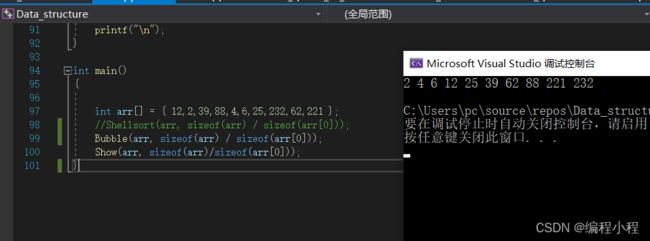
测试

算法复杂度

时间复杂度为$O(n^2)$ ，因为冒泡使用了双层for循环
空间负责度为$O(1)$，因为冒泡之使用了有限的几个变量，没有使用额外空间

堆排序

堆排序是指利用堆这种数据结构所涉及的一种排序算法，堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的索引总是小于它的父节点。

前置知识介绍

二叉树：是指树中节点的度不大于2的有序树，是由一颗由根节点和两颗互补相交的，分别被称为左子树和右子树组成的非空树。
满二叉树：如果一个二叉树只有度为0的节点和度为2的节点，并且度为0的节点在同一层，则为满二叉树。
完全二叉树:深度为k,有n个节点的二叉树当且仅当每一个节点都与深度为k的满二叉树中编号1到n的节点一一对应时，称为完全二叉树。

节点：包含一个数据元素及若干指向子树的分支信息
节点的度：一个节点拥有子树的数目称为节点的度
孩子节点：节点的子树的根称为该节点的孩子
叶子节点： 没有子树的节点或者度为0 的节点

大顶堆：父节点的值大于孩子节点
小顶堆：父节点的值小于孩子节点

算法思想

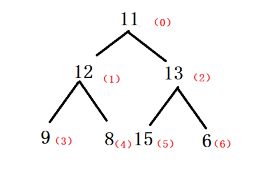
原始数据：11,12,13,9,8,15,6
若要从小到大排序，则采用大顶堆
若要从大到小排序，则采用小顶堆
以下将此采用大顶堆示例

算法步骤

1.先将数据臆想成一个完全二叉树结构

2.将其调整为大顶堆

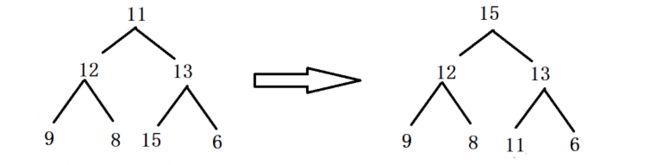
此时，我们可以发现根节点的值一定是整个数组中的最大的，并且我们知道根节点和最后一个节点的位置，我们将其位置进行交换，那么就相当于完成了冒泡排序的一次步骤。

3.将根节点的值和尾结点的值进行交换，并且将交换后尾结点的值剔除
4.重复2,3操作，直到节点只剩下一个，则结束

大顶堆调整规则

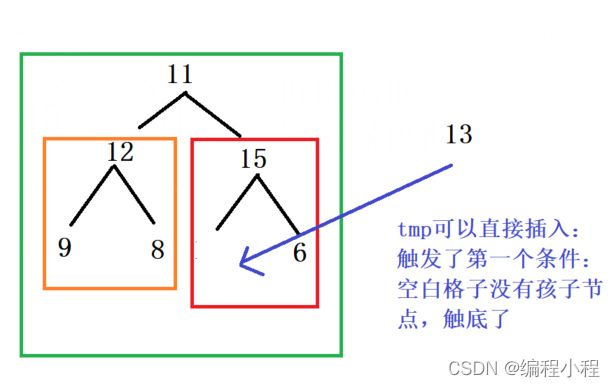
从最后一个非叶子节点开始调整（从右向左，从下到上）
调整后结果：

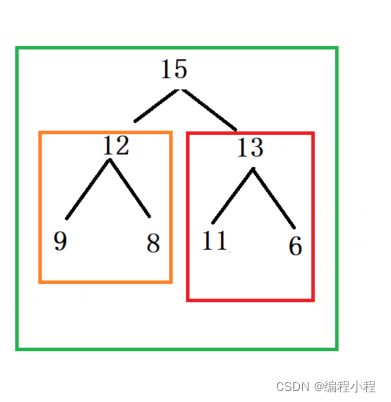
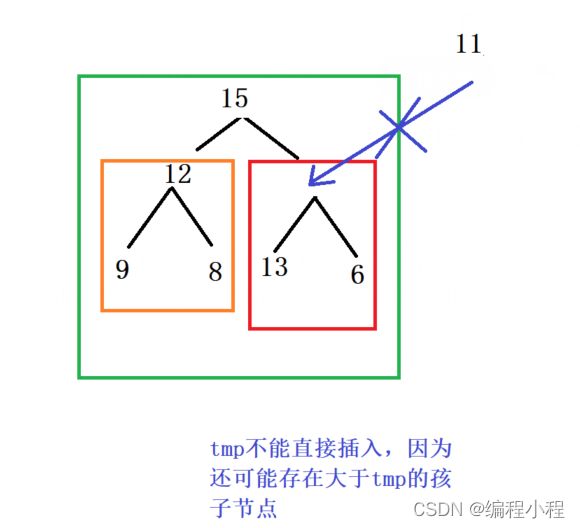
调整细节：
1.先将根节点的值取出来保存到tmp
2.需要找到当前空白节点的较大的孩子节点
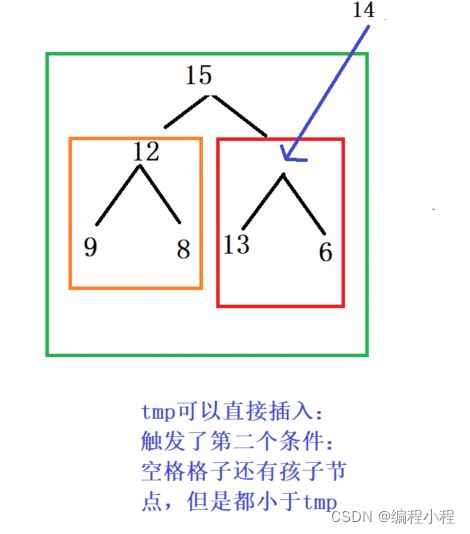
3.较大的孩子节点和tmp去比较，如果比tmp大（子大于父），则将较大的这个孩子节点向上挪动
4.孩子节点向上挪动之后，不能直接将tmp插入到原先较大孩子的位置上，因为可以它可能还有孩子节点，而这个孩子节点的值也比tmp大
5.tmp插入时间？

1）触底（较大的孩子节点没有孩子）

2）较大的孩子节点的孩子节点值都小于tmp

代码实现

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}
void heapAdjust(int *arr ,int start,int end)
{
	int tmp = arr[start];
	for (int i = start * 2 + 1; i <= end; i = start * 2 + 1) //start*2+1相当于start这个节点的左孩子
	{
		//i
		if (i<end && arr[i + 1]>arr[i])  //存在右孩子节点，并且右孩子节点值还大于左孩子节点
		{
			i++;  //此时，让i指向右孩子节点
		}

	//此时，i已经指向较大的孩子节点
		if (arr[i] > tmp)
		{
			arr[start] = arr[i];
			start = i;
		}
		else
		{
			break;  //退出for循环 ，触发情况2 
		}
	}
	arr[start] = tmp;
}
void HeapSort(int* arr, int len)
{
	//整体从最后一个非叶子节点开始由内到外调整一次
	//首先需要知道最后一个非叶子节点的下标
	for (int i = (len - 1 - 1) / 2; i >= 0; i--) //最后一个非叶子节点肯定是 最后一个叶子节点的父节点
	{
		heapAdjust(arr, i, len - 1); //调用一次调整函数
	}
	//此时，已经调整为大顶堆了
	//接下来，根节点和最后一个节点值进行交换，然后剔除掉尾结点
	for (int i = 0; i < len - 1; i++)
	{
		Swap(&arr[0], &arr[len - 1 - i]);
		heapAdjust(arr, 0, (len - 1 - i)-1);  //尾结点下标减一剔除循环
	}
}

测试

算法复杂度分析

时间复杂度：$O(nlogn)$,一次调整函数为$logn$,调用了n次。
空间复杂度：$O(1)$，因为没有用到额外空间