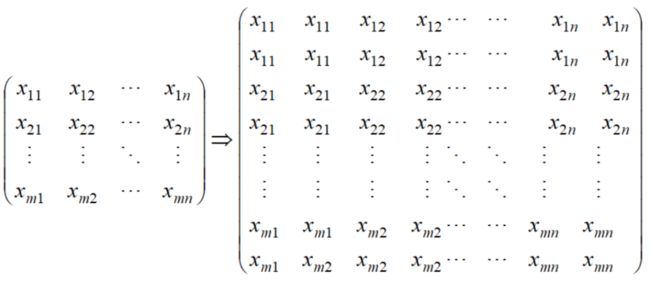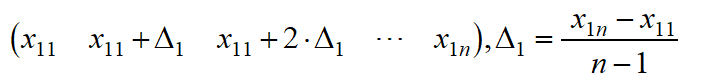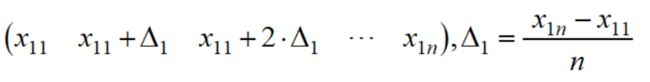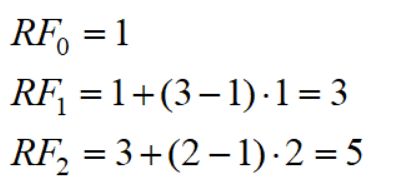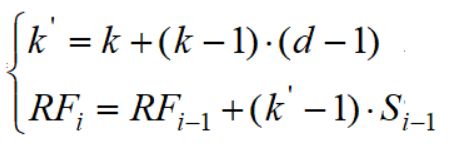理解转置卷积与空洞卷积

前两篇我们对卷积层的原理和实现做了一些介绍。这一节我们来深入了解两个常用的卷积——转置卷积和空洞卷积。

传送门：卷积核的基本概况

转置卷积

利用神经网络去生成图片，通察情况下是从低像素、粗糙的图片开始，到高像素的填充过程。这个过程就成为反卷积或者转置卷积。形象点说，反卷积是允许模型使用小图像的点“绘制”到大图像中的一个正方形。

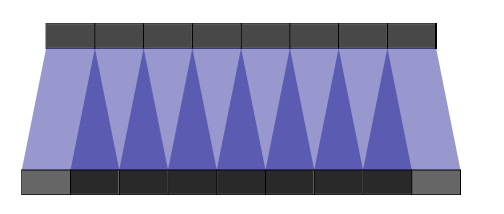
很不幸的是，这个过程会出现“不均匀重叠”现象（uneven overlap），通常称为“棋盘格伪影”：

当卷积核的边长不能被步长整除的时候出现的，下面是一个例子：

这里，下面是原始像素，上面是卷积后的像素，步长为1，卷积核为2。进行反卷积时，原图片某些位置就会被重叠。因为图片像素一般是二维的，所以有些位置重叠就会加倍，造成大小不同的棋盘式图案。

为了避免这些伪影，首先要保证卷积核大小能被步长整除，其次，最好使用步长为1的卷积核。除此之外，还有一种上采样方法可以很好避免棋盘效应——最近邻插值和双线性插值。

最近邻插值，英文是nearest-neighbor interpolation，双线性插值，英文是bilinear interpolation，它们原理比较简单，利用pytorch展示一下：

from torch.nn import UpsamplingBilinear2d
from torch.nn import UpsamplingNearest2d

input = torch.arange(1, 5, dtype=torch.float32).view(1, 1, 2, 2)
m1 = UpsamplingNearest2d(scale_factor=2)
m2 = UpsamplingBilinear2d(scale_factor=2)


m1(input)
m2(input)

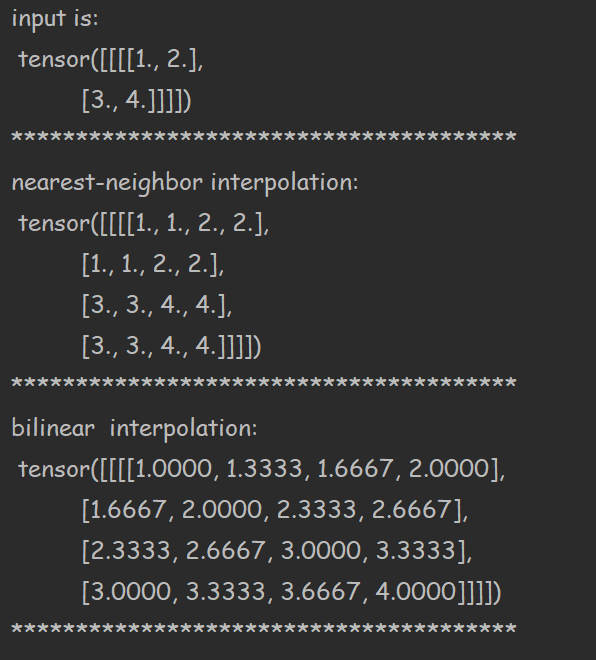
上面是把2*2卷积结果反卷积为4*4规模的，利用参数scale_factor进行缩放，也可以指定size，我们看看结果：

可以看到，最近邻插值逻辑是：

双线性插值则为，只取四个顶点作为新矩阵的值，其他值按照行列进行插值，比如第一行，插值逻辑为：

首先插值首行末行、首列末列，其他按照新插值结果再插值补充即可。

以上功能可以通过Upsample直接实现：

from torch.nn import Upsample

并且还实现了其他插值逻辑，根据参数mode和align_corners实现：

比如实现上面的双线性插值：

m3 = Upsample(scale_factor=2,mode='bilinear',align_corners=True)

如果参数align_corners设置为False，则插值逻辑是间隔的分母为行的规模：

tensorflow也可以实现相同功能，这里不再展开了。

空洞卷积

在卷积神经网络中，感受野（Receptive Field）的定义是卷积神经网络每一层输出的特征图上每个像素点在原始图像上映射的区域大小。当层感受野的公式如下：

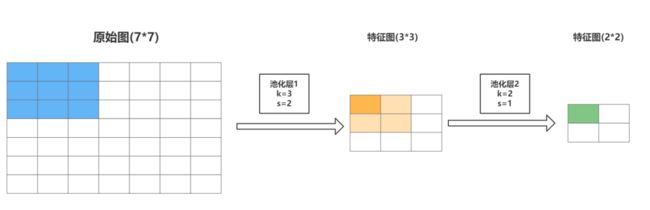
举个例子。下图是7*7的原始图片，第一层卷积层的卷积核大小3，步长2，第二层卷积层的卷积核大小为2，步长1.

原始图的每个像素就是一个感受野；图片经过第一层，输出特征图为3*3，图中深橘色的格子来自于蓝色区域，感受野为3；第二层输出特征图为2*2，绿色单元格来自于橘色区域，因此感受野为5.按照公式计算如下：

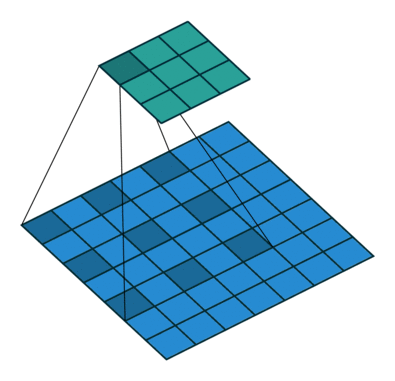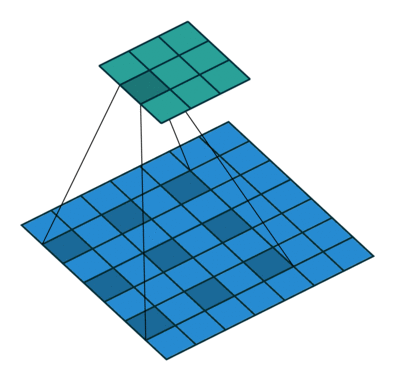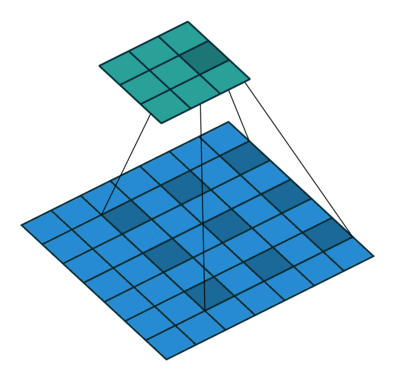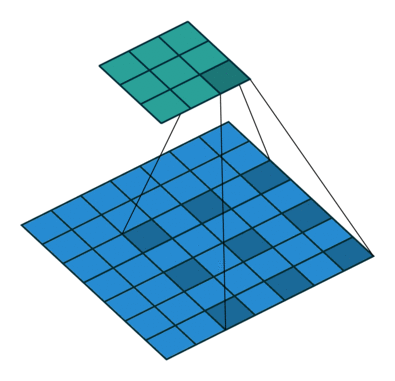
洞卷积从直观上是让卷积核膨胀的结果，下图是空洞率l=2的卷积效果：

那么空洞卷积的感受野是多少呢，很显然与普通卷积的区别在于有效卷积核大小改变了，而有效卷积核大小计算公式为：

与上面感受野公式结合起来，得到空洞卷积的感受野公式：

举个例子。

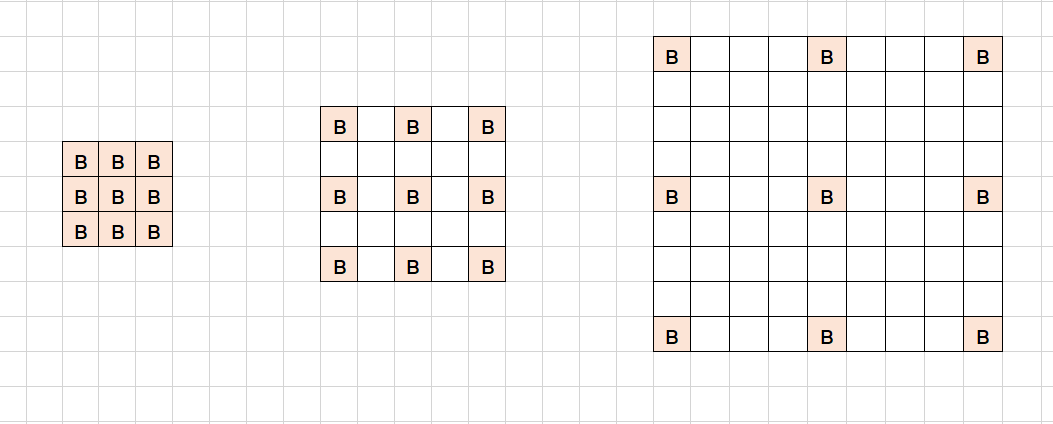
下面是三个卷积核，卷积核均为k=3,步长均为s=1，空洞卷积率分别为d=1,2,4

现在默认输入初始化感受野为1，将它们依次从左至右进行卷积，根据公式计算，每一层的感受野为：

可以看到，随着空洞率的增加，感受野会呈指数增长。但这些操作的参数数量本质上是相同的，因为卷积核大小一样，所以空洞卷积的优点是不需要增加参数运算成本就能覆盖更大的感受野。

空洞卷积针对语义分割的三个问题提出的，这里先不展开了，以后介绍到在进一步剖析，今天先理解到此。

参考链接：

https://distill.pub/2016/deconv-checkerboard/