先说结论
程序=数据结构+算法
说的直接一点就是程序设计和算法刷题这两个东西要结合着用
写在前面
数据结构和算法是每一个学计算机同学的内功和心法
无论未来从事什么岗位这两门课都绕不过去
甚至算法这门课对不学计算机的同学也同样重要
笔者在本科的时候只有数据结构这门课程,没有算法,笔者到大三的寒假参加蓝桥杯比赛才刚刚知道有算法这门课
但是笔者在备赛的时候时间仓促,没有时间去系统地学习算法
大概掌握得相对的程度也只有暴力算法,字符串专题,DFS,简单的贪心算法这四种技能
其实这个时候双非和985的区别就体现出来了
数据结构最好建立在有一定离散数学的底子的基础上,笔者学校的课程安排的不尽合理
数据结构在大二上学期就学了,但是离散数学到大二下才开始学
最重要的算法课笔者的学校更是开都没开,大概到笔者毕业的时候才刚刚开这门课
可惜开的太晚了,笔者此时已经没有时间去蹭课了
所以最重要的两门课在笔者的大学教的残缺不全
因此很长时间都云里雾里的,但是如果搞不清楚这个问题,我们就没有办法很好地去LeetCode网站刷题
这两门课笔者研究了很久,发现有些书名写着数据结构,但里面却有少许算法,但也有些书名写着算法,里面也有少许数据结构
当然更多的书是将这两门课并到一起来学习的,但实际上似乎乍看之下又没什么联系
概念
因此我们首先来看看这两门课到底是个什么东西
数据结构
数据结构其实只有三个内容:线性结构、树和图
很多同学可能会问为什么会只有这三个部分
我们先来看看数据结构的概念
我们借用一下考研大纲的概念【因为教育部发布的比较权威】
数据结构:相互之间存在一种或多种特定关系的数据元素的集合
发现没有,数据结构是一个集合,这个集合里是什么东西?
是数据元素之间的特定关系
那么既然是特定关系无非是三种:一对一,一对多,多对多
其实正好对应了三个部分
线性结构【一对一】
树型结构【一对多】
图型结构【多对多】
好,我们再拿生活当中的例子来举例
案例一:
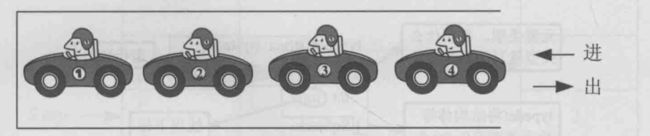
小张攒钱买了车,可是他家住在胡同的尽头。胡同很窄,只能通过一辆车,而且是死胡同,小张每天都为停车发愁,如果回家早了停在里面,早上上班就要让所有的人挪车,先让胡同口那辆出去,然后挨着一辆一辆出去,这样小张才能去上班。没办法,小张下班也不敢早回家了,等天黑了别的车都停进去了,再回去把车停在胡同口,这样早上就可以第一个去上班了。就这样,小张过起了“起早贪黑”的有车生活。
胡同很窄,只能通过一辆车, 而且是死胡同,所以只能从胡同口进出。小汽车呈线性排列,只能从一端进出,后进的汽车先出去
同学们发现没有这是什么东西?
这是典型的数据结构里面的栈
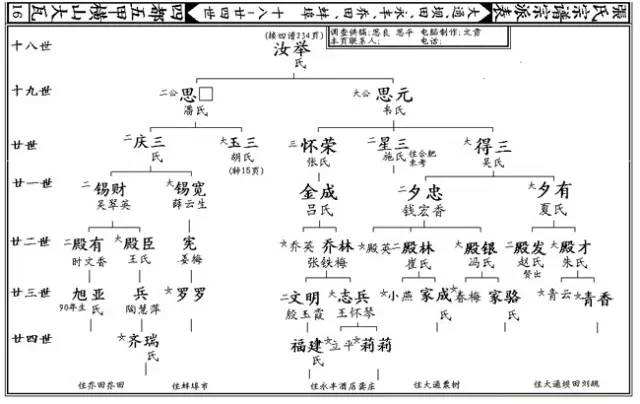
案例二:家谱
这个就更直观了,典型的树结构,事实上树形结构里的很多概念都是和家谱相似的
案例三:旅行地图
图形结构就不多做解释啦,相信大家已经可以举一反三了
同学们发现没有,数据结构的作用是干嘛,就是把我们生活中的各种复杂的现象用比较直观的关系图给我们描绘出来
说的比较功利一点,我们在刷题的时候如果搞不清楚题目里所说的各种关系,我们应当先用数据结构将它们表示出来
算法
关于算法其实并没有给出一个比较公认的定义,但是对它的含义是有一个基本的共识的
算法是一系列解决问题的明确指令,也就是说,对于符合一定规范的输入,能够在有限时间内获得要求的输出。
其实言下之意,只要能通过一系列步骤解决某种问题的都叫算法
算法本身并不是一个答案,但是用算法可以得到我们想要的答案
笔者一开始以为所有的算法已经被穷尽了,其实不是
算法是永远不可能被穷尽的,因为总有人能想出更好的办法,因此笔者在置顶博客里也告诉大家
编程能力的强弱并不是在技术而是在创意
所以很多同学在刷算法题的时候往往一下子没思路就想着去看参考答案
实际上这个做法是错误的,算法没有正确与错误一说,只有优与劣一说
事实上只要给你足够的时间,你可以用暴力算法【所谓的蛮干】解决世界上绝大多数的问题
只是暴力算法往往太慢了我们往往才另辟蹊径
情景设计
假设我们是职业小偷,背包出门偷东西
我们假设背包的承受重量是4kg
摆在我们面前的有三种商品
A.音响【3000元,4kg】
B.笔记本电脑【2000元,3kg】
C.吉他【1500元,1kg】
当然小孩子才做选择,成年人选择全都要【开个玩笑】
由于我们的背包空间是有限的,所以只能选择偷最高价值的商品
最简单的都是把所有的可能性都列出来
【1】放弃偷窃【0元,0kg】
【2】偷吉他【C】【1500元,1kg】
【3】偷音响【A】【3000元,4kg】
【4】笔记本电脑【B】【2000元,3kg】
【5】偷吉他和音响【CA】【装不下】
【6】偷吉他和笔记本电脑【CB】【3500元,4kg】
【7】偷音响和笔记本电脑【AB】【装不下】
【8】全部偷走【ABC】【装不下】
这样虽然可行,但是速度太慢了,等我们考虑完,估计警察已经在背后站半天了
放到算法时间复杂度大约是![]() ,简直慢如蜗牛
,简直慢如蜗牛
这个时候就要引出算法中的动态规划
我们先来看看动态规划算法的工作原理
动态规划简单地说就是先解决子问题,再解决母问题
当然这个概念比较难理解,请同学们慢慢看
我们回到刚才的问题
网格的各行为商品,各列为不同容量( 1~4kg)的背包。所有这些列你都需要,因为它们将帮助你计算子背包的价值。
![]()
首先来看第一行,意味着我们要尝试偷吉他【但是到底偷不偷不一定,别忘了初心,我们是为了偷走最高价值的商品】
第一个单元格表示背包的容量为一kg。
吉他的重量也是一kg,这意味着可以装入背包
![]()
这个单元格包含吉他,价值为1500美元
与这个单元格一样,每个单元格表示背包的容量为2kg,可以装下吉他
![]()
同学们可能对这个表格云里雾里,但是这里是假设只有吉他可以偷
![]()
这里同学们肯定会认为我在搞什么无聊的事情
但别忘了,我们之前说过
动态规划简单地说就是先解决子问题,再解决母问题
当前这张图是表示,如果有一个容量4kg的背包,可在其中装入的商品的最大价值为1500美元
当然肯定这不是最终的答案
接下来我们放入音响
在每一行可偷得商品都为当前行的商品以及之前各行的商品
这表示我们现在只能偷影响和吉他
![]()
第一行第一列表示
背包容量为1kg时,之前可装入商品的最大价值
第二行第一列表示
我们要用1kg的背包,在同时能偷吉他和音响的情况下,现在可装入的商品的最大价值
我们得出的结论是背包的容量只有1kg的时候,我们偷不了音响
所以这时候我们能偷的最贵东西仍然是1500元
![]()
后面的结论是一样的
![]()
到第二行第四列的时候,我们发现背包容量为4kg的时候
最大的价值更新为3000元
最后我们加入笔记本电脑
![]()
但是这时候问题来了
背包容量为3kg的时候,我们可以偷的东西选择性变大了,我们可以放弃吉他而去偷笔记本电脑,所以最大的价值更新为2000元
![]()
总算来到了最后的问题
对于容量为4kg的背包,情况很有趣
这是非常重要的部分
当前最大价值为3000元,你可以不偷音响,而偷笔记本电脑,但只价值2000元
那我们势必面临一个问题
3000元的音响 VS 2000元的笔记本电脑+1kg的空余容量
同学们发现没有,之前在1kg的容量中我们可加入的最大价值是多少?
![]()
答案是1500元
这个时候就可以作比较了
3000元【音响】 VS 2000元【笔记本电脑】+1500元【吉他】
同学们现在是否明白了为什么要计算小背包可装入了商品的最大价值
这样余下的空间我们不必再花大量的时间去做计算
![]()
答案如下,将吉他和笔记本电脑装入背包时价值最高,为3500美元
同学们听到这里可能还是有点疑惑,其实每个单元格的价值,使用的公式都相同
cell[i][j]=上一个单元的价值cell[i-1][j]VS当前商品的价值+剩余空间的价值
你可以使用这个公式来计算每个单元格的价值,最终的网格将与前一个网格相同。
现在你明白了为何要求解子问题吧?你可以合并两个子问题的解来得到更大问题的解。
想必同学们听到这里应该明白了吧,算法其实是为了帮我们更快地解决问题才用的东西【当然别算法去偷东西哈,违反乱纪的事情咱们不能干】
并且老祖宗也告诉过我们,办法总比问题多
所以没有哪个问题只有一个办法解决,只有巧办法和笨办法
算法与数据结构的应用
那肯定很多同学要问了,这两个单独拿出来我明白了,但是有什么关系呢
好,我们拿数据结构中的案例三来继续说明
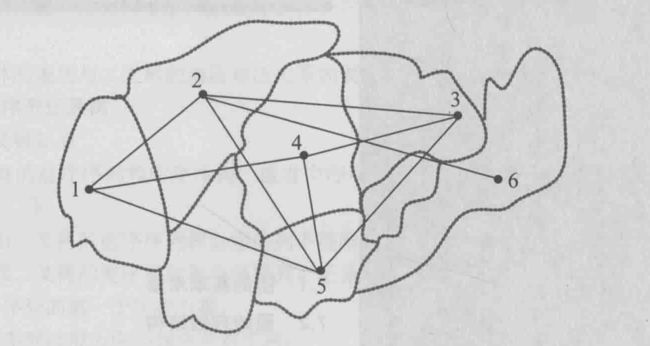
假设笔者要和一个漂亮妹妹去约会,笔者已经计划好了去这六个地方
但是呢漫长的路程不仅会耗费大量的路费,同时也会浪费很多时间在来回奔波的路上
笔者的预算和体力都比较有限,如果耗费太多所有的计划就都泡汤了
因此笔者势必要规划出一条最短的路程,这样笔者就能有足够的时间撩妹
事实上恰恰对应了算法中的最短路径算法【关于最短路径算法笔者在以后的博客里再和大家详细讨论】
同学们发现没有,笔者是在用最短路径算法之前已经无形中干了一件什么事情
没错,笔者已经构建好了一张图,在这个基础上才能规划路线
因此往往在算法之前,将每个现实生活中的一切转换成对应的数据结构就显得尤其重要
总结
只有数据结构没有算法,相当于只把数据存储到计算机中,而没有有效的方法去处理,就像一幢只有框架的烂尾楼
若只有算法,没有数据结构,就像沙漠里的海市蜃楼,只不过是空中楼阁罢了。
我们往往面对一个生活实际问题的时候先用数据结构去构建模型,再用算法在这个模型上进行一系列的操作,从而使其出现我们想要的结果