【深度学习原理第6篇】深入解析VGGNet网络+keras实现

前言

这是入门必备经典网络学习的第二篇，VGGNet由牛津大学的视觉几何组（Visual Geometry Group）和Google DeepMind公司的研究员共同提出，是以解决ImageNet比赛中的1000类图像分类和定位问题而展开的，该网络斩获2014年分类第二（第一是GoogLeNet），定位任务第一。让我们开始吧！

一、VGG网络模型结构

上图为VGG的网络结构，是作者论文中的实验图，共做了6组实验，对应6个不同的网络模型，分别是A，A-LRN，B，C，D，E。最后两组，也就是最深的两组D，E就是著名的VGG-16和VGG-19，这两组模型在分类和定位任务上的效果最好。我们再看它的网络结构，也是可以分为5个卷积部分+3个全连接，和AlexNet十分相似，很多AlexNet的影子，VGG是在它的基础上改的，可以对比学习。不太记得AlexNet可以回顾下：AlexNet网络详解

二、VGG16和VGG19网络结构分析

2.1 VGG16解析

1、首先输入的图片假设为224×224×3的彩色图片，即输入层图像矩阵大小为(224,224,3)

2、执行第一步（stage1），两个卷积块Conv1_1和Conv1_2，内含64个3×3大小的卷积核，卷积只改变通道数，64个卷积核就将矩阵变成(224,224,64)，再经过卷积核大小为2×2，步长也为2的maxpooling，对图像进行最大值池化，如下图，使得图像矩阵的长宽减半，图像变为(112,112,64)
3、执行第二步（stage2），两个卷积块Conv2_1和Conv2_2，内含128个3×3大小的卷积核，卷积后图像就变为（112，112，128），再经过卷积核大小为2×2的maxpooling，图像矩阵长宽减半，变为（56,56,128）
4、执行第三步（stage3），两个卷积块Conv3_1和Conv3_2，内含256个3×3大小的卷积核，卷积后图像就变为（58，58，256），再经过卷积核大小为2×2的maxpooling，图像矩阵长宽减半，变为（28,28,256）
5、执行第四步（stage4），两个卷积块Conv4_1和Conv4_2，内含512个3×3大小的卷积核，卷积后图像就变为（28，28，512），再经过卷积核大小为2×2的maxpooling，图像矩阵长宽减半，变为（14,14,512）
6、执行第五步（stage5），两个卷积块Conv5_1和Conv5_2，内含512个3×3大小的卷积核，卷积后图像就变为（14，14，512），再经过卷积核大小为2×2的maxpooling，图像矩阵长宽减半，变为（7,7,512）

7、执行第六步（stage6），第一个全连接将图片变为1×1×4096=4096，即（7,7,512）图像矩阵映射到4096个神经元的全连接层上，第二个再与上一个全连接进行全连接，得到神经元节点为4096的第二个全连接，最后第三个全连接，也是输出层，激活函数为softmax，可以称为softmax层，有1000个神经元节点，分别对应ImageNet竞赛数据集中1000个类别的概率。举个例子，如猫狗识别，最后只需分辨是猫还是狗两个类别，softmax层神经元节点就是2个，分别对应二者概率，若猫概率为0.76，狗概率为0.24。则认为输入的图像为猫。

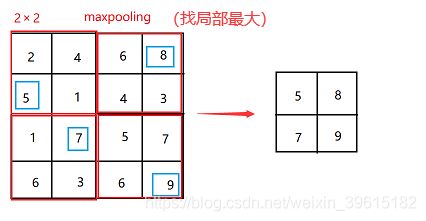
maxpooling最大值池化，从左往右stride=2，取最大值（下采样压缩过程）

2.2 VGG-19解析

VGG-19只是在stage3、4、5三个多了一个卷积块，再对特征提取了下，变化过程与VGG-16相同，一幅图说明下吧，如下。

代码实现（VGG-16为例）

#卷积块，包含Conv2D,BatchNormalization,Activation='relu'三部分
def conv_block(layer, filters, kernel_size=(3, 3), strides=(1, 1), padding='same', name=None):
    x = Conv2D(filters=filters,
               kernel_size=kernel_size,
               strides=strides,
               padding=padding,
               kernel_initializer="he_normal",
               name=name)(layer)
    x = BatchNormalization()(x)
    x = Activation('relu')(x)
    return x
    
#--------------------------
#-----stage1
#--------------------------
x = conv_block(input_layer, filters=64, kernel_size=(3, 3), name="conv1_1_64_3x3_1")
x = conv_block(x, filters=64, kernel_size=(3, 3), name="conv1_2_64_3x3_1")
x = MaxPool2D(pool_size=(2, 2), strides=(2, 2), name="max_pool_1_2x2_2")(x)

#--------------------------
#-----stage2
#--------------------------
x = conv_block(x, filters=128, kernel_size=(3, 3), name="conv2_1_128_3x3_1")
x = conv_block(x, filters=128, kernel_size=(3, 3), name="conv2_2_128_3x3_1")
x = MaxPool2D(pool_size=(2, 2), strides=(2, 2), name="max_pool_2_2x2_2")(x)

#--------------------------
#-----stage3
#--------------------------
x = conv_block(x, filters=256, kernel_size=(3, 3), name="conv3_1_256_3x3_1")
x = conv_block(x, filters=256, kernel_size=(3, 3), name="conv3_2_256_3x3_1")
x = conv_block(x, filters=256, kernel_size=(1, 1), name="conv3_3_256_3x3_1")
x = MaxPool2D(pool_size=(2, 2), strides=(2, 2), name="max_pool_3_2x2_2")(x)

#--------------------------
#-----stage4
#--------------------------
x = conv_block(x, filters=512, kernel_size=(3, 3), name="conv4_1_512_3x3_1")
x = conv_block(x, filters=512, kernel_size=(3, 3), name="conv4_2_512_3x3_1")
x = conv_block(x, filters=512, kernel_size=(1, 1), name="conv4_3_512_3x3_1")
x = MaxPool2D(pool_size=(2, 2), strides=(2, 2), name="max_pool_4_2x2_2")(x)

#--------------------------
#-----stage5
#--------------------------
x = conv_block(x, filters=512, kernel_size=(3, 3), name="conv5_1_512_3x3_1")
x = conv_block(x, filters=512, kernel_size=(3, 3), name="conv5_2_512_3x3_1")
x = conv_block(x, filters=512, kernel_size=(1, 1), name="conv5_3_512_3x3_1")
x = MaxPool2D(pool_size=(2, 2), strides=(2, 2), name="max_pool_5_2x2_2")(x)

# FC layer 1
x = Flatten()(x)
x = Dense(4096)(x)
x = BatchNormalization()(x)
x = Dropout(0.5)(x)
x = Activation("relu")(x)
    
# FC layer 2
x = Dense(4096)(x)
x = BatchNormalization()(x)
x = Dropout(0.5)(x)
x = Activation("relu")(x)
    
# FC layer 3（softmax）
x = Dense(1000)(x)
x = BatchNormalization()(x)
x = Activation("softmax")(x)

三、VGG相较AlexNet改进详解

既然VGG是在AlexNet基础上进行改进，那么主要有哪些改进，又为什么这样改呢？带着这个问题，我们来看看吧。

3.1 小卷积核

作者将卷积核全部替换为3x3（极少用了1x1），我们知道AlexNet第一层还是用了11×11的卷积核，为啥VGG要全部替换为呢？先上一幅图再来解释

设置padding=1，stride=4，output_channel=96做卷积
我们从上图可以看出不同的卷积，最后的conv+feature参数量都差不多相同，也就是说3×3，5×5，7×7，9×9，11×11，这五个不同大小的卷积，最后参数都基本持平，也就是说，总参数对性能影响不大。但是我们可以看到calc.sum这一项，卷积核越大的计算机越大，而且不是一点点，分别对应计算规模为：1600万，4500万，1.4亿、2亿。亿级别计算量是十分惊人的。这也是卷积核用小的原因，减少计算量。

先提出一个重点：多个小卷积核的堆叠比单一大卷积核精度提升更高（敲重点），下面我们来解释

如上图：这里需要谈到感受野这一概念，简单说一下
感受野是卷积神经网络每一层输出的特征图（feature map）上的像素点在输入图片上映射的区域大小。通俗点的解释是，特征图上的一个点对应输入图上的区域，这个区域就是这个点的感受野。
详细见：感受野概念详解

上图输入的8个元素可以视为feature map的宽或者高，当输入为8个神经元经过三层conv3x3的卷积得到2个神经元。三个网络分别对应stride=1，padding=0的conv3x3、conv5x5和conv7x7的卷积核在3层、1层、1层时的结果。因为这三个网络的输入都是8，也可看出：
1、2个3x3的卷积堆叠获取到的感受野大小相当于一个5x5的卷积。
2、3个3x3的卷积堆叠获取到的感受野大小相当于一个7x7的卷积。
下图为卷积后节点个数计算公式：

如3×3卷积，stride=1，padding=0，第一次卷积后得到(8+2×0-3)/1 +1=6，第二次(6-3)/1+1=4，最后一次(4-3)/1 +1=2
再如5×5卷积，stride=1，padding=0，第一次卷积（8-5）/1+1=4，效果等同两次3×3
那么7×7卷积，（8-7）/1+1=2，效果等同于3次3×3卷积

综上：由于卷积核大小越大，计算量越大，所以VGG网络用多次小卷积代替大卷积，因为多个小卷积堆叠在分类精度上比单个大卷积要好，并且计算量显著更小。

归纳一下有时面试会问到的问题：为什么用小卷积核比用大卷积核好？
1、多个小卷积核的堆叠比单一大卷积核带来了精度提升，并且感受野没有下降，计算量还减少（最重要）
2、多个小卷积核的堆叠相比较大卷积核的非线性函数会更多，更多的卷积核的使用可使决策函数更加具有辨别能力
3、卷积层的参数减少，可以回看上面给出的图，conv param部分

3.2 小池化核

相比AlexNet的kenel_size=3x3，stride=2的池化核，VGG全部为2x2的池化核，且池化的步长stride都为2，下图为3×3的maxpooling池化图，VGG中卷积核kernel size大小均为2x2，卷积核变小是为了捕获更细节的信息，即以2×2的网格从左到右、从上到下进行扫描，常见2x2的max-pooling，少见3x3或者更大的卷积核kernel。更大的kernel带来的问题是信息丢失带来的信息损失，因为如果池化的卷积核比较大的话，对应n×n网格就大，如4×4的话就是从16个里选一个最大值，这丢失的信息会较大，导致最终模型性能不高，此外，stride通常为2。

在这儿稍微补充一点：在VGG的全连接层，参数作出了些调整，高斯分布初始化（std=0.005），bias常数初始化（0.1），作者实验validate发现这个值比之前AlexNet设置的（std=0.01，bias=0）要更好。这也可以借鉴为以后调参小技巧。

3.3 层数更深特征图更宽

基于前两点外，由于卷积核专注于扩大通道数、池化专注于缩小宽和高，使得模型架构上更深更宽的同时，计算量的增加放缓，即慢慢增加，就像任务量慢慢增大；

3.4 全连接转卷积

网络测试阶段将训练阶段的三个全连接替换为三个卷积，测试重用训练时的参数，使得测试得到的全卷积网络因为没有全连接的限制，因而可以接收任意宽或高为的输入。如何理解上面这句话呢，我们来解释解释.。

上半部分是训练阶段，此时最后三层都是全连接层，下半部分是测试阶段，最后三层都是卷积层。
训练阶段
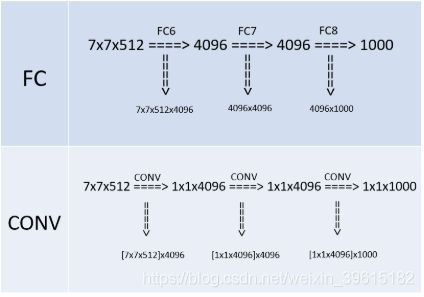
有4096个输出的全连接层FC6的输入是一个7x7x512的feature map，因为全连接层的缘故，不需要考虑局部性， 可以把7x7x512看成一个整体，25508（=7x7x512）个输入的每个元素都会与输出的每个元素（或者说是神经元）产生连接，所以每个输入都会有4096个系数对应4096个输出，所以网络的参数（也就是两层之间连线的个数，也就是每个输入元素的系数个数）规模就是7x7x512x4096。对于FC7，输入是4096个，输出是4096个，因为每个输入都会和输出相连，即每个输出都有4096条连线（系数），那么4096个输入总共有4096x4096条连线（系数），最后一个FC8计算方式一样。
预测阶段（重难点）
由于换成了卷积，第一个卷积后要得到4096（或者说是1x1x4096）的输出，那么就要对输入的7x7x512的feature map的宽高（即width、height维度）进行降维，同时对深度（即Channel/depth维度）进行升维。要把7x7降维到1x1，那么干脆直接一点，就用7x7的卷积核就行，另外深度层级的升维，因为7x7的卷积把宽高降到1x1，如下图，(7，7，512)的特征图通过和自己一摸一样大小的卷积核（7，7，512），得到一个1×1的特征图，然后有4096组，即图中绿色一直堆到红色，有4096个“神经元”，最后得到了1x1x4096的feature map。这其中卷积的参数量上，把7x7x512看做一组卷积参数，因为该层的输出是1×1×4096=4096，那么相当于要有4096组这样7x7x512的卷积参数，那么总共的卷积参数量就是[7x7x512]x4096，这里将7x7x512用中括号括起来，目的是把这看成是一组。

第二个卷积依旧得到1x1x4096的输出，因为输入也是1x1x4096，三个维度（宽、高、深）都没变化，可以很快计算出这层的卷积的卷积核大小也是1x1，而且，通道数也是4096，因为对于输入来说，1x1x4096是一组卷积参数，即一个完整的filter，那么考虑所有4096个输出的情况下，卷积参数的规模就是[1x1x4096]x4096，最后一个卷积参数[1x1x4096]x1000原理一样。

为什么要将全连接层变为卷积层？
答：对于传统的 CNN（即包含全连接层），一个确定的网络其输入图像的大小是固定的，比如 CaffeNet 的输入须是 227×227，那么对于更大的图像，在检测时就需要裁剪出很多 227×227 的小图像分别送入 CNN 网络中，使得检测任务十分耗时。
而网络需要输入固定大小图像的主要原因就是有全连接层，当把全连接层替换成了卷积层后，就可以不限制输入图像的大小，一次性输入网络即可获得一张图片所有位置的检测目标概率
固定大小是说送入网络训练的每一个数据大小需要一样，可以全都是 227×227，也可以全都是 224×224，只要统一就行。
这样要求的原因是全连接层与前一层连接时，参数数量需要预先设定好。不同于卷积操作，卷积核的参数数量就是卷积核大小，它与前一层的 特征图（feature map ）多大没有关系，但是全连接层的参数是随着前一层 feature map 的大小变化而变化的，因为与上一层全连接，当输入图像大小不同，全连接层之前得到的 feature map 大小也不一样，那么全连接层的参数数量就不能确定，所以必须固定输入图像的大小。全连接换成卷积后，带来可以处理任意分辨率（在整张图）上计算卷积，而无需对原图resize的优势。

总结：全连接变卷积就是使网络可以处理任意大小的输入图像，而无需像全连接一样必须固定输入图片的大小，不固定全连接层参数规模就无法确定。

以上就是对VGG网络的全部解析。
VGG改进详解参考：https://blog.csdn.net/jyy555555/article/details/80515562