计算机视觉算法——Transformer学习笔记

计算机视觉算法——Transformer学习笔记

清明假期被封在家里，我就利用这三天时间学习了下著名的Transfomer，参考的主要是Blibli UP主霹雳吧啦Wz的视频教程，过程有不懂的我就自己查资料，补充了一些自己的理解观点，目前还没有机会对Transformer进行实践，只是进行了简单的理论学习，有问题欢迎读者指出交流。
参考内容：
11.1 Vision Transformer(vit)网络详解
Vision Transformer 超详细解读 (原理分析+代码解读) (一)
12.1 Swin-Transformer网络结构详解

1. Vision Transformer

Transformer来源于2017年的一篇论文《Attention Is All You Need》，Transformer的提出最开始是针对NLP领域的，在此之前，NLP领域里使用的主要是RNN、LSTM这样一些网络，这些网络都存在一些问题，一方面是记忆长度有限，另一方面是无法并行，而Transeformer理论上记忆长度是无限长的，并且可以做到并行化。

而Vision Transformer是2020年发表于CVPR的论文《An Image Worth 16x16 Words: Transformers for Image Recognition as Scale》提出的，论文性能对比如下：

1.1 网络结构

Vision Transform的网络结构如下图所示：

1. 首先将输入图片切分成$16\times 16\times 3$大小的Patch，然后将Patch经过Embedding层进行编码，进行编码后每一个Patch就得到一个长度为$768\times 1$的向量，这个向量称为Token（可以理解为就是一路输入），在代码实现中中，是使用一个卷积核大小为$16\times 16$，步距为$16$的卷积核个数为$768$卷积层实现的，对于一个$244\times 244\times 3$的输入图像，通过卷积后就得到$14\times 14\times 768$特征层，然后我们将特征层的$H$和$W$方向进行展平就获得一个$196\times 768$的二维向量，也即$196$个Token。
2. 在以上基础上，再加上一个Class Token，因为以上$196$个Token输入Transformer，必然会有$196$个Token输出，我们选取哪一个作为最后的输出都不合适，因此作者Append的一路单独用于输出分类结果的Tocken，因此以上Transforer的输入就变成一个$197\times 768$的二维向量。紧接着，会进行Positional Embedding操作，这一步的具体原理可以参考关键知识点。
3. 将以上加入了Positional Embedding的$197\times 768$的二维向量输入L个堆叠的的Transformer Encoder，最后从Class Token获得输出并输入MLP Head并最终得到分类的结果。

其中，Position Encoder主要是由Norm Block、Multi-Head Attention Block和MLP Block构成，MLP Block的结构由Linear+GELU+Dropout+Linear+Dropout的结构构成，Norm Block和Multi-Head Attention的结构可以参看下面的关键知识点。
用于输出的MLP Head可以为Linear+Tanh+Linear的结构或者直接为一层Linear，具体结构可以根据不同数据集做适当改变。

论文中一共给出了三种网络结构：

其中Layer为Transform Encoder重复堆叠的个数，Hidden Size为通过Embedding层后每个Token的维度，MLP Size是Transformer Encoder中MLP Block第一个全连接的节点个数，Heads代表Mutli-Head Attention的Head数。

1.2 关键知识点

1.2.1 Self-Attention

Self-Attention是Transformer中最重要的模块之一，Self-Attention最核心的公式就是下面这三个：$$\text{ Attention }(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$$$\mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}({\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_1,\dots ,{\text{ head }}_{\mathrm{h}})W^O$$$$\text{ where head }=\text{ Attention }\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)$$下面我们先对第一个公式展开来讲，其过程分为如下图所示：

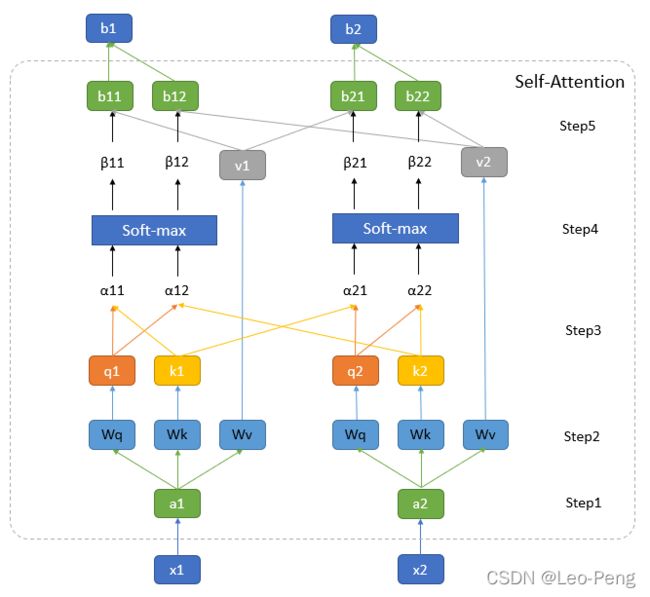
其中图中最下方的$x_1$和$x_2$为输入向量，在Vision Transformer中就是输入的图像Patch，图中最上方的$b_1$和$b_2$为经过Self-Attention编码后输出的特征，我将其中的步骤分为五步：

Step1：通过Embedding层将输入向量映射到一个更高的维度上。在Vision Transformer中这里有一层卷积层构成，这里我们可以先简单将其理解为将向量$x_1$和$x_2$映射通过某个函数$f(x)$映射到了向量$a_1$和$a_2$。

Step2：将向量向量$a_i$分别与矩阵$W_q$，$W_k$和$W_v$相乘得到$q_i$，$q_k$和$q_v$。在Vision Transformer中这里是由三个MLP组成，如果我们忽略偏置的话，我们就可以将抽象为三个矩阵，$W_q$，$W_k$和$W_v$三个矩阵的参数是可以学习的，且针对不同的$a_i$参数是共享的。
其中，$q_i$是从$a_i$中提取的用于进行匹配的向量，我们称为query。$k_i$是从$a_i$中提取的待匹配的向量，我们称为key。$v_i$是从$a_i$中提取的用于描述信息的向量，我们成为value，在接下来的步骤中我们将利用不同$a_i$query和key进行点乘获得权重，再利用该权重对value进行加权平均或者最后的输出。

Step3：依次遍历所有的$q_i$和$k_i$以$o(n^2)$的计算复杂度进行向量点乘获得${\alpha }_i$，${\alpha }_i$其实描述的是不同$a_i$之间的一种相似性，由于是点乘，这里的${\alpha }_i$已经是一个标量$${\alpha }_{1,i}=q^1\cdot k^i/\sqrt{d}$$$${\alpha }_{2,i}=q^2\cdot k^i/\sqrt{d}$$$$...$$其中$d$为向量的长度。

Step4：将${\alpha }_i$经过一个Softmax进行归一化得到${\beta }_i$，${\beta }_i$就是我们对$v_i$进行加权的权重，因为$q_i$和$k_i$都是等长的向量，因此上述Step3和Step4的操作其实就是$q_i$和$k_i$组成的两个矩阵$Q$和$K$进行矩阵乘法：$$\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)$$

Step5：${\beta }_i$与$v_i$进行加权平均就得到最后输出$b_i$，因此以上整个流程可以抽象为我们上述给出的第一个公式：$$\text{ Attention }(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$这部分操作其实就是一堆矩阵操作，如下图所示，因此可以进行GPU加速：

将上述Self-Attention的流程整理清楚后，Multi-Head Self-Attention的计算过程如下图所示：

上图展示的是head=2情况，可以看出来，所谓Multi-Head其实就是将$q_i$，$q_k$和$q_v$这几个向量均分成几部分，然后分别给计算后面的权重和加权求和结果，结构非常类似于Group卷积，最后$b_{i1}$和$b_{i2}$是通过Concatenate的操作输出的。因此Mutli-Head的计算公式为：$$\mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}({\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_1,\dots ,{\text{ head }}_{\mathrm{h}})W^O$$$$\text{ where head }=\text{ Attention }\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)$$Multi-Head的优势在哪儿呢？如下图所示，绿色的部分是一个head的query和key，而红色部分则是另一个head的query和key，我们可以看出来，红色head更关注全局信息，绿色head更关注局部信息，Multi-Head的存在其实就是是的网络更加充分地利用了输入的信息：

了解了Self-Attention的结构后，我们其实应该能够理解为什么Transformer的效果比传统的CNN效果要好，使用CNN的时候一个卷积核只能获得其感受野内的信息，而感受野的范围和大小是人为决定的，但是在Transformer中，是通过Self-Attention中去全局中搜索相关的信息，就像是感受野是的范围和大小是通过学习获得的，因此CNN可以看作是一种简化版的Transformer。

1.2.2 Positional Embedding

从上述Self-Atttention或者Mutli-Head Self-Attention的结构我们可以发现一个问题，假如由三个输入，我们修改后两个输入的顺序，对于第一个输入的结构是完全没有影响的，也就是说“我和你”和“我你和“可能表征的是同一个意思，这种问题的发生是因为Self-Attention模块的输入中并没有位置相关的信息。解决该问题的方法就是Positional Embedding，结构如下图所示：

Position Embedding结构其实就是原始的Embedding层$a_i$上加上一个Position Embedding的向量$e_i$向量，然后再送入后面的运算过程，向量$e_i$通常是人工设定的一个值，那么为什么是采用相加这种方式来表达位置关系呢？有解释如下：
假设我们给每一个位置的$x_i\in R(d,1)$并上一个One-Hot编码的向量$p_i\in R(N,1)$，得到一个新的输入向量$x_i^p\in R(d+N,1)$，然后我们乘以一个变换矩阵$W=\left[W_I,W_P\right]\in R(d,d+N)$，那么有：$$W\cdot x_i^p=\left[W_I,W_P\right]\cdot \left[\begin{array}{c}{x}_i\\ p_i\end{array}\right]=W_I\cdot x_i+W_P\cdot p_i=a_i+e_i$$因此我们可以得到一个结论，$e_i$和$a_i$相加就等于原来的输入$x_i$和表示位置的编码$p_i$进行Concatenate后再经过一个变换的结果。在Vision Transformer中通过下面这样一张图来描述训练得到的不同输入的Position Embedding向量的差异，越黄表示该输入该位置的值与该位置作为真值的余弦相似度越大：

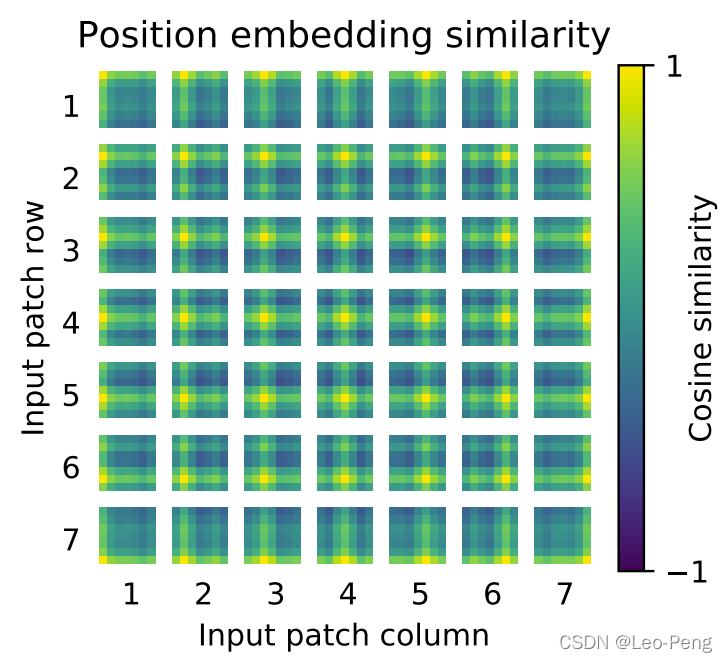
论文中还对比了加入Positional Embedding和不加入Positional Embedding的结果上的区别：
这个结果说明，加入那种形式的Positional Embedding并不重要的，关键是要加上。

1.2.3 Layer Normalization

我们比较熟悉的Batch Normalization是针对CNN设计的，其作用主要是保证输入卷积的Feature Map满足一定的分布规律，因此Batch Normalization的做法是对Feature Map的每一个维度进行标准化处理（即对某一个维度的所有通道及所有Sample的值进行标准化），而在RNN场景，同一Batch中不同Feature的维度可能是不同的，如下图所示，这就会导致**在某些维度进行标准化处理时，通道数过少甚至只有一个通道，这样统计出来的均值和方差都不能反应全局的统计分布，**因此Batch Normalization效果会变得非常差。

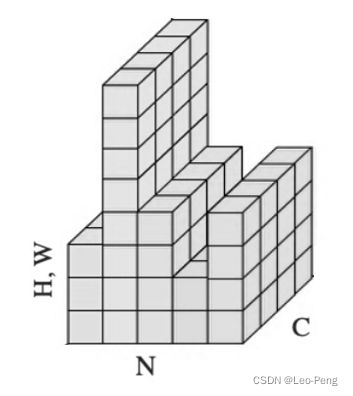
针对这个问题，由学者就提出了Layer Normalization，其和Batch Normalization的区别如下图所示：

可以看出来，Layer Normalization是针对每一个Sample进行标准化处理（及某一个Sample的所有通过维度和所有通道的值进行标注化），标准化处理的公式和Batch Normalization是一样的：$$y=\frac{x-\mathrm{E}[x]}{\sqrt{\mathrm{Var}[x]+ϵ}}\ast \gamma +\beta$$其中$\mathrm{E}[x]$为所有值的的期望，$\mathrm{Var}[x]$为所有值的方差，$\gamma$和$\beta$是可学习参数，用与恢复标准化后的特征分布。

2. Swin Transformer

Swin Transformer原论文名为《Swin Transformer: Hearchical Vision Tranformer using Shifted Windows》， 为2021年ICCV的Best Paper，Swin Tranformer和Vision Transformer的网络结构差别如下图所示：

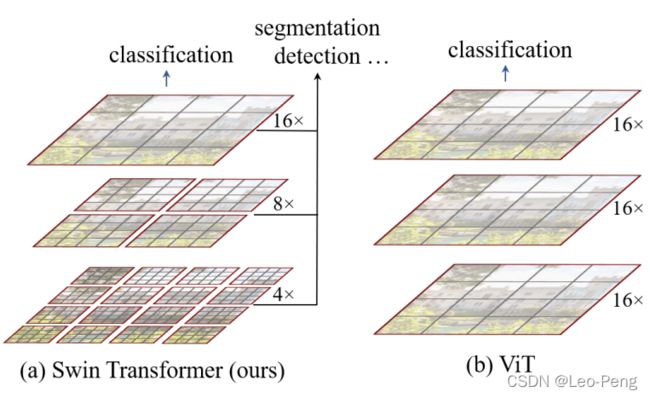
可以看到Swin Transformer具备层次结构的，每一层的特征图由一个或多个Window构成，不同层Window的大小不相同，每个Window经过Self-Attention，Window之间是不进行信息交流的；而Vision Transformer不具备层次结构且每一层都是对整个特征图进行Self-Attention。算法性能对比如下：

值得注意的一点是，Vision Transformer在ImageNet-1K的数据集上如果不经过ImageNe-22K的预训练，其效果其实是不好的，但是Swin Transfomer却能够取得很好的效果。而在FLOPs这个参数上，Swin Transformer也要优于Vision Transformer。

2.1 网络结构

Swin Transformer的网络构架如下图（a）所示：

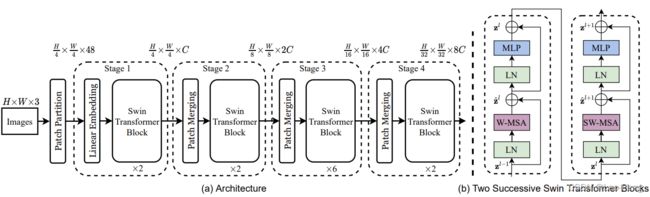
1. 图（a）中每个Swin Transfomer Block的结构包含图（b）中两种不同的结构，他们都是成对出现的，因此我们可以看到每个Swin Transfomer Block堆叠的都是偶数倍。
2. Patch Partition和Stage1模块中的Linear Embedding原理如下图所示：
   
   原图大小为$H\times W\times 3$，我们将原图拆分为16个Patch并按照深度方向进行拼接就得到$\frac{H}{4}\times \frac{W}{4}\times 48$大小的输入，然后再经过Linear Embedding层得到$\frac{H}{4}\times \frac{W}{4}\times C$大小的输入。
3. Patch Merging的主要作用是进行下采样，经过Patch Merging后，特征层高和宽会变成原来的一半，通道数翻倍，该模块原理如下：
   其中第一步是从不同的Window选择相同位置的像素组合，然后按照深度方向进行Concatenate，再经过Layer Normalization和一个线性层。

2.2 关键知识点

2.2.1 W-MSA和SW-WSA结构

W-MSA指的的Windows Multi-Head Self-Attention，前文有介绍的Multi-Head Self-Attention是在整个特征图进行计算，而W-MSA是将特征图先均分为若干个Window，在Window上作用Multi-Head Self-Attention，这样做的好处是可以减少计算量，缺点是窗口之间无法进行信息交互，导致感受野变小。这里我们分别来计算下Multi-Head Self-Attention和W-MSA的计算量区别：

首先我们知道Self-Attention公式如下：$$\mathrm{Attention}(Q,K,V)=\mathrm{SoftMax}\left(\frac{Q{K}^T}{\sqrt{d}}\right)V$$我们假设输入的输入的特征矩阵A的大小为$hw\times C$，并且我们忽略$\mathrm{SoftMax}$和$\sqrt{d}$的计算量，那么上述计算公式可以拆分成如下几步：$$A^{hw\times C}\cdot W_q^{C\times C}=Q^{hw\times C}$$$$A^{hw\times C}\cdot W_k^{C\times C}=K^{hw\times C}$$$$A^{hw\times C}\cdot W_v^{C\times C}=V^{hw\times C}$$$$Q^{hw\times C}\cdot K^{T(C\times hw)}=X^{hw\times hw}$$$$X^{hw\times hw}\cdot V^{hw\times C}=B^{hw\times C}$$我们知道对于矩阵乘法$A^{a\times b}\times B^{b\times c}$的计算量为$a\times b\times c$那么，上述三步的计算量总共是$$(hw\times C\times C)\times 3+hw\times C\times hw+hw\times hw\times C=3hw{C}^2+2(hw{)}^{2}C$$以上就是Self-Attention的计算量，在此基础上Multi-Head Self-Attention多了最后一步融合矩阵$W_o$的计算量，也就是$$B^{hw\times C}\cdot W_O^{C\times C}=O^{hw\times C}$$因此计算过量为$4hw{C}^2+2(hw{)}^{2}C$，对于W-MSA而言，由于输入被划分成了多个Window，我们假设每个Window的大小为$M\times M$，一共有$\frac{h}{M}\times \frac{w}{M}$个Window，每个Window都是Mutli-Head Self-Attention的计算量，因此总共的计算量为：$$(4(MC{)}^2+2(M{)}^{4}C)\times \frac{h}{M}\times \frac{w}{M}=4hw{C}^2+2M^{2}hwC$$综上所述：$$\Omega (\mathrm{M}\mathrm{S}\mathrm{A})=4hw{C}^2+2(hw{)}^{2}C$$$$\Omega (\mathrm{W}-\mathrm{M}\mathrm{S}\mathrm{A})=4hw{C}^2+2M^{2}hwC$$相较之下，W-MSA的计算量要小很多

SW-WSA的全称为Shifted Windows Multi-Head Self-Attention，其目的主要是实现不同窗口间的信息交互，其原理如下图所示：

其中window partition和cyclic shift的原理如下图所示：

我们以$3\times 3$的Window为例，从（a）到（b）即网格Shift的过程，Shift的大小原论文介绍是窗口大小的一半取整，因此$3\times 3$的Window为Shift大小为1，Shift完成后就得到了图（c）所示的9个Window，以最中间的Window为例，它其实是使用到了(a)中四个Window的信息，这也就是Window之间信息交互的模式，但是这样存在一个问题就是9个Window导致计算量增大，为了解决这个问题，作者将图（c）中带颜色的区域进行移动至图（d）所示，最后再重新划分4个Window如图（e）所示，这样计算量和及逆行Shift之前就完全相同。

那么还有一个问题就是图（e）这样的形态虽然对计算量有收益，但是除了左上角的Window之外，其他三个Window实际上都是由两个甚至四个子Window组成，他们不应在同一个Multi-Head Self-Attention中计算，为了解决这个问题，作者使用了masked MSA这样一个模块，实际操作将某一个特征的query和整个Window中的所有特征的key点乘后得到，在不和该特征属于同一个子Window的点乘结果上减100，这样经过Softmax后，不属于同一个子Window的权重就接近于零，后面输出也就不会用到不属于同一个子Window中的value，这样说可能会有些抽象，没理解的同学可以参考Swin-Transformer网络结构详解视频中的讲解。

在完成以上操作后，最后我们将输出的特征都恢复到原来的位置就完成整个SW-WSA的流程。可以看到，SW-WSA在不增加计算量的基础上，实现了窗口间的信息交互，这种操作确实很天才。从下图实验结果我们也可以看出来使用Shifted Windows确实可以带来较大的收益。

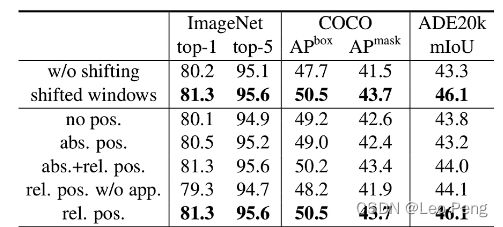
2.2.2 Relative Position Bias

Relative Position Bias指的是在Self-Attention的计算过程中，在query和key点乘后加入一个和相对位置相关的bias，其本质是希望在Attention Map能够进一步有所偏重，因此Self-Attention的公式就变成：$$\mathrm{Attention}(Q,K,V)=\mathrm{SoftMax}\left(Q{K}^T/\sqrt{d}+B\right)V$$下面我们主要来研究下这个$B\in R^{n\times n}$到底是啥，$B$并不是一个随机初始化的参数，其基本使用过程如下：

1. 初始化一个维度$(2n-1{)}^2$的Tensor作为Bias Table；
2. 构建一个从相对位置到Bias Table key的映射；
3. 前向传播中使用相对位置根据映射查询Bias Table；
4. 反向传播中更新Bias Table；

我觉得这其中最核心的部分就是就是这个相对位置到Bias Table的映射关系了，如下图所示：

首先我们将各个像素的相对位置进行二维编码$(x,y)$，其中$x$表示相对当前像素的行偏移，$y$表示相对像素的列偏移，假设Window的大小为$M\times M$，对$(x,y)$进行排列组合发现一共由$(2M-1{)}^2$种可能，这也就是为什么Bias Table的大小为$(2M-1{)}^2$，接下来我们就需要建立一个二维编码到一维编码一一对应映射关系，关系的确定一共分为三步，：

1. Step1: 将所有像素的行列编码都加上$M-1$；
2. Step2: 将所有像素的行编码相加$2M-1$；
3. Step3: 将所有像素的行列编码相加就得到最终的一维编码；

上图中的表格中的数字说明了这一变化过程，这一过程有点二进制的味道，我们可以观察下，4的左边永远是5，4的上面永远是7，这也就完成了Relative Position Bias的映射过程，接下来就去Bias Table取值更新即可，从下面这张对比表中我们可以看到，加上Relative Position Bias收益也是非常明显的：