分治法求格雷码问题_格雷码编码+解码+实现（Python）

作者：曹博

来源：微信公众号|3D视觉工坊(系投稿)

01 二值码
02 格雷码编码
2.1 编码优点
2.2 编码生成
2.3 递归生成
2.4 二值码转换
2.5 编码图
03 格雷码投影
3.1 投影图案生成
3.2 DLP投影图像
04 格雷码解码
4.1 全局/局部灰度阈值法
4.2 多幅图像阈值法
4.3 特殊情况
05 参考文献

01 二值码

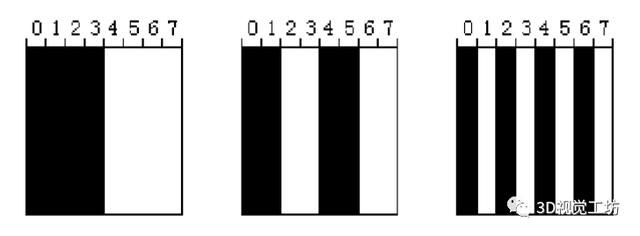
先来说结构光中最简单的情况，时域上的编码，由于极线约束的关系，我们只需要在单方向上进行编码即可，我们以最简单的两灰度级三位二进制码为例，这里有个区域，其中亮区域对应编码1，暗区域对应编码0，假设现在我们向被测物顺序投射三幅二进制编码图案，如下所示：

图1 二进制码的编码与解码原理

现在，对于这些区域，对应的编码如下：

这些区域都被我们编码起来了，没毛病！但是这样的编码虽然很简单，但是存在问题！如果和格雷码一比，你一定一眼就可以发现。

02 格雷码编码

2.1 编码优点

二进制编码缺点：相邻区域的编码的位数变化太多了！

那这会带来什么问题？当然，在相机拍照清晰的情况下，这种编码方式当然不会出现任何问题。但问题就出现在，相机拍摄到的黑白相间的边界点往往是一个过渡灰度，很容易导致解码错误(0->1 or 1->0)，这是自然二进制编码解码最容易出错的点。而格雷码最大的特定是相邻数字编码只相差一位，它们的对比如下所示：

这有什么优点呢？格雷码出错的概率更小，因为相邻区域的编码只有一位差异，有两种情况，假设编码只有一位差异，这一位错误编码出现在：

• 非差异位：对这类编码错误，我们完全可以进行补救，因为相邻两个像素的编码应该是大部分相同的，我们可以对相邻两个像素的编码进行纠正，而二进制码可没有这个编码纠正机制；
• 差异位：那无非是差一个像素而已，这时候我们无法区分这两块区域；

举个例子，对001(1)区域，它最容易出现错误的区域是黑白相间的边界处，错误的编码：011：

• 二值码：3区域，差2个像素；
• 格雷码：2区域，差1个像素，

另外，在编码的最后一幅图像里，条纹都是非常细的，以上面3位编码为例，查看编码最后位，如果是：

• 二值码：01010101
• 格雷码：01100110

由于漫反射的原因，通常容易出错的地方是黑白交错的区域解码，当条纹在最后一幅很细的时候，明显格雷码编码条纹更粗，可能出错的地方更少。

不论你是否理解，格雷码的主要优点就在于可以减小解码过程中的错误率，当然它依然有二值码一样的缺点，主要在于在选取位数较多的时候，最后几幅图的格雷码条纹会非常细，不容易分辨，因而我们通常只选取4位格雷码进行编码。这样的处理精度并不高，这也是后面我们结合相移法来进行编码、解码的主要原因。

补充：格雷码的其他应用格雷码在传统二进制控制系统中也有广泛应用，例如数字3的表示法为011，要切换为邻近的数字4，也就是 100时，装置中的三个位元都得要转换，因此于未完全转换的过程时装置会经历短暂的，010、001、101、110、111等其中数种状态，也就是代表着2、1、5、6、7，因此此种数字编码方法于邻近数字转换时有比较大的误差可能范围。但这样的转换，对于一些追求硬件性能极限的嵌入式应用，比如说飞机的电传系统中，这样的翻转来不及转换很正常！这就很尴尬！相反，格雷码只需要一位翻转即可！

2.2 编码生成

1. 改变最右边的为值；
2. 改变右边第一个为1的位元，其左边位元值；
3. 重复1、2步；

来解释下，以3位格雷码为例，从原始的值 0(000)：

1. 步骤1，改变最右边值：001
2. 步骤2，改变右边第一个为1的位元，其左边的位元：011
3. 步骤1，改变最右边值：010
4. 步骤2，改变右边第一个为1的位元，其左边的位元：110
5. 步骤1，改变最右边值：111
6. 步骤2，改变右边第一个为1的位元，其左边的位元：101

如果按照这个步骤来生成格雷码，对计算机来说，每次要去找右边第一个1，然后去翻转，其实是很麻烦的，而且这里其实有些操作是冗余的。

2.3 递归生成

我们来看格雷码其它的特点：

1. 除了最高位(左边第一位)，格雷码的位元完全对称
2. 第一个00，和最后个00；
3. 第二个01，和最后个01；
4. …
5. 而最高位的规律就更容易了，前面的格雷码为0，后面的为1

所以，格雷码的生成步骤：

1. 产生0,1两个字符串；0、1
2. 在第一步基础上：
3. 每个字符串前都+0->0+0、0+1
4. 翻转首个元素，其余对称：1+1、1+0

• 最终：00、01、11、10

1. 在上一步基础上：
2. 每个字符串前都+0->0+00、0+01、0+11、0+10
3. 翻转首字符，其余对称：1+10、1+11、1+01、1+00

• 最终：000、001、011、010、110、111、101、100

之后递归即可！我们用C++代码来实现一下，采用递归的形式：

/*==================================================@Project：GrayCode@File   : main@Desc   ：生成格雷码----------------------------------------------------@Author ：Jianbin Cao@Email  : [email protected]@Date   ：2020/11/10 20:40==================================================*/#include #include #include using namespace std;vector GrayCode(int n) {    if (n < 1) {        cout << "格雷码数量必须大于0" << endl;        assert(0);    } else if (n == 1) {        vector code;        code.emplace_back("0");        code.emplace_back("1");        return code;    } else {        vector code;        vector code_pre = GrayCode(n - 1);                for (int idx = 0; idx < code_pre.size(); ++idx) {            code.push_back("0" + code_pre[idx]);        }        for (int idx = int(code_pre.size() - 1); idx >= 0; --idx) {            code.push_back("1" + code_pre[idx]);        }        return code;    }}int main(){    int n = 4;    vector gray_code = GrayCode(n);    for (auto &g : gray_code){        cout << g << endl;    }}

2.4 二值码转换

三步：

1. 最高位保留
2. 格雷码的次高位：二进制码最高位与次高位的亦或操作；
3. 其余位的格雷码依次类推

vector GrayCode2(int n){    int count = 1 << n;    vector res(count,0);    for(int i = 1 ; i < count; i ++)    {        int bin = i,cur = bin >> (n - 1);        for(int k = n - 1;k > 0;k --)            cur = (cur << 1) + (((bin >> k) & 1) ^ ((bin >>(k - 1)) & 1));        res[i] = cur;    }    return res;}vector gray_code2 = GrayCode2(n);    for (auto &g : gray_code2){        cout << (bitset)g << endl;    }

2.5 编码图

图2 相移+格雷码编码图(查看格雷码部分)[3]

注：

03 格雷码投影

3.1 投影图案生成

结合格雷码生成和编码图，这段代码就很好写了，我们来写一下，这回我们用Python来写(人生苦短！)：

import cv2import numpy as npclass GrayCode:    codes = np.array([])    k2code = {}    k2v = {}               v2k = {}    def __init__(self, n:int=3):        self.n = n        self.codes = self.__creatCode(self.n)        # 从k(idx)转换到格雷码        for k in range(2**n):            self.k2code[k] = self.__k2code(k)        # 从格雷码转换到v        for k in range(2 ** n):            self.k2v[k] = self.__k2v(k)        # 从v转换到k(idx)        for k, v in self.k2v.items():            self.v2k[v] = k    def toPattern(self, idx:int, cols:int = 1280, rows:int = 800):        assert (idx >= 0)        row = self.codes[idx, :]        one_row = np.zeros([cols], np.uint8)        assert (cols % len(row) == 0)        per_col = int(cols / len(row))        for i in range(len(row)):            one_row[i * per_col : (i + 1) * per_col] = row[i]        pattern = np.tile(one_row, (rows, 1)) * 255        return pattern    def __creatCode(self, n:int):        code_temp = GrayCode.__createGrayCode(n)        codes = []        for row in range(len(code_temp[0])):            c = []            for idx in range(len(code_temp)):                c.append(int(code_temp[idx][row]))            codes.append(c)        return np.array(codes, np.uint8)    def __k2code(self, k):        col = self.codes[:, k]        code = ""        for i in col:            code += str(i)        return code    def __k2v(self, k):        col = list(self.codes[:, k])        col = [str(i) for i in col]        code = "".join(col)        return int(code, 2)    @staticmethod    def __createGrayCode(n:int):        if n < 1:            print("输入数字必须大于0")            assert (0);        elif n == 1:            code = ["0", "1"]            return code        else:            code = []            code_pre = GrayCode.__createGrayCode(n - 1)            for idx in range(len(code_pre)):                code.append("0" + code_pre[idx])            for idx in range(len(code_pre) - 1, -1, -1):                code.append("1" + code_pre[idx])            return codeif __name__ == '__main__':    n = 8    g = GrayCode(n)    print("code")    print(g.codes)    print("k -> code")    print(g.k2code)    print("k -> v")    print(g.k2v)    print("v -> k")    print(g.v2k)    for i in range(n):        pattern = g.toPattern(i)        title = str(i) + "-img"        cv2.imshow(title, pattern)        cv2.waitKey(0)        cv2.destroyWindow(title)

3.2 DLP投影图像

参考链接：DLP LightCrafter4500投影图像步骤整理(一)

04 格雷码解码

格雷码的解码很简单，只需要把投影的结构光还原回十进制数字，我们就能知道相机中像素点 对应于投影图片的哪一列。但现在问题的关键是，我们相机捕获回来的编码图案，由于物体材料表面反光等因素，可能暗的地方不是那么暗，亮的地方不是那么亮，这将会给正确解码工作带来一定难度！换句话说，如何对相机捕获到的结构光进行准确的二值化操作？

4.1 全局/局部灰度阈值法

最简单的方法是设置一个全局灰度阈值，对于灰度值：高于阈值的像素点：1、低于阈值的像素点：0。或者利用局部自适应阈值对图片进行二值化操作，比如：利用每个像素点周边的灰度信息进行二值化，但这类方法，由于使用结构光的环境往往是复杂的，比如说，同样的结构光，打在黑色物体表面的亮度，它就会比白色物体表面的亮度要低，这意味着同样的光条纹在不同物体上获取的灰度值不同，所以往往不能够满足格雷码解码的二值化需求！举个例子，光部分打在高反射区域(亮度高)，部分打在漫反射区域(亮度暗)，这类局部自适应阈值法就不能很好适应这种场景。

4.2 多幅图像阈值法

虽然由于环境光、以及物体表面材料原因，一副图像中像素的灰度值通常是不均匀的，我们无法直接利用一张图像中呈现的灰度信息对结构光进行解码，但是我们可以利用结构光一连串图片来帮助获取像素点当前是亮条纹还是暗条纹。

以5位的格雷码为例，其需要投影5张结构光图案：

图3 五位格雷码投影图案

假设有一个编码为11011的格雷码条纹打在物体表面上，在连续投影的5张格雷码图案中，物体表面被编码照射区域，其既经历暗条纹(编码0)，又经历亮条纹(1)，下面这条结论式确定无疑的：对于同一位置，其被亮条纹照射到的亮度总是高于其被暗条纹照射的亮度！

那么对于一个像素点在一张图片中的二值化，我们可以这样操作：首先，找到像素点在一连串格雷码图片中的最大灰度值，记为，最小灰度值，记为 ，对于每张图像，我们计算下面这个值：

图4 格雷码全暗/全亮区域[3]

因为这些点不会经历明暗变化，所以你真的不好判断是亮条纹还是暗条纹。我们有很多办法去避免这个现象，比如说：

• 避开这个编码(避开了意味着要多编码)
• 跟其他像素点亮度做比较(但是正如之前所说，由于物体表面材料属性不同，这个方法缺乏鲁棒性)

其中，有一种鲁棒性比较好的解决方法是，额外让所有编码编码位置都能经历全0或者全1的过程，这也是传统格雷码结合相移技术需要额外投射两幅全黑和全白图案的原因，如图4所示。

另外一个方法，我们额外投射一条更细的编码，如图5所示，互补格雷码结合相移。当然，实际情况当然不是不简单的多投射一条更细的格雷码这么简单，但总的来说，我们总归是有办法解决的。

图5 互补格雷码结合相移的编码图 [3]

4.3 特殊情况

但上述方法奏效的前提是，假设被亮条纹照射到的亮度总是高于该位置被暗条纹照射到的亮度。但满足这个条件的前提是：物体间没有漫反射，以及投影投射的光之间不会发生互相干扰，这在大多数情况下是成立的。但是有一些特殊的位置，有可能物体表面在亮条纹时，其亮度反而比经历暗条纹时要暗！对于这类问题，可以参考论文[1]来解决！

05 参考文献

[1]: Robust Pixel Classification for 3D Modeling with Structured Light

[2]: High-accuracy, high-speed 3D structured light imaging techniques and potential applications to intelligent robotics

[3]: 第十三公开课：基于格雷码结合相移技术的高鲁棒性高效率动态三维面形测量，四川大学，吴周杰

[4]: 系列篇|结构光——格雷码解码方法，书涵