【PyTorch】动手学深度学习-梳理与笔记小结|卷积神经网络

动手学深度学习-卷积神经网络

Refs：
参考书籍-《动手学深度学习》

从FCN到CNN

全连接层的应用背景好比是对应于一个m样本n特征属性的mxn维矩阵，在没有任何关于特征交互的先验信息情况下，去寻找特征之间的交互结构；

• 对于具有高维感知的数据，这种结构的网络无法充分利用数据中的一些先验结构；
• 例如图像数据的处理，FCN的结构也会使得模型的体量特别大。

计算机视觉的神经网络架构 v.s. 特性

• 平移不变性：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应；
• 局部性：神经网络的前面几层只探索输入图像中的局部区域，不会在意图像中相隔较远区域的关系。通过聚合这些局部特征，就可以在整个图像级别进行预测。

从数学角度理解平移不变性和局部性：

---

图像卷积

• 二维卷积层的核心计算是二维互相关运算，最简单的计算形式为——二维输入数据和卷积核执行互相关操作，添加一个偏置；
• 在DL应用过程中，通过数据驱动来学习卷积核的参数，因此无论是用严格卷积或互相关运算（两者的差别在于卷积核有无水平和垂直翻转），卷积层的输出不会受太大影响；
• 若需要检测输入中更广区域的特征，需要构建一个更深的卷积网络

卷积层及其相关运算

1. 互相关运算

import torch
from torch import nn

#在图像卷积运算中，本质上是图像和卷积核通过互相关运算得到最终结果
def corr2d(X,k):
    '''
    对给定的二维输入图像X，使用卷积核k进行卷积
    :param X: 二维图像
    :param k: 卷积核
    :return: 卷积后的二维图像
    '''
    h,w = k.shape#得到卷积核的大小
    Y = torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1))#先根据运算后的图像尺寸初始化一段空间
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j] = (X[i:i+h,j:j+w] * k).sum()#点乘取和
    return Y

#计算验证
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print('X与k进行二维卷积运算:',corr2d(X, K))

2. 自定义卷积层

卷积运算：卷积核权重和输入进行互相关运算，并在添加标量偏置之后产生输出；
可训练参数：卷积核权重，标量偏置；

训练卷积层相关模型时，随机初始化卷积核权重。

class Conv2D(nn.Module):
    def __init__(self,kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))
    
    def forward(self,x):
        return corr2d(x,self.weight)+self.bias
        #利用上面定义的互相关运算函数

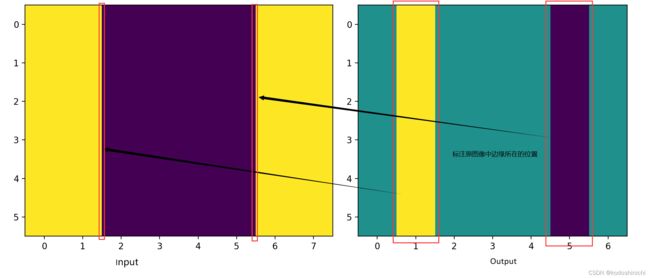
3. 二维图像中的边缘检测

• 不同的卷积核设计可以对应不同性质和类型的图像边缘；
• 原图像和边缘提取器卷积运算后的结果，可视化后就是对原图像边缘所在的位置进行了标注——
  
• 也可以通过网络来自主学习所需的卷积核参数，但同时也需要构建输入输出监督对
  

#图像边缘检测-自定义卷积核
import matplotlib.pyplot as plt

input_img = torch.ones((6,8))
input_img[:,2:6] = 0#构建了一个中间有一个宽度为4的垂直边缘的图像
print('原始的输入图像为：',input_img)
plt.imshow(input_img)
plt.show()

k = torch.tensor([[1.0,-1.0]]) #构建了一个垂直边缘卷积核
output_img = corr2d(input_img,k)
print('卷积后的输入图像为：',output_img)
plt.imshow(output_img)
plt.show()

#通过构建输入输出对，使网络自主学习卷积核
conv2d = nn.Conv2d(1,1,kernel_size=(1,2),bias = False)
#数据输入应该符合[B,C,H,W]的形式
input_img = input_img.reshape((1,1,6,8))
output_img = output_img.reshape((1,1,6,7))
lr = 3e-2

for i in range(10):
    output_img_hat = conv2d(input_img)
    loss = (output_img_hat-output_img) ** 2 #MSE Loss
    conv2d.zero_grad()
    loss.sum().backward()

    #对卷积核的参数权重迭代更新
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if(i+1) % 2 == 0:
        print(f'epoch {i+1}, loss {loss.sum(): .3f}')

new_out = conv2d(input_img).data.reshape((6,7))
print('网络学习到的卷积运算后的输出：',new_out)
plt.imshow(new_out)
plt.show()
print('网络学习到的卷积核的权重值：',conv2d.weight.data.reshape((1,2)))

4. 特征映射和感受野

【特征映射】
输出得到的卷积层有时也被称为特征映射（feature map），可以被看做从一个输入映射到下一层的空间维度的转换器；

【感受野】
对于某一层的任意元素，其感受野是指在前向传播期间可能影响x计算的所有元素（来自于先前层）；
感受野可能大于输入的实际大小，比如下图中所展示的例子所示；因此当一个特征图中的任意元素需要检测更广区域的输入特征时，可以构建一个更深的网络。

Homework

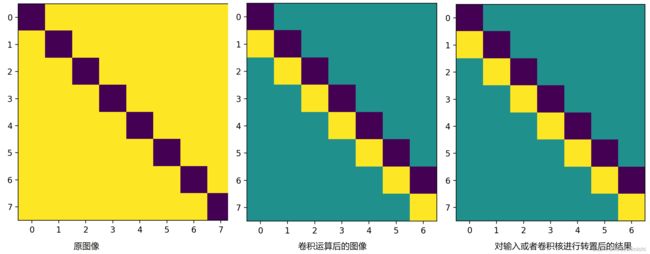
T1:对于对角线形式的边缘线，原图像的水平和竖直翻转操作并不会改变这个边缘特征的识别

T3：卷积的核心就是两个元素块求互相关运算，表现为矩阵对应位置元素相乘再相加；其也可以压缩成一维向量，然后理解成向量进行点乘再求和。因此，向量之间的点乘，可以表示为行向量和列向量的矩阵乘法运算，最后返回一个数值。

T4:参考文章-常见图像卷积核小结

# 构建具有对角线边缘的图像- T1
diag_img =  torch.ones((8,8))
# diag_img[0][0] = 0
for i in range(diag_img.shape[0]):
    diag_img[i][i] = 0
    # if i-1 and i+1<8:
    #     diag_img[i,i-1:i+2] = 0#构建了对角线为分隔界限的图像
print('原始的输入图像为：',diag_img)
plt.imshow(diag_img)
plt.show()

k = torch.tensor([[1.0,-1.0]]) #构建了一个垂直边缘卷积核
output_img = corr2d(diag_img,k)
print('卷积后的输入图像为：',output_img)
plt.imshow(output_img)
plt.show()

#转置输入图像
# plt.imshow(corr2d(diag_img.T,k))

#转置卷积核
plt.imshow(corr2d(diag_img,k.T))

#修改卷积核和输入张量，将互相关运算转变成矩阵乘法运算  -T3
#即——用矩阵乘法的形式来实现互相关运算
def corr2d_new(X,k):
    '''
    对给定的二维输入图像X，使用卷积核k进行卷积
    :param X: 二维图像
    :param k: 卷积核
    :return: 卷积后的二维图像
    '''
    h,w = k.shape#得到卷积核的大小
    Y = torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1))#先根据运算后的图像尺寸初始化一段空间
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            x = X[i:i+h,j:j+w].reshape(1,h*w)
            kk = k.reshape(h*w,1)
            Y[i,j] = torch.matmul(x,kk)#行列向量进行矩阵乘法运算
    return Y

#计算验证
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print('X与k进行二维卷积运算:',corr2d_new(X, K))

---

填充和步幅

Tips

①卷积运算的输出大小取决于输入形状、卷积核的形状，以及填充和步幅的大小；

②填充——
当输出的尺寸相较于输入较少时，我们丢失了原始图像边界处的信息，可以使用填充解决该问题；

③步幅——
当对于原始的输入存在分辨率有冗余的情况，我们希望能够大幅地降低图像的宽度和高度，步幅就派上用场；

填充和步幅都是用于有效调整数据的维度大小

---

多输入多输出通道

Tips

多通道输入和多输入通道卷积核之间进行二维互相关运算：
①输入数据的通道数决定了卷积核的通道数（此时卷积核可被看做是一个三维张量[channel_nums,kernel_size_height,kernel_size_width]）；
②假设输入数据和卷积核的通道数记为c_i，则可以对每个通道输入的二维张量和卷积核对应的二维张量进行互相关运算，再对通道进行求和即得到结果二维张量——即：对每个通道执行互相关操作，然后将结果相加。

在流行的神经网络架构中，随着网络层数的加深，通常会增加输出通道的维数，在减少空间分辨率的同时获得更大的通道深度——可以把每个通道看做是对不同特征的响应。

---

多通道输入和多通道输出的卷积运算：

---

1x1卷积
定义和特征：即kernel的宽和高均只有一个单位，它失去了卷积运算的本质特点——有效提取相邻像素间的相关特征；

作用：1x1卷积依然十分流行，经常包含在复杂的深层网络设计中，它的计算发生在通道的维度上——也就是将各个通道上对应像素点上的值进行一个累加，可以将其看做是在每个像素位置应用的全连接层，只不过对于不同的像素点采取的是同样的全连接层结构和权值（卷积运算共享权重的特点）

Codes&Homework

T1：多个卷积在运算中可以等价表示成输出数据有多通道，因此分别用kernel1和kernel2进行两次卷积计算，就等价于用一个(2,kernel_height,kernel_width)的三维卷积核进行一次运算。
p.s 需要两个卷积核具有相同的尺寸;

T2:计算复杂度计算（摘自评论区）

T3：若输入通道和输出通道的数量够分别扩大到p和q倍，则计算数量会扩大到p*q倍；
若卷积运算中padding的数量扩大到其自身的两倍，计算量会扩大到4倍

T4:若卷积核是1x1的，那么前向传播计算的复杂度是O(C~in~ x C~out~ x Input~width~ x Input~height~).

T5:Y1和Y2首先不是同一个变量，其次其数值也不一定能够相同，因为输入数据和卷积核都是浮点类型。

T6：即使卷积窗口不是1x1，卷积的内核运算是互相关，而两个矩阵额点乘求和本身就是可以转换成向量（需要先拉成/平铺成一个向量）的点乘，也就是一个行向量和一个列向量的矩阵乘法运算——这说明从理论上卷积和矩阵乘法是可以等价的；在实际实现中，需要将二维卷积核展开成一维向量，每次从输入数据中取得的同尺寸样本也需要展开成向量。

import torch

def corr2d(X,k):
    '''
    对给定的二维输入图像X，使用卷积核k进行卷积
    :param X: 二维图像
    :param k: 卷积核
    :return: 卷积后的二维图像
    '''
    h,w = k.shape#得到卷积核的大小
    Y = torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1))#先根据运算后的图像尺寸初始化一段空间
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j] = (X[i:i+h,j:j+w] * k).sum()#点乘取和
    return Y

def corr2d_multi_in(X,K):
    '''
    多通道输入数据进行卷积运算
    :param X: 多通道输入数据
    :param K: 卷积核
    :return: 单通道输出数据
    '''
    #遍历X和K的第0个维度，进行简单的二维数据的互相关运算，再对通道求和
    return sum(corr2d(x,k) for x,k in zip(X,K))

#计算验证
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
print('多通道输入和卷积运算的结果：',corr2d_multi_in(X, K))

def corr2d_multi_in_out(X,K):
    '''
    对多通道输入的数据进行卷积运算
    :param X: 多通道输入数据
    :param K: 卷积核
    :return: 多通道输出数据
    '''
    #迭代卷积核的第0个维度，美的对多通道输入X执行互相关运算
    #然后将每次的结果堆叠在一起
    return torch.stack([corr2d_multi_in(X,k) for k in K],0)

#计算验证
K = torch.stack((K, K + 1, K + 2), 0)#狗仔多维卷积核
print('多输入多输出的卷积运算后：',corr2d_multi_in_out(X, K))

def corr2d_multi_in_out_1x1(X,K):
    '''
    对于多输入多输出的1x1卷积运算
    :param X: 输入数据
    :param K: 卷积核
    :return: 1x1卷积运算后的结果
    '''
    c_i,h,w = X.shape
    c_o = K.shape[0]
    #因为是关于通道的全连接层，所以将同一个通道内的数据拉伸成一维向量
    #更加形似全连接层的设定
    X = X.reshape((c_i,h*w))
    K = K.reshape((c_o,c_i))
    #进行全连接层中的矩阵乘法运算
    Y = torch.matmul(K,X)
    return Y.reshape((c_o,h,w))

#计算验证——1x1卷积相当于先前实现的多通道输出输入的卷积函数
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6
print('Y1和Y2是同一个对象：',Y1 is Y2)#False

---

汇聚层/池化层

Tips

①池化层的输入和输出通道数保持相同，可以对其padding和stride的数值进行指定；

②池化层的特点——

• 若随着网络的逐层加深，隐藏表示的空间分辨率也逐渐减少，信息得到聚集，则每个神经元相应的感受野也会随之增加；
• 但是最后的输出往往是针对输入数据的全局表示，因此最后一层神经元应该是对全局的一个映射，通过信息的逐渐聚合，就可以生成越来越泛化粗糙的映射，最终实现全局表示学习的功能，并且将卷积层的优势在中间隐层进行保留；
• 池化层是确定性计算，不包含可学习的参数；
• 总而言之，其一可以降低卷积层对位置的敏感性；其二可以降低对空间降采样表示的敏感性

③运算细节
√池化层的形状也不一定是方阵，其相应的stride也可以不等；
√使用池化层处理多通道输入数据时，池化层在每个输入通道上单独进行运算

Codes&Homework

T1&2:将最大池化和平均池化使用卷积运算的形式来实现——
平均池化就是设计一个求均值的卷积核，每个对应位置上的权重都为1，然后将1/num作为整体的系数；
最大池化就是先对输入数据求取argmax，在对应位置上的卷积核设置为1，其余设置为0；

T4:有关不同池化层的比较和思考
Ref:
CSDN-平均池化和最大池化的区别
CSDN-四种池化的区别简介
①均值池化可以减少特征提取过程中因为邻域大小受限造成的估计值方差较大的问题，因此其运算结果可以更多地保留图像的背景信息；
②最大池化能够减少特征提取过程中因为卷积层参数的误差造成的估计均值的偏移，其运算结果可以更多地保留纹理信息；
③随机池化则是按照元素的大小赋予每个元素被选择的概率，再基于概率值对元素进行随机选择；它在平均意义上和均值池化类似，在局部意义上又保留了最大池化的特点；
④全局平均池化用于替代分类器网络中的全连接层，在能够将输出归纳成与分类类别数目相同的向量的同时，大幅度减少网络参数（也即有效防止过拟合现象），并且还赋予了feature map每个通道类别的意义。

T5：最小池化层的作用和意义
Ref：
知乎-池化为什么使用平均或者最大，而不是用最小池化
blog-最小池化有没有意义
如果对于中心对称的激活函数（如d、sigmoid,tanh,linear等），最大池化和最小池化的解空间是一致的——将图像反色（或者将首尾卷积层的权值全都取负值）,可以得到max(x)↔min(-x)；
但是当激活函数并非完全对称时，最小池化就可能会使得网络训练出现过拟合或者梯度消失的情况。

T6:softmax计算与池化
Ref：SoftPool_基于Softmax加权的池化操作|2021新文
上面链接中的文章提出的SoftPool,就是基于softmax加强进行特征图的池化操作，它能够在保持计算和内存高效的情况下，保留特征图的重要信息；且该中池化可以很好地参照区域内的激活值分布，服从一定的概率分布。

import torch
from torch import nn
def pool2d(x,pool_size,mode = 'max'):
    p_h,p_w = pool_size
    y = torch.zeros((x.shape[0]-p_h+1,x.shape[1]-p_w+1))
    for i in range(y.shape[0]):
        for j in range(y.shape[1]):
            if mode == 'max':
                y[i,j] = x[i:i+p_h,j:j+p_w].max()
            elif mode == 'avg':
                y[i,j] = x[i:i+p_h,j:j+p_w].mean()
    return y

#计算验证
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
print('最大池化层计算后：',pool2d(X, (2, 2)))

#可以通过设置stride和padding改变池化层的输出形状
#首先构造一个四维输入张量,样本数和通道数为1
x = torch.arange(16,dtype=torch.float32).reshape((1,1,4,4))
print('输入张量为:',x)
pool2d = nn.MaxPool2d(3)#使用库中的api构建一个3x3的最大池化层
print('3x3最大池化运算后:',pool2d(x))

pool2d_new = nn.MaxPool2d(3,padding = 1,stride = 2)
print('3x3的步长为2的最大池化，对原始数据进行1像素的padding：',pool2d_new(x))

#池化层处理多通道输入数据
x = torch.cat((x,x+1),1)
#在通道维度上连结张量x和x+1，构建两个通道的输入
print('池化运算之前的数据：',x)
pool2d = nn.MaxPool2d(3,padding=1,stride=2)
print('池化运算之后的数据：',pool2d(x))