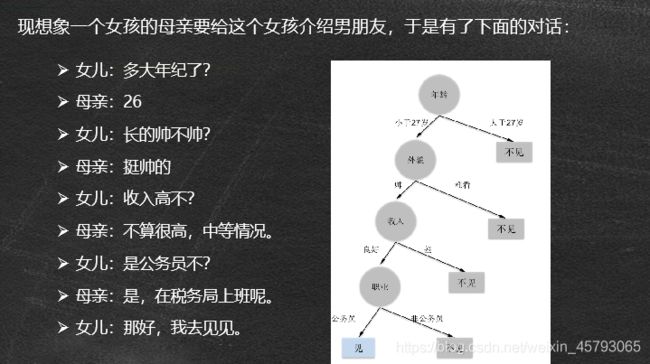
机器学习之决策树与泰坦尼克号生还者案例

决策树

• 决策树是一种简单高效并且具有强解释性的模型，广泛应用于数据分析领域。其本质是一颗自上而下的由多个判断节点组成的树
  

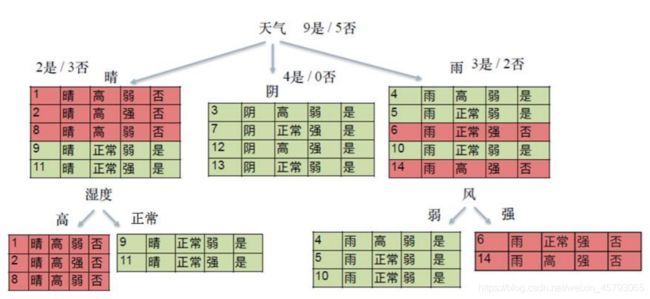
决策树示例

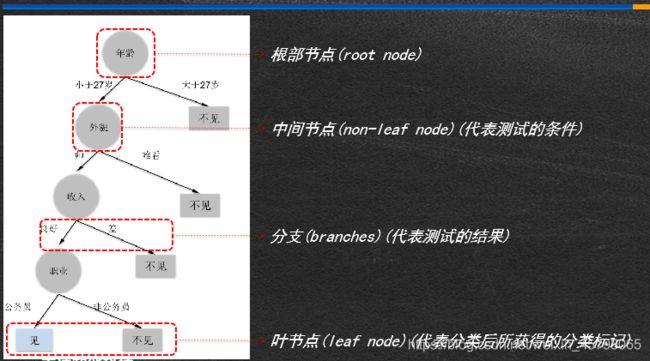
决策树与if-then规则

● 决策树可以看作一-个if-then规则的集合
●由决策树的根节点到叶节点的每一条路径，构建一条规则:路径.上内部节点的特征对应着规则的条件(condition) ，叶节点对应规则的结论
●决策树的if-then规则集合有一个重要性质:互斥并且完备。这就是说，每个实例都被一条规则(一 条路径)所覆盖，并且只被这一条规则覆盖
if (condition)
then
else 决策树中的Condition是什么?
then Condition的确定过程就是特征选择的过程

决策树的目标.

●决策树学习的本质，是从训练数据集中归纳出一-组if-then 分类规则
●与训练集不相矛盾的决策树，可能有很多个，也可能- 一个也没有;所以我们需要选择一个与训练数据集矛盾较小的决策树
●另一角度，我们可以把决策树看成- -个条件概率模型，我们的目标是将实例分配到条件概率更大的那一-类中去
●从所有可能的情况中选择最优决策树，是一个NP完全问题，所以我们通常采用启发式算法求解决策树，得到一-个次最优解
●采用的算法通常是递归地进行以下过程:选择最优特征，并根据该特征对训练数据进行分割，使得各个子数据集都有一个最好的分类

特征选择

●特征选择就是决定用哪个特征来划分特征空间

随机变量

●随机变量(random variable)的本质是一个函数，是从样本空间的子集到实数的映射，将事件转换成一-个数值

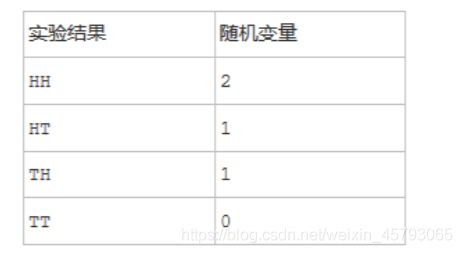
●根据样本空间中的元素不同(即不同的实验结果)，随机变量的值也将随机产生。可以说，随机变量是“数值化”的实验结果
●在现实生活中，实验结果是描述性的词汇，比如“硬币的正面” 、“反面。在数学家眼里，这些文字化的叙述太过繁琐，所以拿数字来代表它们

熵

●熵(entropy) 用来衡量随机变量的不确定性
●变量的不确定性越大，熵也就越大
设X是一-个取有限个值的离散随机变量，其概率分布为:

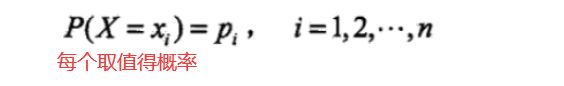
则随机变量X的熵定义为:

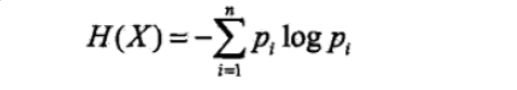
通常，上式中的对数 以2为底或者以e为底(自然对数)，这时熵的单位分别
称为比特(bit) 或纳特(nat)

简单例子：
当随机变量只取两个值，例如1,0时，则X的分布为:
P(X=1)=p, P(X=0)=1-p， 0≤p≤1
熵为:

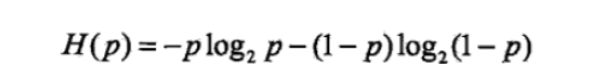
这时，熵H§随概率p变化的曲线如下图所示(单位为比特) :

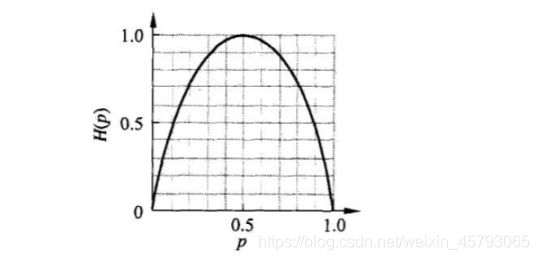
p=1,0 是必然事件，随机事件是零，熵是零
p=0.5 是随机事件 ，熵最大

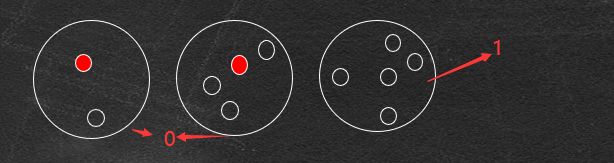
●给三个球分类
→显然一眼就可以看出把红球独自一组，黑球- -组;
-→那么从熵的观点来看，是什么情况呢?

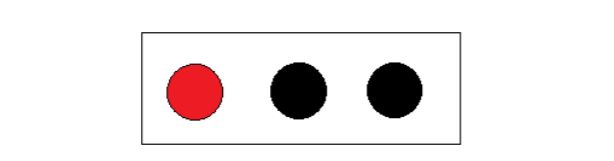
初始状态的熵:
E(三个球)=- 1/3* log(1/3)-2/3 *log(2/3)=0.918

●第一种分类方法是一个红球、一个黑球- -组， 另一个黑球自己一组。
-→在红黑-组中有红球和黑球，红黑球各自出现的概率是1/2.
→在另- -组100%出现黑球，红球的概率是0

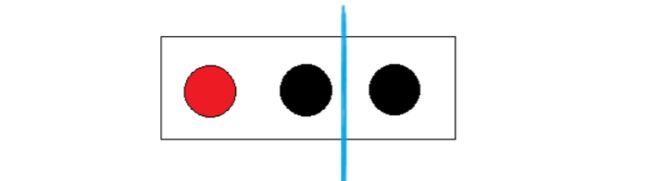
E(红黑|黑)=E(红黑)+E(黑)=-1/2 * log(1/2)-1/2*log(1/2)-1 *log(1)=1
可以看到，分类之后熵反而增大了

●第二种分法就是红球自己- -组，剩下两个黑球- -组
→在红球组中出现黑球的概率是0,在黑球组中出现红球的概率是0,这样的
分类已经“纯”了，也就是分类后子集中的随机变量已经变成确定性的了

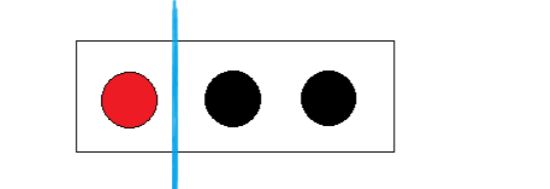
E(红|黑黑)=E(红)+E(黑黑)=-1log(1)-1 log(1)=0

决策树的目标：让熵越来越少
●我们使用决策树模型的最终目的是利用决策树模型进行分类预测，预测我们给出的一-组数据最终属于哪一种类别，这是一一个***由不确定到确定的过程***
●最终理想的分类是，每一-组数据，都能确定性地按照决策树分支找到对应的类别
●所以我们就选择使数据信息熵下降最快的特征作为分类节点，使得决策树尽快地趋于确定

条件熵( conditional entropy )

条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性:

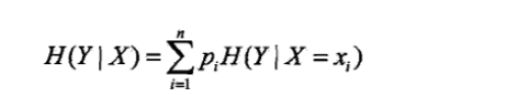
其中，p:=P(X=x)
●熵H(D)表示对数据集D进行分类的不确定性。
●条件熵H(D|A)指在给定特征A的条件下数据集分类的不确定性
●当熵和条件熵的概率由数据估计得到时，所对应的熵与条件熵分别称为经验熵(empirical entropy)和经验条件熵(empirical conditional entropy)

信息增益.

●特征A对训练数据集D的信息增益g(D, A),定义为集合D的经验熵H(D)与特征A给定条件下D的条件熵H(D|A)之差，即
g(D,A)= H(D)- H(D|4)
●决策树学习应用信息增益准则选择特征
●经验熵H(D)表示对数据集D进行分类的不确定性。而经验条件熵H(D|A)表示在特征A给定的条件下对数据集D进行分类的不确定性。那么它们的差，即信息增益，就表示由于特征A而使得对数据集D的分类的不确定性减少的程度
●对于数据集D而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益
●信息增益大的特征具有更强的分类能力

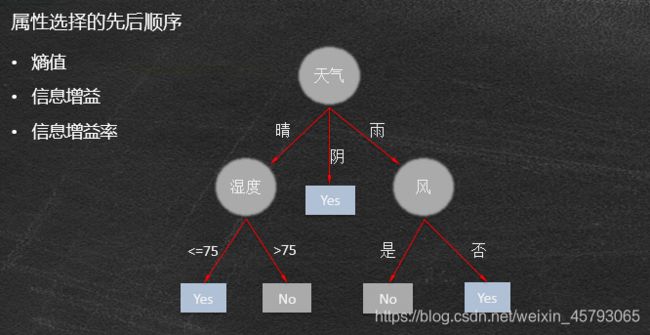
决策树的生成算法

●ID3
-决策树(ID3) 的训练过程就是找到信息增益最大的特征，然后按照此特征进行分
类，然后再找到各类型子集中信息增益最大的特征，然后按照此特征进行分类,
最终得到符合要求的模型。
●C4.5

• C4.5算法在ID3基础上做了改进，用信息增益比来选择特征
  ●分类与回归树(CART)
  由特征选择、树的生成和剪枝三部分组成，既可以用于分类也可以用于回归

决策树泰迪云

打球例子

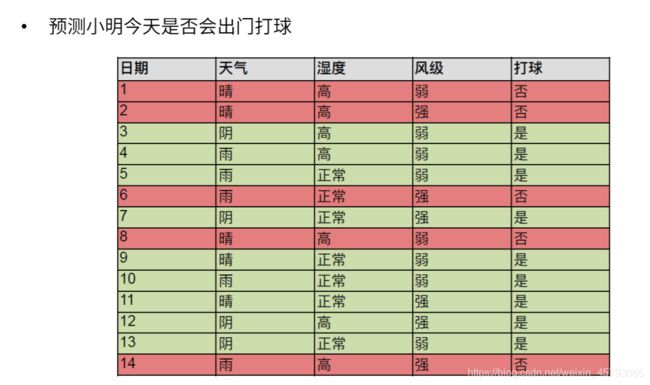
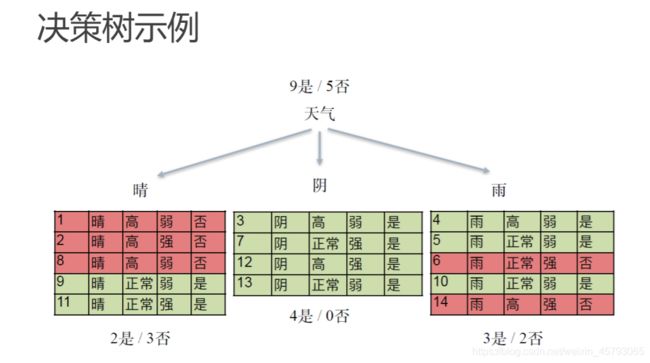
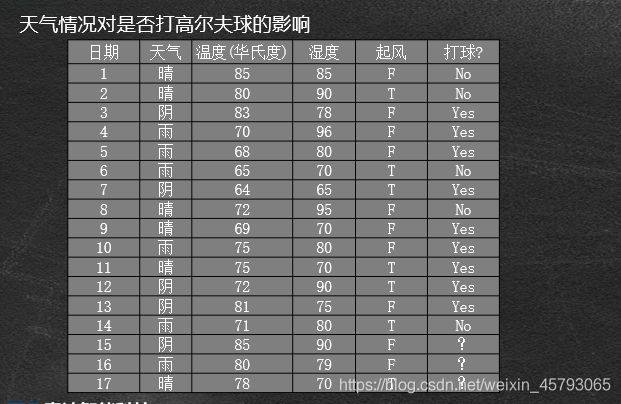
决策树拆分属性选择

问题:对于给定样本集，如何判断应该在哪个属性上进行拆分
●每次拆分都存在多种可能，哪个才是较好的选择呢?
●理想情况:在拆分过程中，当叶节点只拥有单一类别时， 将不必继续拆分。
●目标是寻找较小的树，希望递归过程尽早停止
●较小的树意味着什么?
●当前最好的拆分属性产生的拆分中目标类的分布应该尽可能地单一(单纯)，多数类占优。
如果能测量每个节点的纯度， 就可以选择能产生最纯子节点的那个属性进行拆分:
●决策树算法通常按照纯度的增加来选择拆分属性。

纯度的概念
纯度度量
当样本中没有两项属于同一类:0
当样本中所有项都属于同一类:1
最佳拆分可以转化为选择拆分属性使纯度度量最大化的优化问题
●拆分增加了纯度，但如何将这种增加量化呢，或者如何与其他拆分进行比较呢?
●用于评价拆分分类目标变量的纯度度量包括
●基尼(Gini,总体发散性) CART
.●熵(entropy, 信息量)
●信息增益(Gain) ID3
●信息增益率C4.5, C5.0
●改变拆分准则(splitting criteria)导致树的外观互不相同

熵(entropy)
信息论中的熵:是信息的度量单位，是种对属性"不确定性的度量
属性的不确定性越大，把它搞清楚所需要的信息量也就越大，熵也就越大。必然事件熵值是零
如果一个数据集D有N个类别， 则该数据集的熵为:

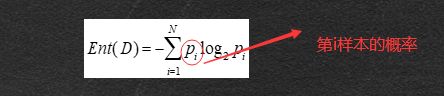
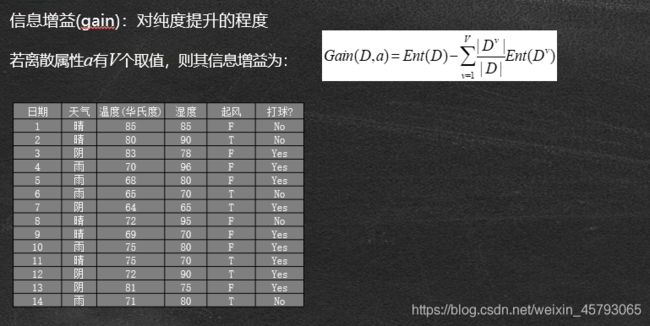
**信息增益(gain)*对纯度提升的程度
若离散属性a有V个取值，则其信息增益为:

决策树算法家族

ID3算法实现

ID3算法的详细实现步骤如下:
a、对当前样本集合，计算所有 属性的信息增益;

b.、选择信息增益最大的属性作为拆分属性，把拆分属性取值相
同的样本划为同一个子样本集;
c、.若子样本集的类别属性只含有单个属性，则分支为叶子节点，
判断其属性值并标上相应的符号之后返回调用处;否则对子
样本集递归调用本算法。

ID3算法是决策树系列中的经典算法之一， 它包含了决策树作为机器学习算法的主要思想，缺点是:
●由于ID3决策树算法采用信息增益作为选择拆分属性的标准，
会偏向于选择取值较多的，即所谓高度分支属性，而这类属性并不一定是最优的属性。
●ID3算法只能处理离散属性，对于连续型的属性，在分类前需要对其进行离散化。

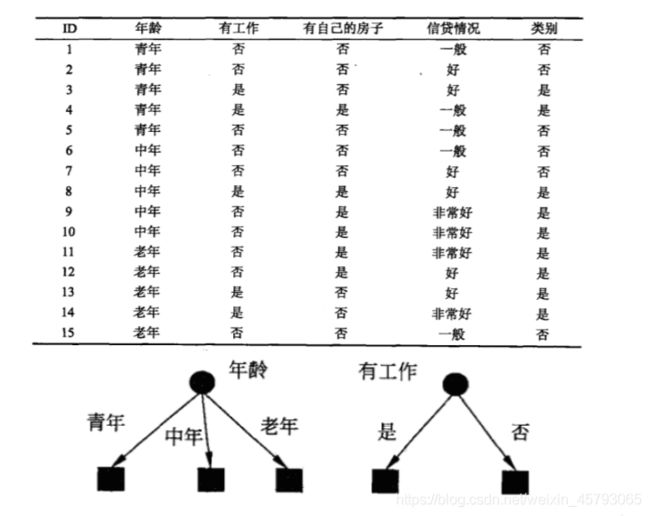
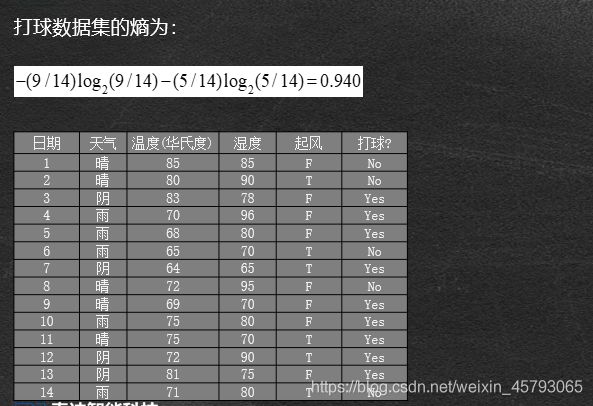
案例：泰坦尼克号生还者

分类——实现类是DecisionTreeClassifier，能够执行数据集的多类分类

●输入参数为两个数组X[n_samples,n_features]和 y[n_samples],X 为训练数据，y 为训练数据的标记数据

●DecisionTreeClassifier 构造方法为：

● sklearn.tree.DecisionTreeClassifier(criterion='gini' , splitter='best' , max_depth=None 

 , min_samples_split=2 

 , min_samples_leaf=1 

 , max_features=None 

 , random_state=None 

 , min_density=None 

 , compute_importances=None 

 , max_leaf_nodes=None) 

●回归——实现类是DecisionTreeRegressor，输入为X，y 同上，y 为浮点数

●DecisionTreeRegressor 构造方法为：

● sklearn.tree.DecisionTreeRegressor(criterion='mse' , splitter='best' , max_depth=None 

 , min_samples_split=2 

 , min_samples_leaf=1 

 , max_features=None 

 , random_state=None 

 , min_density=None 

 , compute_importances=None

 , max_leaf_nodes=None) 

数据：titanic_data.csv
完整代码

import pandas as pd
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.metrics import classification_report #分类报告
import graphviz

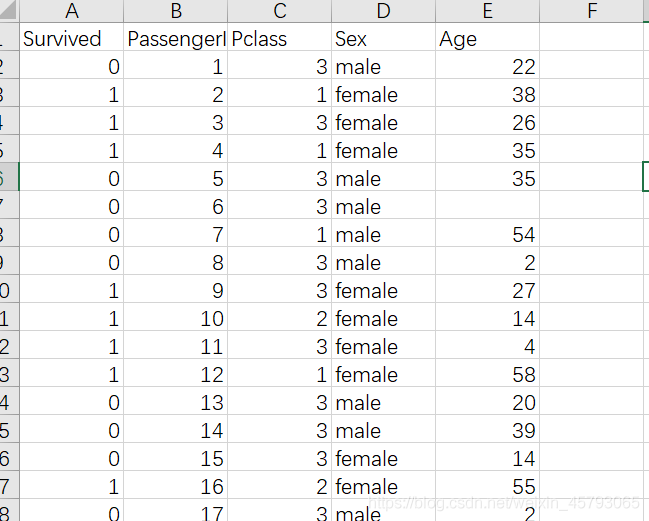
data = pd.read_csv('titanic_data.csv') #导入数据
data

Survived	PassengerId	Pclass	Sex	Age
0	0	1	3	male	22.0
1	1	2	1	female	38.0
2	1	3	3	female	26.0
3	1	4	1	female	35.0
4	0	5	3	male	35.0
...	...	...	...	...	...
886	0	887	2	male	27.0
887	1	888	1	female	19.0
888	0	889	3	female	NaN
889	1	890	1	male	26.0
890	0	891	3	male	32.0
891 rows × 5 columns

fillna()函数详解
inplace参数的取值：True、False
True：直接修改原对象
False：创建一个副本，修改副本，原对象不变（缺省默认）
method参数的取值 ： {‘pad’, ‘ffill’,‘backfill’, ‘bfill’, None}, default None
pad/ffill：用前一个非缺失值去填充该缺失值
backfill/bfill：用下一个非缺失值填充该缺失值
None：指定一个值去替换缺失值（缺省默认这种方式）
limit参数：限制填充个数
axis参数：修改填充方向

 loc函数：主要通过行标签索引行数据  
 iloc函数：通过行号来取行数据（如取第二行的数据）

sklearn.tree.DecisionTreeClassifier更多了解

import pandas as pd
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.metrics import classification_report #混淆矩阵分类报告
import graphviz

data = pd.read_csv('titanic_data.csv') #导入数据

data.drop('PassengerId', axis=1, inplace=True)   # 删除PassengerId 列,axis=1删除列，axis=0删除行，inplace=True对data数据处理(删除PassengerId标签)/false不处理

data.loc[data['Sex'] == 'male', 'Sex'] = 1       # 用数值1来代替male，用0来代替female 
data.loc[data['Sex'] == 'female', 'Sex'] = 0
data.fillna(data['Age'].mean(), inplace=True)    # 数据中有一些是空的，用均值来填充缺失值

Dtc = DecisionTreeClassifier(max_depth=5, random_state=8)    # 构建决策树模型，max_depth数最大深度
Dtc.fit(data.iloc[:, 1:], data['Survived'])       # 模型训练  传入x,y得到函数 ,data.iloc[:, 1:]所有行后三列数据
pre = Dtc.predict(data.iloc[:, 1:])               # 模型预测   传入测试x,得到预测y
pre == data['Survived']                           # 比较模型预测值与样本实际值是否一致
classification_report(data['Survived'], pre)      # 分类报告

结果：

            precision    recall  f1-score   support\n\n           0       0.84      0.88      0.86       549\n           1       0.79      0.73      0.76       342\n\n    accuracy                           0.82       891\n   macro avg       0.82      0.81      0.81       891\nweighted avg       0.82      0.82      0.82       891\n'

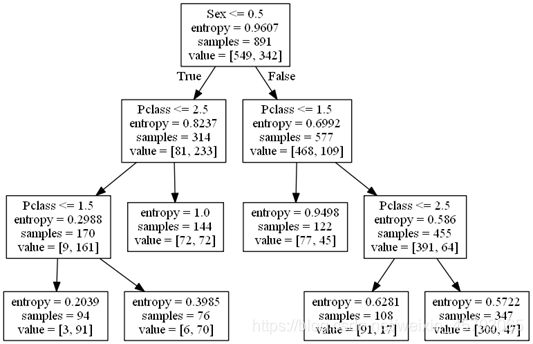
如要将决策树可视化，还需要安装Graphviz（跨平台的、基于命令行的绘图工具），并将安装路径添加至系统变量，生成的效果图如下：
https://graphviz.gitlab.io/_pages/Download/Download_windows.html

import pandas as pd
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.metrics import classification_report #混淆矩阵分类报告
import graphviz

data = pd.read_csv('titanic_data.csv') #导入数据

data.drop('PassengerId', axis=1, inplace=True)   # 删除PassengerId 列,axis=1删除列，axis=0删除行，inplace=True对data数据处理(删除PassengerId标签)/false不处理

data.loc[data['Sex'] == 'male', 'Sex'] = 1       # 用数值1来代替male，用0来代替female 
data.loc[data['Sex'] == 'female', 'Sex'] = 0
data.fillna(data['Age'].mean(), inplace=True)    # 数据中有一些是空的，用均值来填充缺失值

Dtc = DecisionTreeClassifier(max_depth=5, random_state=8)    # 构建决策树模型，max_depth数最大深度
Dtc.fit(data.iloc[:, 1:], data['Survived'])       # 模型训练  传入x,y得到函数 ,data.iloc[:, 1:]所有行后三列数据
pre = Dtc.predict(data.iloc[:, 1:])               # 模型预测   传入测试x,得到预测y
pre == data['Survived']                           # 比较模型预测值与样本实际值是否一致
classification_report(data['Survived'], pre)      # 分类报告

dot_data = export_graphviz(Dtc, feature_names=['Pclass', 'Sex', 'Age'], class_names='Survived')
graph = graphviz.Source(dot_data)       # 决策树可视化
graph