机器学习读书笔记：线性模型

前言

​ 从线性模型开始，就开始涉及到不同的学习算法和模型了。根据预测结果的不同，可以有几种类型的问题：

• 回归问题，也就是预测值为连续值，$y\in R$。
• 分类问题，也就是预测值为离散值，$y\in [C_1,C_2...C_n]$。
• 还有一种是一种特定的分类问题，也就是二分类。$y\in [TRUE,FALSE]$。

​ 我自己对学习的理解就是想学习获得一个属性集合$X$到预测值$y$的一个映射：$f(x),x\in X$。$f(x)$是未知的，机器学习的任务就是通过数据去猜$f(x)$长什么样。但是猜不能瞎猜，得有章法的猜。线性模型就时假设预测值与属性集合之间是一个线性关系。后续的各种模型就是各种不同的猜法。

线性回归

一元线性回归

​ 拿之前的栗子来说，假设火车晚点只与下雨的雨量有关系，而且假设雨量与晚点的时间成线性关系。那么这就是一个典型的一元线性回归问题。这个函数我们在初高中就学过：
$$y=ax+b$$
​ 如果我们确定了等号右侧的参数a和b，每来一个数据属性x，自然就可以计算得到预测值y。

​ 那么怎么得到参数a和b呢。当然是用已知的数据集，假设有数据集$D=\{(x_i,y_i){\}}_{i=1}^m$，也就是说有m个(x, y)这样的数据样本集。我们需要获得一个(a, b)参数，这个参数是的映射$f(x)$在数据集$D$上的输出与标记值的差异最小。那么怎么计算差异呢，直接计算输出值与标记值之间的差值就好：$f(x)-y$，但是因为会对所有的样本差异进行求和，此时会正负抵消，所以我们加个平方，变成：
$$\sum _{i=1}^m(f(x_i)-y_i{)}^2$$
​ 然后因为$f(x)=ax+b$，就把公式变成：
$$\sum _{i=1}^m(y_i-a{x}_i-b{)}^2$$
​ 然后就是对a和b求偏导(各种公式变换，有兴趣的可以去看一下，编辑公式太费劲)，就可以得到a和b的取值了。

让这样一个数据偏差的乘方最小的方法就叫做**“最小二乘法”**。
$$a=\frac{{\sum }_{i=1}^m{y}_i(x_i-\overline{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}$$

$$b=\frac{1}{m}\sum _{i=1}^m(y_i-a{x}_i)$$

​ 我们用点数据来试一下。

一元线性回归python代码

关于雨量和晚点的问题，假设我们有10个样本：

(50, 3)

(45, 2.4)

(70, 4)

(75, 4.2)

(80, 4.1)

(30, 2)

(90, 7)

(80, 4.3)

(65, 3.5)

(70, 4.3)

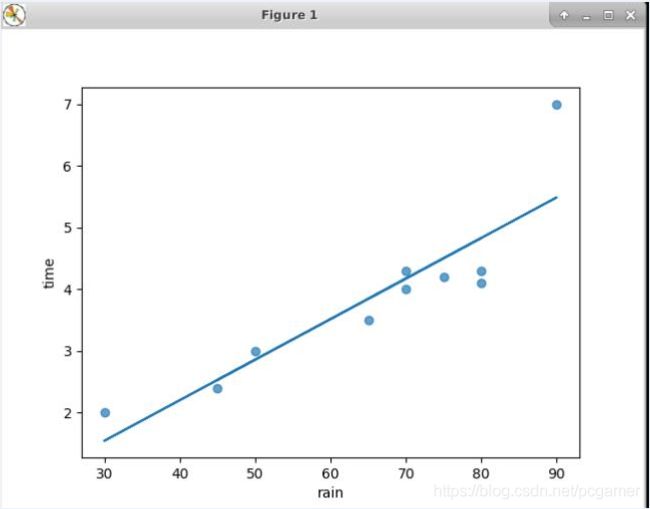
将点画到坐标系中，再通过计算得到a和b(下面有python代码)，然后画一根$y=ax+b$的直线：

​ 可以看出，基本上还是贴着这些点过去的。

附代码如下：

import numpy as np;
import matplotlib.pyplot as plt;

x = [50,45,70,75,80,30,90,80,65,70];
y = [3,2.4,4,4.2,4.1,2,7,4.3,3.5,4.3];


plt.scatter(x,y,alpha=0.7)
plt.xlabel('rain');
plt.ylabel('time');


avarage_x = np.sum(x)/len(x);
a = np.sum(np.multiply(y,(x-avarage_x)));
b = np.sum(np.multiply(x,x));
c = np.sum(x)*np.sum(x)/len(x);

w = a/(b-c);
print(w);

b = np.sum(np.subtract(y,np.multiply(w,x)))/len(x);
print(b);

y_= np.multiply(w,x)+b;

plt.plot(x,y_);
plt.show();

多元线性回归

​ 假设上面的a不止一个属性，比如上面的问题变成火车晚点由“雨量”、“乘车人数”、“风级”等一堆七七八八的原因导致，那么我们就需要获得这些属性的值。我们可以把$a$从一个标量变成矢量$a^T$。
$$f(x_i)=a^T{x}_i+b$$
​ 更进一步的，把常量$b$也弄到向量里：令$\hat{a}=(a^T;b)$。

​ 和一元线性回归类似，我们也是使用最小二乘法去获得参数向量$\hat{a}$。

​ 把m个样本的d个属性组成一个矩阵$X$，因为属性向量$\hat{a}$将常量$b$放进去了，为了满足矩阵乘法运算，所以将矩阵$X$的最后一列置为1：
$$X=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& ...& x_{1d}& 1\\ x_{21}& x_{12}& ...& x_{1d}& 1\\ ...& ...& ...& ...& 1\\ x_{m1}& x_{m2}& ...& x_{mn}& 1\end{array}\right]$$
​ “最小二乘法”的矩阵式为，求得一个向量$\hat{a}$，使得：
$$\hat{a}=min(y-Xa{)}^T(y-Xa)$$
​ 这里所有的乘法、减法都是矩阵计算，第一个括号里的$(y-Xa{)}^T$是对计算后的矩阵$(y-Xa)$进行转置操作。转置之后恰好可以与原矩阵$(y-Xa)$相乘，达到了和标量类似的$(y-f(x){)}^2$的效果。

​ 同样，对上面的公式进行求导并使求导后的式子等于0得到：
$$\begin{gathered} 2X^T(Xa-y)=0 \\ {X}^{T}Xa=X^{T}y \\ a=(X^{T}X{)}^{-1}{X}^{T}y \end{gathered}$$
​ 公式里的$(X^{T}X{)}^{-1}$是X的转置乘以X之后矩阵的逆矩阵。

​ 在很多情况下，矩阵$(X^{T}X)$是不可逆的。这里我讲下我理解的工程：

• 矩阵$X$是一个$m\ast d$的矩阵，m为样本数(行数)；d为属性数(列数)；那么转置矩阵$X^T$就是一个$d\ast m$的矩阵。$X^{T}X$就是一个$d\ast d$的矩阵。
• 在很多情况下，样本的属性数是远大园样本数的，也就是$d>m$。这就是在矩阵$(X^{T}X)$中有很多为0的整行，这样的矩阵是不可逆的。具体是啥原因，大家可以去翻一下矩阵相关的数学书，和矩阵的秩啊、行列式啊等七七八八的概念有关。

​ 不可逆的话也不是说没办法，只是说无法求得准确的解析解。

1. 如果选择偏好的话，也就是选择其中某些属性集$d\prime$，就可以组成一个可逆的矩阵进行计算，因为这样的$d\prime$集合有多个，所以就要选择偏好，比如那些重要的参数组成这个属性集。常见的做法是引入正则化
2. 使用梯度下降法进行求解。

多元线性回归python代码

​ 假设上面就是加入了乘车人数这一个属性，同样的搞10个样本出来：

(雨量，乘车人数，晚点时间)

(50, 100, 3)

(45, 80, 2.4)

(70, 120, 4)

(75, 140, 4.2)

(80, 120, 4.1)

(30, 80, 2)

(90, 140, 7)

(80, 100, 4.3)

(65, 90, 3.5)

(70, 95, 4.3)

通过$(X^{T}X{)}^{-1}{X}^{T}y$来计算得到$a$值。

参考代码：

import numpy as np;
import matplotlib.pyplot as plt;

x_1 = [50,45,70,75,80,30,90,80,65,70];
x_2 = [100,80,120,140,120,80,140,100,90,95];
b = [1,1,1,1,1,1,1,1,1,1];
y = [3,2.4,4,4.2,4.1,2,7,4.3,3.5,4.3];

X=[];
X.append(x_1);
X.append(x_2);
X.append(b);

Y=[]
Y.append(y);

X_T=np.matrix(X);
X_=np.matrix(np.transpose(X));
Y_=np.matrix(np.transpose(Y));


A = X_T*X_;

tt= A.I*X_T;
w = A.I*X_T*Y_

print(w)

print('new value coming: x=(100, 130)');
x1_new = 100;
x2_new = 130;

x_new = [100, 130, 1];

NEW = [];
NEW.append(x_new);

NEW_ = np.matrix(NEW);
y_new = NEW_*w

print('the new value is: ')
print(y_new);

计算得到的a值：

[[ 0.05277084]
[ 0.01405861]
[-1.07373189]]

结果：

new value coming: x=(100, 130)
the new value is:
[[6.03097126]]

预测在雨量100，乘车人数130的情况下，会晚点6分钟。

二分类问题

对数机率回归

​ 书上给出了一个广义线性模型的概念，也就是说在上面提到的线性模型$(a^{T}x+b)$的基础上，可以再叠加一个单调可微函数$g(x)$，同样是满足线性关系。

​ 然后再引入一个函数Sigmold函数：
$$g(x)=\frac{1}{1+e^{-z}}$$
​ 那么x，y的映射关系就变成了：
$$y=\frac{1}{1+e^{-(a^T+b)}}$$

​ 将这个公式两边再变化一下：
$$ln\frac{y}{1-y}=a^T+b$$
​ 通过这个公式就可以看出，$\frac{y}{1-y}$中，可以将y视作样本x为正例的比例，那么1-y就正好是样本x为反例的比例。两者一比基本上就可以看做是正例与反例的比例，也可以看做是正例的机率。再取个对数操作，所以叫做对数机率回归。

​ 如果是满足对数机率回归的$(x^T,y)$的分类问题，需要使用梯度下降的方法来求解a和b。那个后续再说吧。

LDA-线性判别分析

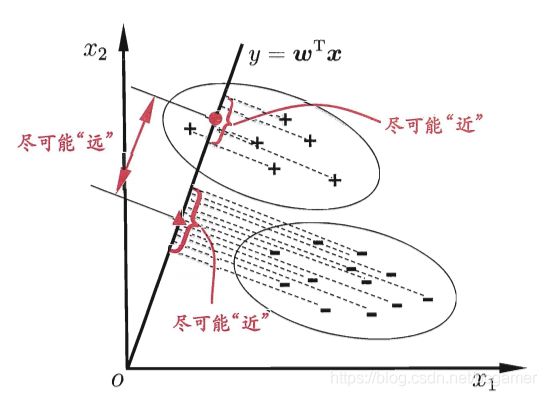
​ LDA的思想是，计算每个正例和反例点到某条直线(二维)，或者平面(三维)上的投影，多维的情况也是投影计算。通过各种计算方法得到一个$\omega$，是的正例之间的投影距离和最小，而反例和正例之间的投影距离最大。

​ 至于后面那一串公式，实在看不懂。后续再说吧。

多分类问题

​ 多分类问题，可以看成是多个二分类问题的组合。那么对于问题的拆分组合，有三种方式：

1对1 O(One) v O(One)

​ 假设总体样本总共有N类，那么对N个样本分类进行一一配对，总共会有$N(N-1)/2$中配对，每一个配对就是一个二分类问题。假设分类$C_i$和$C_j$在一个配对中，可以假设$C_i$为正例，$C_j$为反例进行二分类训练。把同一个样本放到所有的$N(N-1)/2$个分类器中去，每一个样本就有$N(N-1)/2$个输出结果。此时就可以做一个决策问题了，比如最简单的，那种分类占比大就选哪个。

一对其他 O(One) v R(Rest)

​ 假设总体样本总共有N类，首先挑出一个分类$C_i$，将此类别作为正例，其他的都作为反例进行训练和输出。可以总共准备N个这样的分类算法，每次都选择一个$C_i$作为正例，其他作为反例进行训练和测试。样本进入每个这个N个学习算法进行输出，同样需要做一个决策问题，可以选占比最大的那个,或者是置信度最高的那一个等等。

​ 和OvO方式相比：OvR只需要训练N个算法就可以了，而OvO需要训练$N(N-1)/2$个算法。明显是OvR比较划算。但是OvO每个算法的训练样本量是要低于OvR的，因为OvR的每个算法训练都需要将所有的样本进行训练，而OvO只需要将配对的相应类别($C_i,C_j$)的样本进行训练即可。所以，如果类别比较多的话，OvO的计算量也许还会小一点。

多对多 M(Many) v M & ECOC

​ 多对多的话就没那么极端，选出若干个类别来作为正例，剩下的若干类别就成为反例。那么就有两个问题：

1. 怎么分？
2. 训练完了怎么决策？

​ 直接来看一个比较常用的策略：ECOC（纠错输出码：Error Correcting Output Codes）。

​ 这个书上文字描述的挺绕，举个栗子简单一点，假设我们有一个5分类的问题，

1. 第一步就是把这些类别进行划分，N个类别进行M次划分，分别作为正例和反例，在ECOC方法中就叫做编码。

   假设我们令M=4：

   M1：{1， 3}为正例，{2，4，5}为反例。训练出来的算法为$f_1(x)$。那么$f_1(x)$对5个类别的编码情况如下(1表示正例，-1表示反例)：

   1, -1, 1, -1, -1

   M2：{2， 5}为正例，{1，3，4}为反例。训练出来的算法为$f_2(x)$。那么$f_2(x)$对5个类别的编码情况如下(1表示正例，-1表示反例)：

   -1, 1, -1, -1, 1

   M3：{2， 3， 5}为正例，{1，4}为反例。训练出来的算法为$f_3(x)$。那么$f_3(x)$对5个类别的编码情况如下(1表示正例，-1表示反例)：

   -1, 1, 1, -1, 1

   M4：{3， 5}为正例，{1，2，4}为反例。训练出来的算法为$f_4(x)$。那么$f_4(x)$对5个类别的编码情况如下(1表示正例，-1表示反例)：

   -1, -1, 1, -1, 1

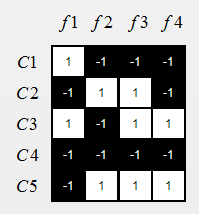
   建立一个和书上类似的矩阵，这就完成了编码：

2. 把测试样本丢到算法中去进行预测(解码)：

   总共有2个样本如下：

   ​ (x, y)

   ​ (100, 1)

   ​ (132, 2)

   假设第一个样本的预测值为：$f_1:1,f2:-1，f_3:-1,f_4:-1$，那么，拿这个编码去上面的矩阵中匹配行，明显能匹配上C1行，那么这个样本的预测值就是1。

   什么情况下纠错呢，假设第二个样本的预测值为：$f_1:-1,f2:1，f_3:-1,f_4:-1$。此时，算法$f_3$对样本判断失误。所以这个编码与上述编码矩阵中的每一行都匹配不上，此时，就需要求这个编码与每一行的距离了。以海明距离为例：此错误编码与C1的海明距离为2，与C2的海明距离为1，C3为4，C4为1，C5为4。此时，可能会被判断为C2类或者C5类。

   这个时候能看出，如果某个算法发生错误，实际上是可以通过编码的距离来进行纠错的。

   但是为啥我们这还是出了两个类别呢，这是因为我们的M不够多，对于有限类别，M的越多，纠错能力就越强，比如M=7。那么每个编码的码长就越长，错一个与其他编码的重复概率就会降低，有兴趣的可以去看一看编码相关的内容。

   但是增加编码的代价是要增加算法的个数，也就也为这增加训练的计算量。

类别不平衡

​ 假设训练样本中的正例、反例比例不平均，1000个样本中10个正例，990个反例。那么此时训练出来的算法对正例的判断能力是不够的，但是如果反例多的话，学习算法的准确率还是能达到99%。这样的算法是没有太大用处的。

​ 解决这个问题的策略就是“再缩放”，简单的说就是减少这个比例的差异。

• 对反例进行“欠采样”，就是丢掉一些反例，自然训练集中的正例、反例比例下降了
• 对正例进行“过采样”，在正例里重复引入一些正例样本做为训练集。但是这样可能会破坏样本的一些分布信息。