深蓝学院-视觉SLAM课程-第3讲笔记-李群和李代数
课程Github地址:https://github.com/wrk666/VSLAM-Course/tree/master
0. 内容
1. 什么是群
为什么要引入群?

因为求旋转矩阵或者变换矩阵的导数时,加法不再成立,所以求矩阵的导数需要引入其他的方法,于是就引入了群。

因为加法在整数上面呈交换群,所以2+3=3+2=5
例如:在加法上的运算,幺元为0,a+(-a)=0
在乘法上,幺元为1, a ∗ 1 a = 1 a* \dfrac{1}{a}=1 a∗a1=1

旋转矩阵可逆,是正交的矩阵,与矩阵乘法构成群。
如果不成群的话,基本上就没什么必要去讨论了。
一般的 n × n n\times n n×n的可逆矩阵就是一般线性群GL(n)
2. 李群与李代数
具有连续(光滑)性质的群叫做李群(Lie Group)。
基础知识补充:《微分几何》
流形的定义(我的理解):流形是一个空间。流形是低维数据映射到高维形成的一个空间。高维空间中的数据会产生维度上的冗余,但实际上这些数据只需要使用较低的维度就能够唯一表示。而之前听到过的流形学习就是:假设数据是均匀采样于一个高维的欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维的流形结构,及找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。他是从观测到的现象中寻找事物的本质,已找到产生数据的内在规律。
下列图片来自参考博客
SO(3)和SE(3)只有定义良好的乘法,没有加法,所以难以及逆行取极限,求导等操作。(前面不是说是为了求出旋转矩阵的导数才引入群的吗?这里怎么还不能求呢?)

首先由SO(3)(旋转矩阵)来引入李代数。
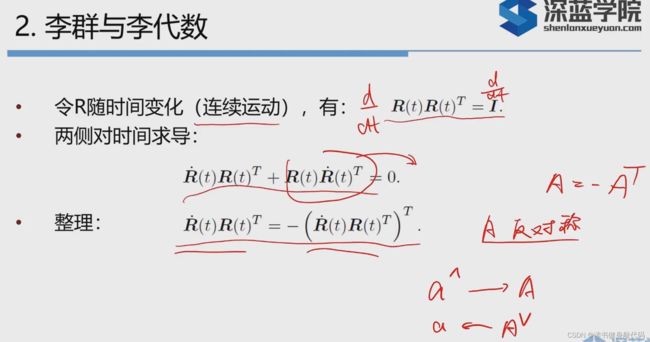
首先对于旋转矩阵,是正交的,两侧对时间求导,整理之后得到一个反对称矩阵
R ˙ ( t ) R ( t ) T \dot{R}(t)R(t)^T R˙(t)R(t)T
a^表示由向量到反对称矩阵,而
![]()
表示由反对称矩阵表示向量。
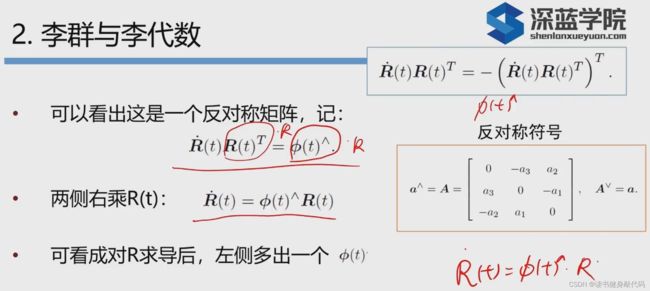
可看作对R(t)求导之后,左侧多出一个 ϕ ( t ) \phi(t) ϕ(t)^

对R(t)进行一阶泰勒展开,在 t 0 t_0 t0附近 ϕ \phi ϕ不变,化为微分方程,带入初始条件解之得(有一些细节没有仔细讲)

任意给定一个向量 ϕ \phi ϕ,能够找到一个对应关系,
e ϕ ^ 0 t = R ( t ) e^{\hat\phi_0 t}=R(t) eϕ^0t=R(t)
其中 ϕ \phi ϕ是李代数,对应关系是指数映射, R R R是李群。
下面是李代数的严格定义:

给出结构带进去验证就能看是否是李代数。

[,]是李括号运算。
SO(3)是矩阵,so(3)是向量(其实矩阵和向量一一对应,都可以,但是这样更自然),李括号是作用在向量上的运算。

SE(3)的李代数是6维向量, ρ \rho ρ表示平移, ϕ \phi ϕ表示旋转,而上尖尖^不再表示对称矩阵,但仍然保留记法。只是把旋转部分的 ϕ \phi ϕ做反对称,而平移部分不变,由(6,1)->(4,4)
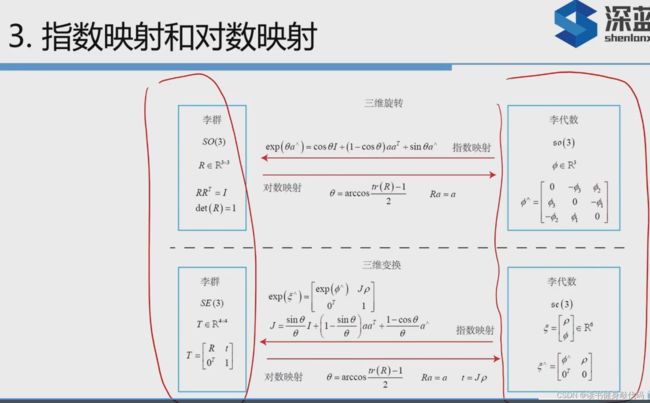
3. 指数映射和对数映射

通过无穷级数展开(见高数18讲P244)
e x = ∑ n = 0 ∞ x n n ! e^x=\sum_{n=0}^\infty \frac{x^n}{n!} ex=n=0∑∞n!xn
sin x = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! \sin x=\sum_{n=0}^\infty (-1)^n\frac{x^{2n+1}}{(2n+1)!} sinx=n=0∑∞(−1)n(2n+1)!x2n+1
cos x = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! \cos x=\sum_{n=0}^\infty (-1)^n\frac{x^{2n}}{(2n)!} cosx=n=0∑∞(−1)n(2n)!x2n
其中3个展开的收敛于均为 − ∞ < x < + ∞ -\infty
加上下面的性质能够处理高次幂
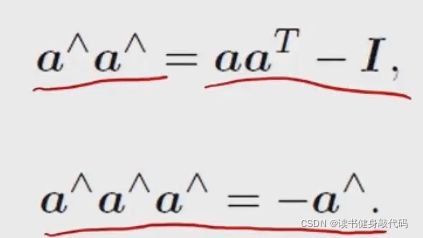
即可推得罗德里格斯公式。

那么说明李代数so(3)的物理意义实际上就是旋转向量(罗德里格斯公式就是旋转向量转旋转矩阵,其左侧就是旋转矩阵 R R R)。反之,给定旋转矩阵就能求得旋转向量,可以使用对数映射或者下面的转换关系:
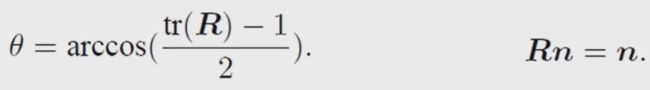
对于SE(3)

其中平移向量 ρ \rho ρ和变换矩阵中的平移量 t t t 差了一个系数矩阵,即为雅可比矩阵,跟角度有关,旋转部分正好是一个so(3)。
本部分小结
4. 求导与扰动模型

还是求导,由于李群无加法,所以要求导得从李代数角度出发,在李代数上加一个小的量 δ ϕ \delta \phi δϕ然后用指数运算变换成李群,但是问题是李代数中的加法是否等价于李群的乘法。在标量时显然成立,a,b是标量时显然成立 e a ∗ e b = e a + b e^a*e^b=e^{a+b} ea∗eb=ea+b,但是当幂是矩阵时不成立。

引入BCH公式:

矩阵两个exp然后取ln展开是一个关于李括号的一个式子,相当复杂,进行一些近似之后:
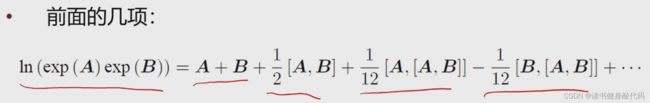
当两个矩阵其中有一个为小量时,顾略高阶做以下近似:

当左乘一个小量时,系数就是左雅可比矩阵;当左右乘一个小量时,系数就是右雅可比矩阵,常用左雅可比。

所以李代数上进行小量加法时,相当于利群上左(右)乘一个带雅可比的量。

SE(3)比SO(3)复杂,右上角的 Q r Q_r Qr很复杂。
- 李代数上加一个小量,求变化率
- 利群上乘一个小量,求相对于李代数的变化率
导数模型:

逆用BCH公式,然后泰勒展开,二次项就为0了,所以泰勒展开就只保留前两项。
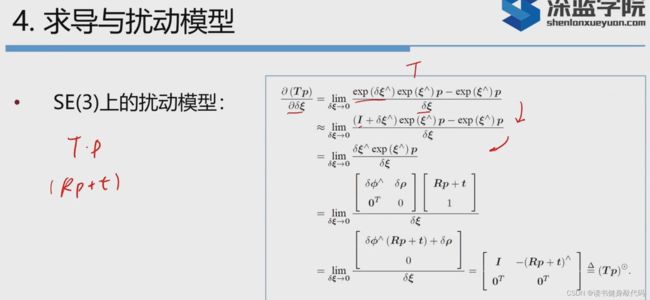
扰动模型,左(右)乘一个扰动对应的群

SE(3)的扰动模型:左乘扰动