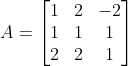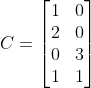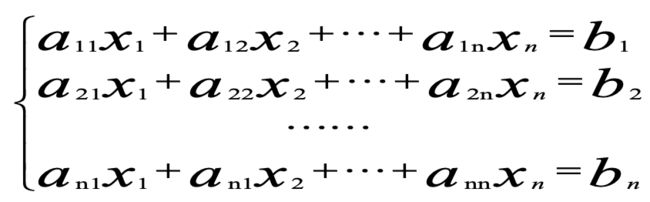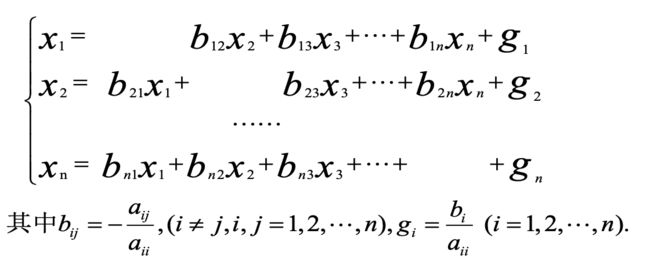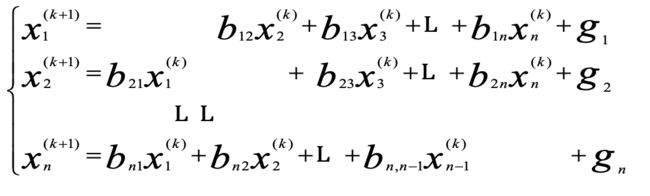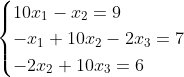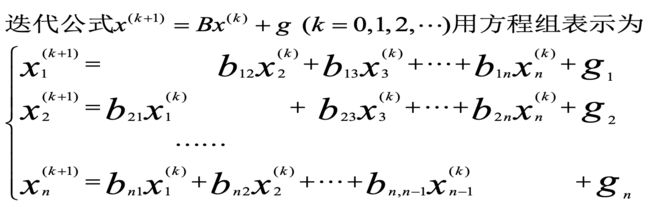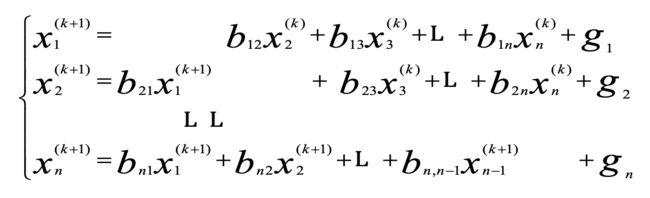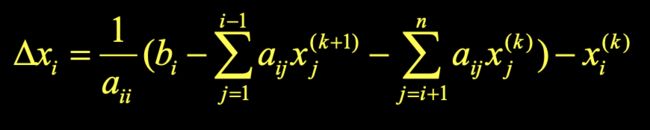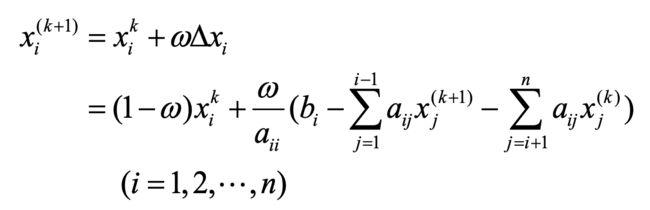基于MATLAB的迭代求解线性方程组（附完整代码与算法）
前言
在之前的文章中更新了线性方程组的基本解法，大型方程组的分解求法。本节将介绍线性方程组的迭代求解。
一. 三个变换
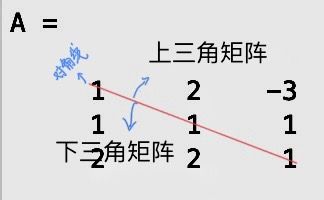
在线性方程组的迭代求解中，会用到系数矩阵A的上三角矩阵、对角矩阵和下三角矩阵。这三种变化在MATLAB中，可以直接利用函数实现。
1.1 上三角变换
triu(A,1)1.2 对角变换
diag(A)1.3 下三角变换
tril(A,-1)针对此类矩阵的解释，可以参看这篇文章：
MATLAB:矩阵基础_唠嗑！的博客-CSDN博客
例题1
对以下矩阵A做此三种变换。
解：
MATLAB代码如下：
clc;clear;
A=[1 2 -3;1 1 1;2 2 1];
%上三角变换
up=triu(A,1)
%对角变换
diag=diag(A)
%下三角变换
down=tril(A,-1)运行结果：
up =
0 2 -3
0 0 1
0 0 0
diag =
1
1
1
down =
0 0 0
1 0 0
2 2 0
分析：
二. Sylvester方程
Sylvester方程的形式如下：
此方程中，A是
矩阵，B是
矩阵，C和X都是
矩阵。
在MATLAB中可以直接调用函数求解，如下：
X=sylvester(A,B,C)例题2
求解Sylvester方程AX+XB=C的解X。其中A,B,C矩阵如下：
，
，
解：
MATLAB代码如下：
clc;clear;
A=[1 0 2 3;4 1 0 2;0 5 5 6;1 7 9 0];
B=[0 -1;1 0];
C=[1 0;2 0;0 3;1 1];
X=sylvester(A,B,C)运行结果如下：
X =
0.4732 -0.3664
-0.4006 0.3531
0.3305 -0.1142
0.0774 0.3560
三. Jacobi迭代法
原方程组Ax=b中的矩阵A可以写成，如下：
上式子中-L和-U分别为A矩阵的严格下，上三角部分，当然不包含对角元素。其中矩阵D的表达如下：
![D=diag[a_{11},a_{22},\cdots,a_{nn}]](http://img.e-com-net.com/image/info8/0858c0b9d9ef4575aee27037dd82cef8.gif){kind=small}
根据迭代的思想，x可得如下表达式：
上式子中的B，f理解如下：
为了更好理解这种迭代形式，将原线性方程组写全，如下：
如果系数矩阵非奇异，即
，那么可得：
运用迭代公式
，最终的方程组如下：
在调用jacobi()函数之前，需要提前编码，我们来看下jacobi函数的内部结构，如下：
function y=jacobi(a,b,x0)
D=diag(diag(a));
U=-triu(a,1);
L=-tril(a,-1);
B=D\(L+U);
f=D\b;
y=B*x0+f;
n=1;
while(norm(y-x0))>=1.0e-6
x0=y;
y=B*x0+f;
n=n+1;
end
n
end例题3
设x0=0，精度为
，利用Jacobi方法求解以下方程组。
解：
MATLAB代码如下：
clc;clear;
a=[10 -1 0;-1 10 -2;0 -2 10];
b=[9;7;6];
jacobi(a,b,[0;0;0]) %注意初始值也为一个矩阵
%对jacobi函数的定义
function y=jacobi(a,b,x0)
D=diag(diag(a));
U=-triu(a,1);
L=-tril(a,-1);
B=D\(L+U);
f=D\b;
y=B*x0+f;
n=1;
while(norm(y-x0))>=1.0e-6
x0=y;
y=B*x0+f;
n=n+1;
end
n
end运行结果：
n =
11
ans =
0.9958
0.9579
0.7916
四. Gauss-Seidel迭代法
借助Jacobi的方法，迭代方程也可以如下形式：
同样地，-L、-U分别为A的严格下、上三角部分，且不包含对角线元素。G，f,D的定义如下：
![G=(D-L)^{-1}U,\;f=(D-L)^{-1}b,\;D=diag[a_{11},a_{22},\cdots,a_{nn}]](http://img.e-com-net.com/image/info8/2e376ca7c9be40719ab59a9d94f8b4dd.gif){kind=small}
为了深入理解此种迭代方式，可列出矩阵中的元素。
在迭代计算过程中，需要同时保留两个近似解向量
和
。由此可以把迭代公式改写为如下：
备注：由于显示的原因，上式子中的“L"代表省略号
由此可以在MATLAB中编码seidel()函数，如下：
function y=seidel(a,b,x0)
D=diag(diag(a));
U=-triu(a,1);
L=-tril(a,-1);
G=(D-L)\U;
f=(D-L)\b;
y=G*x0+f;
n=1;
while norm(y-x0)>=1.0e-6
x0=y;
y=G*x0+f;
n=n+1;
end
n
end
例题4
设x0=0，精度为，利用Gauss-Seidel方法求解以下方程组。
解：
MATLAB代码如下：
clc;clear;
a=[10 -1 0;-1 10 -2;0 -2 10];
b=[9;7;6];
seidel(a,b,[0;0;0])
function y=seidel(a,b,x0)
D=diag(diag(a));
U=-triu(a,1);
L=-tril(a,-1);
G=(D-L)\U;
f=(D-L)\b;
y=G*x0+f;
n=1;
while norm(y-x0)>=1.0e-6
x0=y;
y=G*x0+f;
n=n+1;
end
n
end运行结果：
n =
7
ans =
0.9958
0.9579
0.7916
分析：此例子可以直接求解。也可能会出现使用Seidel迭代时，结果不收敛的情况。
五. SOR迭代法
在某些情况下，Jacobi法和Gauss-Seidel法收敛的过程较慢，为了进一步改进，可以引入一种新的迭代法：逐次超松弛迭代法（Succesise Over Relaxation)，简记为SQR法。
迭代的公式如下：
上式子中，w的最佳值一般在[1,2)之间，具体视情况而定。
松弛法的主题思想是将
乘上一个参数因子w来作为修正项，从而得到新的近似解。迭代公式可见如下：
上式子中的的计算，可见如下：
由此可得迭代的化简过程，如下：
按照上述式子计算Ax=b的近似解序列的方法，就被称之为松弛法，其中w为松弛因子。当w<1时称为低松弛；当w>1时称为超松弛；当w=1时，其实就是Gauss-Seidel迭代。
根据以上过程构造sor函数，MATLAB代码如下：
function y=sor(a,b,w,x0)
D=diag(diag(a)); %形成对角矩阵，其余元素为0
U=-triu(a,1);
L=-tril(a,-1);
M=(D-w*L)\((1-w)*D+w*U);
f=(D-w*L)\b*w;
y=M*x0+f;
n=1;
while norm(y-x0)>=1.0e-6
x0=y;
y=M*x0+f;
n=n+1;
end
n
end
例题5
设x0=0，精度为，w=1.103，利用SOR方法求解以下方程组。
解：
MATLAB代码如下：
clc;clear;
a=[10 -1 0;-1 10 -2;0 -2 10];
b=[9;7;6];
sor(a,b,1.103,[0;0;0])
%函数部分
function y=sor(a,b,w,x0)
D=diag(diag(a)); %形成对角矩阵，其余元素为0
U=-triu(a,1);
L=-tril(a,-1);
M=(D-w*L)\((1-w)*D+w*U);
f=(D-w*L)\b*w;
y=M*x0+f;
n=1;
while norm(y-x0)>=1.0e-6
x0=y;
y=M*x0+f;
n=n+1;
end
n
end运行结果：
n =
8
ans =
0.9958
0.9579
0.7916
六. 两步迭代法
当线性方程系数矩阵为对称正定时，还可以使用一种特殊的迭代法来解决：两步迭代法。迭代的公式，如下：
首先可得：
进一步推导可得：
根据以上计算过程，可以编写twostp()函数，MATLAB代码如下：
function y=twostp(a,b,x0)
D=diag(diag(a));
U=-triu(a,1);
L=-tril(a,-1);
G1=(D-L)\U;f1=(D-L)\b;
G2=(D-U)\L;f2=(D-U)\b;
y=G1*x0+f1;
y=G2*y+f2;
n=1;
while norm(y-x0)>=1.0e-6
x0=y;
y=G1*x0+f1;
y=G2*y+f2;
n=n+1;
end
n
end例题6
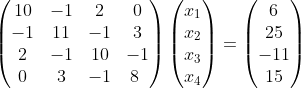
利用两步法，求解如下方程组：
解：
MATLAB代码如下：
clc;clear;
a=[10 -1 2 0;-1 11 -1 3;2 -1 10 3;0 3 -1 8];
b=[6;25;-11;15];
twostp(a,b,[0;0;0;0])
function y=twostp(a,b,x0)
D=diag(diag(a));
U=-triu(a,1);
L=-tril(a,-1);
G1=(D-L)\U;f1=(D-L)\b;
G2=(D-U)\L;f2=(D-U)\b;
y=G1*x0+f1;
y=G2*y+f2;
n=1;
while norm(y-x0)>=1.0e-6
x0=y;
y=G1*x0+f1;
y=G2*y+f2;
n=n+1;
end
n
end运行结果：
n =
7
ans =
1.0791
1.9824
-1.4044
0.9560