填充和跨度——【torch学习笔记】
卷积之填充和跨度
引用翻译:《动手学深度学习》
在上一节的例子中,我们用一个高度和宽度为3的输入和一个高度和宽度为2的卷积核来得到一个高度和宽度为2的输出。一般来说,假设输入的形状是nh × nw,卷积核的窗口形状是kh × kw,那么输出的形状将是(nh − kh + 1) × (nw − kw + 1)。因此,卷积层的输出形状是由输入的形状和卷积核窗的形状决定的。在一些情况下,我们可能想改变输出的维度。
-
多层卷积会减少边界上的可用信息,往往比我们想要的要多得多。如果我们从一个240x240像素的图像开始,10层5x5的卷积就会将图像减少到200x200像素,有效地切掉了30%的图像,同时也抹去了边界上任何有趣的东西。填充可以缓解这个问题。- 在某些情况下,我们希望大幅降低分辨率,例如,如果我们认为不需要这么高的输入维度,就把它减半。在这种情况下,我们可能想对输出进行子样化。Strides可以解决这个问题。
-
在某些情况下,我们希望提高分辨率,例如用于图像超分辨率或用于音频生成。同样地,strides也会来帮助我们。
-
在某些情况下,我们想把长度轻轻地增加到一个给定的大小(主要用于长度可变的句子或用于填充补丁)。填充(Padding)可以解决这个问题。
一、填充(Padding)
正如我们到目前为止所看到的,卷积是非常有用的。在边界上我们遇到了一个问题,那就是我们不断地失去像素。对于任何给定的卷积来说,这只是几个像素,但正如我们上面所讨论的那样,这就增加了。如果图像更大,事情就会更容易–我们可以简单地记录一个更大的图像。不幸的是,这不是我们在现实中得到的东西。解决这个问题的一个办法是在图像的边界周围增加额外的像素,从而增加图像的有效尺寸(额外的像素通常假设值为0)。在下图中,我们把3×3垫高,增加到5×5 (相当于在外面套了一层壳) 。然后相应的输出增加到4×4的矩阵。
图6.2:带填充的二维交叉相关。阴影部分是第一个输出元素所使用的输入和内核阵列元素。0×0 + 0×1 + 0×2 + 0×3 = 0.
一般来说,如果在高度的两边总共填充了ph行,在宽度的两边总共填充了pw 列,那么输出的形状将是(nh − kh + ph + 1) × (nw − kw + pw + 1),这意味着 输出的高度和宽度将分别增加 ph 和 pw
在许多情况下,我们希望设置ph = kh − 1 和 pw = kw − 1 ,使输入和输出具有相同的高度和宽度(正方形,长宽一致) 。这将使我们在构建网络时更容易预测每层的输出形状。
-
假设这里kh是奇数,我们将在高度的两边垫上ph /2行。
-
如果kh是偶数,一种可能性是在输入顶部垫上⌈ph /2⌉行,底部垫上⌊ph /2⌋行。
-
我们将以同样的方式对宽度的两边进行填充。
卷积神经网络经常使用具有奇数高度和宽度值的卷积核,如1、3、5和7,所以两边的填充行或列的数量是相同的。
对于任何二维数组X,假设其第i行和第j列的元素为X[i,j]。当两边的填充行数或列数相同,使输入和输出具有相同的高度和宽度时,我们知道输出Y[i,j]是通过输入和卷积核与以X[i,j]为中心的窗口的交叉相关来计算的。
在下面的例子中,我们创建了一个高度和宽度为3的二维卷积层,然后假设输入高度和宽度两边的填充数为1。给定一个高度和宽度为8的输入,我们发现输出的高度和宽度也为8。
import torch
import torch.nn as nn
# 我们定义了一个方便的函数来计算卷积层。这个函数初始化了卷积层的权重,并对输入和输出进行了相应的维度提升和降低
def comp_conv2d(conv2d, X):
# (1,1)表示批量大小和通道数量都是1
print('X变换前shape: ',X.shape)
X = X.reshape((1, 1) + X.shape)
print('X变换后shape: ',X.shape)
Y = conv2d(X) # 定义的卷积层
# 排除我们不感兴趣的前两个维度:批次和渠道
print('Y.shape[2:] : ',Y.shape[2:])
return Y.reshape(Y.shape[2:])
# 请注意,这里有1行或1列被填充在两边,所以总共有2行或2列被添加。
conv2d = nn.Conv2d(in_channels=1,out_channels=1,kernel_size=3,padding=1)
X = torch.rand(size=(10, 10)) # 传入的张量,数值可以取(8,8),(10,10)等,会根据输入的情况自动调整输入输出
comp_conv2d(conv2d, X).shape # 计算卷积后的结果
X变换前shape: torch.Size([10, 10])
X变换后shape: torch.Size([1, 1, 10, 10])
Y.shape[2:] : torch.Size([10, 10])
torch.Size([10, 10])
当卷积核的高度和宽度不同时,我们可以通过为高度和宽度设置不同的填充数,使输出和输入具有相同的高度和宽度。
若padding=(2, 1)随机取值时,输入输出维度会变得不一定一致.
如输入维度10 * 10,卷积核5 * 3,若不进行填充,则输出维度为 6*8,希望设置ph = kh − 1 和 pw = kw − 1 ,则ph = 5-1 = 4
这里 kh是奇数5,我们将在高度的两边垫上ph /2行。 此时ph/2 = 2
对于宽而言:
此时kw 是奇数3,则pw = 3-1 = 2,我们将在高度的两边垫上pw /2行。此时pw/2 = 1
则padding = (2,1)
# 在这里,我们使用一个高度为5,宽度为3的卷积核,高度和宽度两侧的填充数分别为2和2
# 输入维度10*10,卷积核5*3,若不进行填充,则输出维度为 6*8,
conv2d = nn.Conv2d(in_channels=1,out_channels=1, kernel_size=(5, 3), padding=(0, 0))
print('若不进行填充: ',comp_conv2d(conv2d, X).shape)
print('\n')
conv2d = nn.Conv2d(in_channels=1,out_channels=1, kernel_size=(5, 3), padding=(2, 1))
print('若填充(2,1): ',comp_conv2d(conv2d, X).shape)
print('\n')
conv2d = nn.Conv2d(in_channels=1,out_channels=1, kernel_size=(5, 3), padding=(2, 2))
print('若填充(2,2): ',comp_conv2d(conv2d, X).shape)
输出:
X变换前shape: torch.Size([10, 10])
X变换后shape: torch.Size([1, 1, 10, 10])
Y.shape[2:] : torch.Size([6, 8])
若不进行填充: torch.Size([6, 8])
X变换前shape: torch.Size([10, 10])
X变换后shape: torch.Size([1, 1, 10, 10])
Y.shape[2:] : torch.Size([10, 10])
若填充(2,1): torch.Size([10, 10])
X变换前shape: torch.Size([10, 10])
X变换后shape: torch.Size([1, 1, 10, 10])
Y.shape[2:] : torch.Size([10, 12])
若填充(2,2): torch.Size([10, 12])
二、跨度
当计算交叉相关时,卷积窗口从输入阵列的左上方开始,在输入阵列中从左到右、从上到下滑动。我们把每次滑动的行和列的数量称为跨度。
在当前的例子中,无论是高度还是宽度,stride都是1。我们也可以使用更大的跨度。下图显示了一个二维的交叉关联操作,垂直方向的跨度为3,水平方向为2。我们可以看到,当第一列的第二个元素被输出时,卷积窗口向下滑动了三行。当第一行的第二个元素被输出时,卷积窗口向右滑动了两列。当卷积窗口在输入时向右滑动两列时,没有输出,因为输入元素不能填满窗口(除非我们添加填充)。
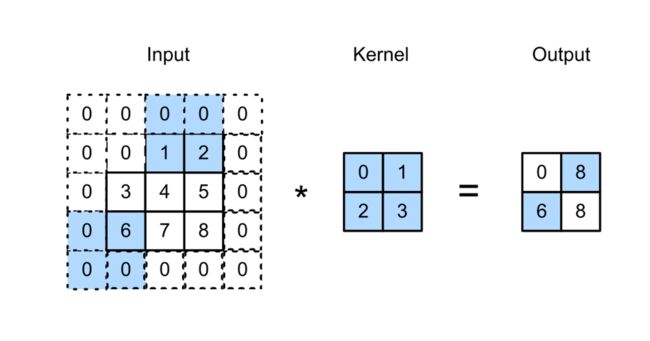
图6.3:高度和宽度的步长分别为3和2的交叉相关。阴影部分是输出元素和用于其计算的输入和核心阵列元素。0×0 + 0×1 + 1×2 + 2×3 = 8, 0×0 + 6×1 + 0×2 + 0×3 = 6.
一般来说,当高度的跨度为 sh,宽度的跨度为sw时,输出形状为(nh − kh + ph + sh ) / sh 和 (nw − kw + pw + sw ) / sw .
如果我们设定ph = kh − 1 和 pw = kw − 1,那么输出形状将简化为
(nh + sh − 1) / sh × (nw + sw − 1) / sw
结合步长后的计算方法:
再进一步说,如果输入的高度和宽度能被高度和宽度上的步长所除,那么输出的形状将是(nh / sh ) × (nw / sw ).。
下面,我们将高度和宽度的跨度都设为2,从而使输入的高度和宽度减半。
conv2d = nn.Conv2d(in_channels=1,out_channels=1, kernel_size=3, padding=1, stride=2)
print('stride=2:')
comp_conv2d(conv2d, X).shape
print('\n')
conv2d = nn.Conv2d(in_channels=1,out_channels=1, kernel_size=3, padding=1, stride=5)
print('stride=5:')
comp_conv2d(conv2d, X).shape
stride=2:
X变换前shape: torch.Size([10, 10])
X变换后shape: torch.Size([1, 1, 10, 10])
Y.shape[2:] : torch.Size([5, 5])
stride=5:
X变换前shape: torch.Size([10, 10])
X变换后shape: torch.Size([1, 1, 10, 10])
Y.shape[2:] : torch.Size([2, 2])
torch.Size([2, 2])
接下来,我们将看一个稍微复杂的例子:
当高度的跨度为 sh,宽度的跨度为sw时,输出形状为(nh − kh + ph + sh ) / sh 和 (nw − kw + pw + sw ) / sw .
即padding=(2, 1)时:
stride默认为1,
对于行:当stride取(3, 4)时,则是横向跨度为3,纵向跨度为4,即横向输入维度为10,其中 sh= 3,padding=2,则输出为(nh − kh + ph + sh ) / sh = (10-3+2+3)/3=4
对于列:纵向跨度为4,即纵向输入维度为10,其中 sw = 4,padding=1,则输出 为 (nw − kw + pw + sw ) / sw .=(10-5+1+4)/4 = 2.5—>2
conv2d = nn.Conv2d(in_channels=1,out_channels=1, kernel_size=(3, 5), padding=(2, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape
X变换前shape: torch.Size([10, 10])
X变换后shape: torch.Size([1, 1, 10, 10])
Y.shape[2:] : torch.Size([4, 2])
torch.Size([4, 2])
为了简洁起见,当输入高度和宽度两边的填充数分别为ph 和
pw 时,我们称之为填充数(ph , pw )。具体来说,当ph = pw = p时,填充数为p。
当高度和宽度上的跨度分别为sh 和 sw时,我们称跨度为(sh,sw)。具体来说,当sh = sw = s时,stride为s。默认情况下,padding为0,stride为1。在实践中,我们很少使用不均匀的stride或padding,即我们通常是 ph = pw 和 sh = sw .
三、摘要
-
Padding可以增加输出的高度和宽度。这通常被用来使输出的高度和宽度与输入的相同。
-
stride可以降低输出的分辨率,例如,将输出的高度和宽度降低到只有输入高度和宽度的1/n(n是大于1的整数)。
-
Padding和stride可以用来有效地调整数据的维度。
四、练习
-
或本节最后一个例子,用形状计算公式计算输出的形状,看是否与实验结果一致。
-
在本节的实验中尝试其他填充和跨度组合。
-
对于音频信号,2的步长对应于什么?
-
大于1的步长在计算上有什么好处。