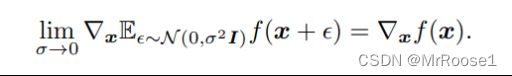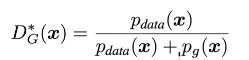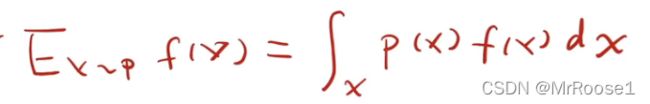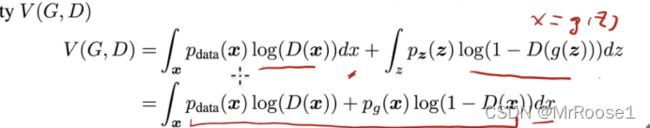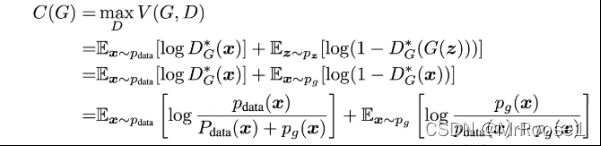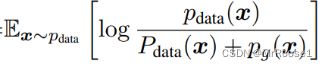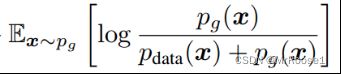GAN论文详细解读+思想

论文地址： [PDF] Generative Adversarial Nets | Semantic Scholar

注：由于这篇精读是之前总结在word中，里面公式不能直接copy到这里，我就直接截图了，省事但带来的问题是有个别公式截图被水印挡了一点，大家可以打开论文寻找相应的公式哈，很方便。

Intro

深度学习不仅仅是讲深度神经网络，它更多的是对整个数据分布的一个特征的表示。

深度学习在生成模式上做的比较差的原因：在最大化似然函数的时候，我们要对这个概率分布进行很多近似，近似会带来很多计算上的困难。因此GAN就是一个不需要近似函数且计算上更好的模型。

生成模型是一个MLP，输入是一个随机的噪音，MLP会把一个产生噪音的分布（通常是高斯分布）可以映射到任何一个我们想要去拟合的分布。如果判别模型也是MLP的情况下，我们就可以通过误差的反向传递，进而不需要通过像马尔科夫链一样来对一个分布进行复杂的采样，进而在计算上有优势。

Relat

作者发现之前的方法都是想办法构造出一个分布函数出来，然后把函数提供一些参数进行学习，这些参数通过最大化它的对数似然函数来做。但他的缺点就是在维度比较高的时候计算量很大。而GAN是通过学一个模型来近似分布。但缺点是他最后不知道分布长什么样子，但计算上比较容易。

 

作者后来发现对于f的期望求导等价于他对于f自己求导。这也是为什么我们通过误差的反向传递对GAN进行求解。

Adversarial nets

其中z是随机噪音向量，Pz是一个分布，θ都是需要学习的参数。的作用是将z输入然后产生一个x向量。的作用是将x向量输入，然后产生一个标量，这个标量是判断输入的x向量是否是真实值还是G生成值（越靠近真实值就越接近1，否则接近0），由于我们本身知道x是G生成的还是真实值，因此我们可以直接将数据标上真实值为1，G生成为0。然后采用一些数据训练一个二分类。

 

 

-----------------------------------------------------------------------------------------------------------------------------

这个是网络的目标函数，其中的x代表真实图片（向量），z代表噪因图片（随机向量）。

当D（辨别器）训练的很好的时候：D(x)=1，D(G(z)）=0，因此V(D,G)=0。

但往往D不可能训练的那么好，又因为有log，因此V(D,G)<0。我们在训练D的时候是看V(D,G)的,这也是为什么是要MAX~D的原因。而训练G的时候，只需要看即可，而G的目的是尽可能的让D给他生成的图片打分高，因此尽可能让D(G(z))趋向于1，1-D(G(z))趋向于0，因此log(1-D(G(z)))趋向于无穷小。这也是MIN~G的原因。

 

需要注意的是刚开始训练的时候G生产的图片效果很差，很容易让D(G(z))=0，这就导致了log(1-D(G(z)))=0，因此会导致对他求梯度再进行更新，会出现求不动的现象。因此作者建议训练G的时候求MAX~G，用log(D(G(z)))来求。

Theroretical

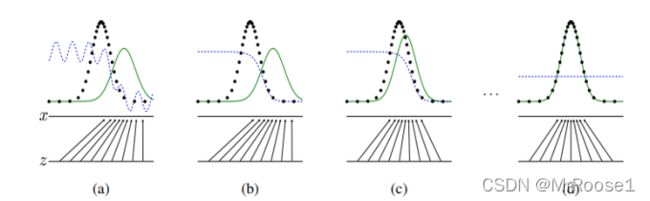
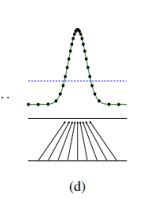
        绿色分布代表G生成的数据，黑色点阵分布代表真实数据，蓝色点阵分布代表D（判别器）的判别分布。

        (a)刚开始训练的时候由于D没有训练，所以蓝色点阵是无规则波动。此时G生成的数据在真实数据右侧，D根据真实值分高，G生成的数据分低原则进行学习，进而产生（b）的蓝色点阵分布。

         随后G训练更新参数（将生成的数据波峰左移）使其更接近真实值。然后再训练D，让其产生新的蓝色点阵分布。

        最后让G产生的数据分布与真实分布几乎重合，此时的D无法区分G产生的数据真假。

算法：

        先制造m个随机噪音向量，和m个从database中提取出来的真实数据

        随后开始将数据传入中开始计算辨别器的参数求梯度来更新辨别器，迭代k轮。 

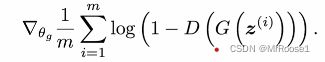        然后再制造m个随机噪音向量，然后把这m个随机噪音向量代入来更新生成器，计算机生成器的梯度进而更新生成器，迭代k轮。k是超参数。 

结论部分：

目标函数最优解：生成器学到的分布和真实数据的分布相等时 

最优解时：

当G固定住的时候，辨别器D的最优解是

Pdata(x)是指我把x放入真实数据分布中的数值是多少

Pg(x)是指我把x放入G学习到的分布中的数值是多少

Pdata和Pg分布数值都是0-1之间，因此D*G(x)的数值也在0-1之间。

当Pdata(x)==Pg(x)，那么D*G(x)=1/2。意味着辨别器D最优解的时候输出的值永远都是1/2，

表示这两个分布是完全重合，D无法区分开。

D是通过从两个分布（真实的数据和生成的数据）分别采样，用V(D,G)这个目标函数训练一个二分类的分类器，如果这个分类器的值都是1/2，就证明这两个分布完全重合了。

Two Sample Test方法：用来区分两块数据是不是来源于同一个分布。

下面开始证明(MAX~D)最优解公式：

---------------------------------------------------------------------------------------------------------------------------------

 

这个是求f(x)的期望公式，且x来自p的分布。

---------------------------------------------------------------------------------------------------------------------------------

 

上下公式通过x=g(z)来推导。

        又因为Pdata(x)和Pg(x)都是常量所以分别设为a，b，我们想要求D(x)，我们需要设D(x)为y，因此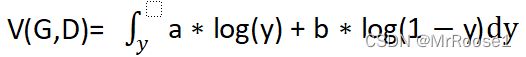，这个是一个凸函数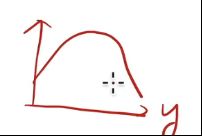，因此可以通过求导)来求得最大值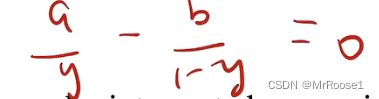因此y=a/(a+b)，因此也就是D(x)=Pdata(x)/{Pdata(x)+Pg(x)}。 

求完MAX~D，然后就该求MIN~G。

把D*G(x)带入V(D,G)中得C(G)，且C(G)求得最小值时Pdata(x)=Pg(x)

 

KL散度：公式：，其中x来自于p分布。 

KL散度的意义：已知p的情况下，需要多少个比特能把q表达出来。

且KL散度一定是大于等于0，且等于0时，q==p。

由于中

 

的log中的分子的范围都是0-1，而分母的范围都是0-2，而KL散度公式中分子分母范围都需要是0-1，因此需要将log中分母乘1/2，使分母的范围从0-2变成0-1。Log中分母乘1/2，分子也要乘1/2，因此相当于（－log2）*2=－log4。所以C(G)变为：

由于KL散度当等于0时才取到最小，所以Pdata=(Pdata+Pg)/2     Pg=(Pdata+Pg)/2  =>Pdata=Pg

GAN思想浅入：

GAN网络由generator（生成器）和discriminator（分辨器）组成。

所谓对抗的思想可以认为，generator是个做假钞的贩子，discriminator是个警察，第一次先将白纸给generator，生成一张假钞，然后discrimination进行检查（discrimination根据他所掌握真钞的某个特征来判断是否是假钞），每一轮刚开始检查的时候discrimination都没有发现是假钞，通过updata他的参数最终学会了真钞的其他某个特征，然后discrimination发现是假钞后，generator会updata他的参数。优化后第二轮generator继续生成一张假钞.....

  一张图片通过generator后是出来一张图片，而出来的图片通过discrimination后出来的是数值（数值越大，证明假钞越逼真）

Generator想要自己生成的假钞通过discrimination出来的分数越来越高，所以不断updata自己的参数，discrimination为了让自己能识别出是假钞（为了使，通过自己出来后的分数低而updata自己的参数）