【车间订单拣选优化】基于遗传优化的车间订单拣选优化matlab仿真
汽车生产需要进行上千个零件的组装,而主机厂采用柔性生产,对于每种零部件的需求呈现小批量,多频次的特点,而对于服务于主机厂的区域分拨中心,需要对主机厂的订单进行拣选配送,完成需求的响应。如果按订单先到先拣的方式,将导致拣货工作人员在巷道内行走距离增加,效率较低,订单分批是为了提高拣选作业效率,目标就是缩短拣货过程中行走距离和时间,降本增效。
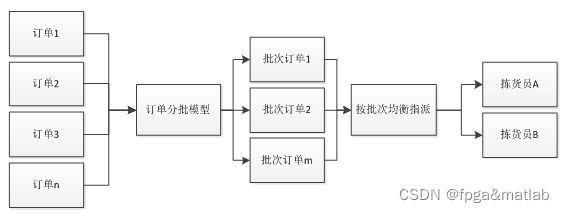
图1 订单拣选分批模型图
订单分批问题运用数学语言来表达是指把需要拣选的订单通过有效的模型进行分批,通过计算得出拣选的顺序从而使所求的目标函数实现最优。一般情况下建立的模型有两个优化目标:拣选行走距离最短或拣选行走时间最短,而这两个目标线性相关,距离的长短与行走时间呈正相关,因此本文建立以距离最短为目标的订单分批模型。
为了研究需要,同时基于问题的实际背景条件,本文对订单分批优化问题作出几点合理假设,具体如下:
(1)区域分拨中心的仓储为双区型仓库,仓库布局为平行排列的多层货架组成。相较于以往的单库型仓库,双区型更普遍于仓储运营,具有较好的实际意义,其仓库类型如图3-2;
(2)每张订单至少包含一个货品,且一张订单不可拆分为多个批次进行拣选;
(3)忽略货架高度所产生的距离,高度上的位移不算入拣选路径中;
(4)每个笼车的承重和容量规格相等,装载的货品容积和质量不超过限制条件;
(5)拣选单上的所有货物存储货位已知;
(6)紧急拉动的订单专人专车,不插入订单分批中;
(7)任意存储位置所储存的货物数量都能满足一次拣选要求;
(8)所有的拖车均为统一规格,移动速度与承载能力相同,拣选过程中速度一定,不考虑加速减速;
(9)拣选人员和拣选设备数量至少为一个,在运作过程中可能出现多个拣选设备同时拣选,故对于人员和设备不作要求
(10)拣选策略采用的为S型拣选路径
初始的参数全部放在程序的最上面
这些初始参数自己设置就好,可以设置,模拟不同的订单情况。
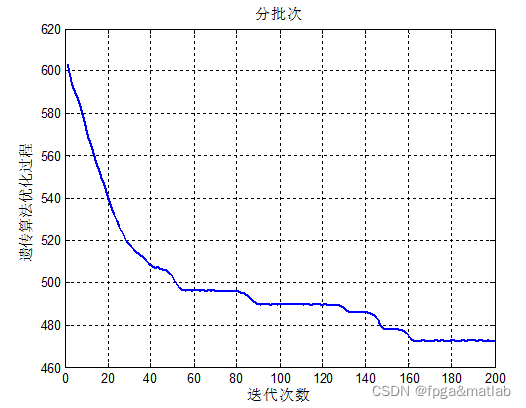
这个优化算法的收敛过程,
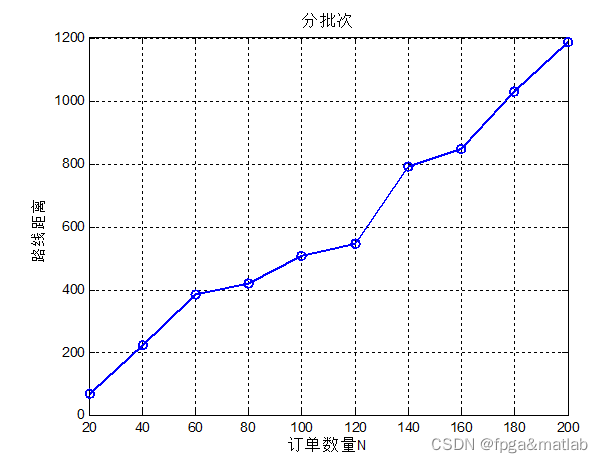
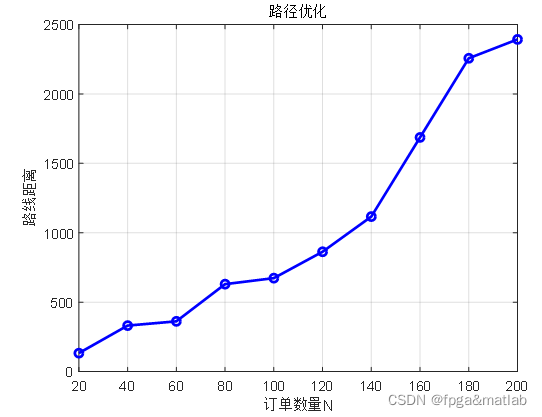
下面我们改变不同的订单数量,分析不同订单数量下的f的值的变换,仿真结果如下所示:
仿真结果如下所示:
这个优化算法的收敛过程,
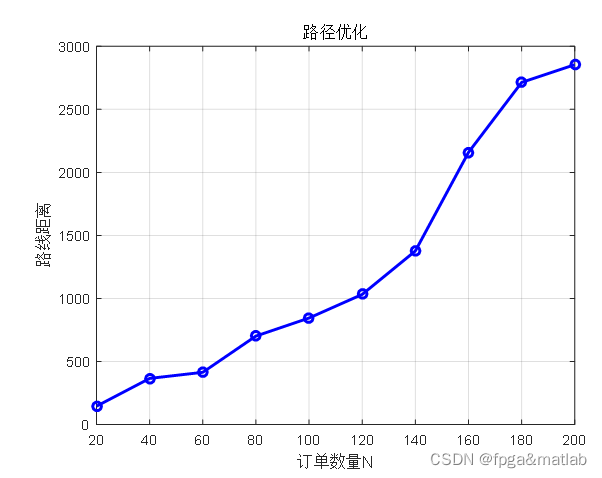
下面我们改变不同的订单数量,分析不同订单数量下的f的值的变换,仿真结果如下所示:
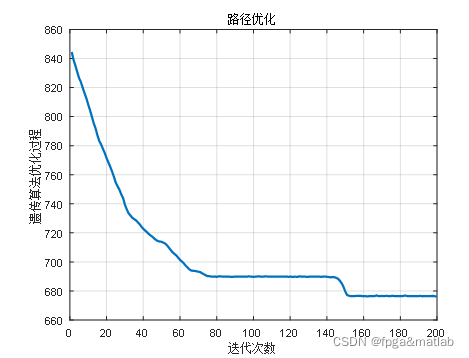
最后看一下,不优化情况下,直接进行处理,得到如下结果:
这里,采用的是第四章节的目标函数,不进行优化,获得的结果。从上面的结果对比可知,通过路径优化后的总体路径长度,优于直接处理的结果。
部分核心代码:
clc;
clear;
close all;
warning off;
addpath 'func\'
addpath 'GA_toolbox\'
load parameters.mat
rng('default');
types2 = unique(types);
global N;
global M;
global K;
global Z;
%订单总数,设置的时候,N*Z和M*K最好能够整除,这样计算速度快点,没小数
N = 100;
%拣选设备或人员数量
M = 4;
%批次
K = 1;%这里公式4.1没有K,所以直接设置K=1
%需拣订单零件品种数,如果某个订单品种小于Z,那么用0赋值
Z = 8;%这个变量就是每一个单子的最大种类,不能无限制大,否则仿真会非常慢
%随着设置Z个类型
for i = 1:N
rng(i);
xx = randperm(length(types2));
tmps = types2(xx)';
L = floor(Z*rand)+1;
if L==Z
Tget(1:Z,i) = [tmps(1:L)]';
else
Tget(1:Z,i) = [[tmps(1:L)]';zeros(Z-L,1)];
end
end
Tget2 = reshape(Tget,[1,Z*N]);
AS=[];
for i = 1:length(Tget2);
if Tget2(i)>0
indx = find(types==Tget2(i));
AS{i}=indx;
else
AS{i}=0;
end
end
rng(1);
%载货容积能力
Vmv = 10+2*rand(1,M);
Qmv = 100*Vmv;
rng('shuffle')
MAXGEN = 200;
NIND = 500;
Nums = N*Z; %
Chrom = crtbp(NIND,Nums*10);
%sh
Areas = [];
for i = 1:Nums
Areas = [Areas,[1;length(AS{i})]];
end
FieldD = [rep([10],[1,Nums]);Areas;rep([0;0;0;0],[1,Nums])];
gen = 0;
%计算对应的目标值
tmps = randperm(length(types));
X = tmps(1:Nums);%初始值
fobj = func_obj(X,Tget2,AS,Lmatrix,St,Et,V,Vcode,Mcode,Vmv,Qmv,types,POS);
E = fobj;
Js = E*ones(NIND,1);
Objv = (Js+eps);
gen = 0;
%%
while gen < MAXGEN;
gen
rng(gen);
Pe0 = 0.9999;
pe1 = 0.0001;
FitnV=ranking(Objv);
Selch=select('sus',Chrom,FitnV);
Selch=recombin('xovsp', Selch,Pe0);
Selch=mut( Selch,pe1);
phen1=bs2rv(Selch,FieldD);
for a=1:1:NIND
X1 = round(phen1(a,:));
X11 = [];
for j = 1:length(AS)
if AS{j} == 0
X11 = [X11,0];
else
X11 = [X11,AS{j}(X1(j))];
end
end
%计算对应的目标值
fobj = func_obj(X11,Tget2,AS,Lmatrix,St,Et,V,Vcode,Mcode,Vmv,Qmv,types,POS);
E = fobj;
JJ(a,1) = E;
end
Objvsel=(JJ);
[Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);
gen=gen+1;
%保存参数收敛过程和误差收敛过程以及函数值拟合结论
Error(gen) = mean(JJ);
end
figure;
plot(Error,'linewidth',2);
grid on
xlabel('迭代次数');
ylabel('遗传算法优化过程');
save R2a.mat Error
A06-59